Variational Encoder-Decoders for Learning Latent Representations of Physical Systems

We present a deep-learning Variational Encoder-Decoder (VED) framework for learning data-driven low-dimensional representations of the relationship between high-dimensional parameters of a physical system and the system's high-dimensional observable response. The framework consists of two deep learning-based probabilistic transformations: An encoder mapping parameters to latent codes and a decoder mapping latent codes to the observable response. The hyperparameters of these transformations are identified by maximizing a variational lower bound on the log-conditional distribution of the observable response given parameters. To promote the disentanglement of latent codes, we equip this variational loss with a penalty on the off-diagonal entries of the aggregate distribution covariance of codes. This regularization penalty encourages the pushforward of a standard Gaussian distribution of latent codes to approximate the marginal distribution of the observable response. Using the proposed framework we successfully model the hydraulic pressure response at observation wells of a groundwater flow model as a function of its discrete log-hydraulic transmissivity field. Compared to the canonical correlation analysis encoding, the VED model achieves a lower-dimensional latent representation, with as low as $r = 50$ latent dimensions without a significant loss of reconstruction accuracy. We explore the impact of regularization on model performance, finding that KL-divergence and covariance regularization improve feature disentanglement in latent space while maintaining reconstruction accuracy. Furthermore, we evaluate the generative capabilities of the regularized model by decoding random Gaussian noise, revealing that tuning both $\beta$ and $\lambda$ parameters enhances the quality of the generated observable response data.

Conditional Korhunen-Loéve regression model with Basis Adaptation for high-dimensional problems: uncertainty quantification and inverse modeling

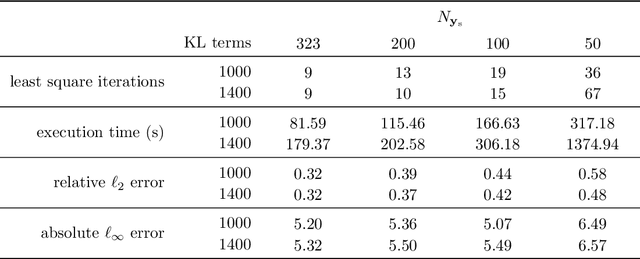
We propose a methodology for improving the accuracy of surrogate models of the observable response of physical systems as a function of the systems' spatially heterogeneous parameter fields with applications to uncertainty quantification and parameter estimation in high-dimensional problems. Practitioners often formulate finite-dimensional representations of spatially heterogeneous parameter fields using truncated unconditional Karhunen-Lo\'{e}ve expansions (KLEs) for a certain choice of unconditional covariance kernel and construct surrogate models of the observable response with respect to the random variables in the KLE. When direct measurements of the parameter fields are available, we propose improving the accuracy of these surrogate models by representing the parameter fields via conditional Karhunen-Lo\'{e}ve expansions (CKLEs). CKLEs are constructed by conditioning the covariance kernel of the unconditional expansion on the direct measurements via Gaussian process regression and then truncating the corresponding KLE. We apply the proposed methodology to constructing surrogate models via the Basis Adaptation (BA) method of the stationary hydraulic head response, measured at spatially discrete observation locations, of a groundwater flow model of the Hanford Site, as a function of the 1,000-dimensional representation of the model's log-transmissivity field. We find that BA surrogate models of the hydraulic head based on CKLEs are more accurate than BA surrogate models based on unconditional expansions for forward uncertainty quantification tasks. Furthermore, we find that inverse estimates of the hydraulic transmissivity field computed using CKLE-based BA surrogate models are more accurate than those computed using unconditional BA surrogate models.

Gaussian process regression and conditional Karhunen-Loéve models for data assimilation in inverse problems

We present a model inversion algorithm, CKLEMAP, for data assimilation and parameter estimation in partial differential equation models of physical systems with spatially heterogeneous parameter fields. These fields are approximated using low-dimensional conditional Karhunen-Lo\'{e}ve expansions, which are constructed using Gaussian process regression models of these fields trained on the parameters' measurements. We then assimilate measurements of the state of the system and compute the maximum a posteriori estimate of the CKLE coefficients by solving a nonlinear least-squares problem. When solving this optimization problem, we efficiently compute the Jacobian of the vector objective by exploiting the sparsity structure of the linear system of equations associated with the forward solution of the physics problem. The CKLEMAP method provides better scalability compared to the standard MAP method. In the MAP method, the number of unknowns to be estimated is equal to the number of elements in the numerical forward model. On the other hand, in CKLEMAP, the number of unknowns (CKLE coefficients) is controlled by the smoothness of the parameter field and the number of measurements, and is in general much smaller than the number of discretization nodes, which leads to a significant reduction of computational cost with respect to the standard MAP method. To show its advantage in scalability, we apply CKLEMAP to estimate the transmissivity field in a two-dimensional steady-state subsurface flow model of the Hanford Site by assimilating synthetic measurements of transmissivity and hydraulic head. We find that the execution time of CKLEMAP scales nearly linearly as $N^{1.33}$, where $N$ is the number of discretization nodes, while the execution time of standard MAP scales as $N^{2.91}$. The CKLEMAP method improved execution time without sacrificing accuracy when compared to the standard MAP.

Physics-Informed Machine Learning Method for Large-Scale Data Assimilation Problems

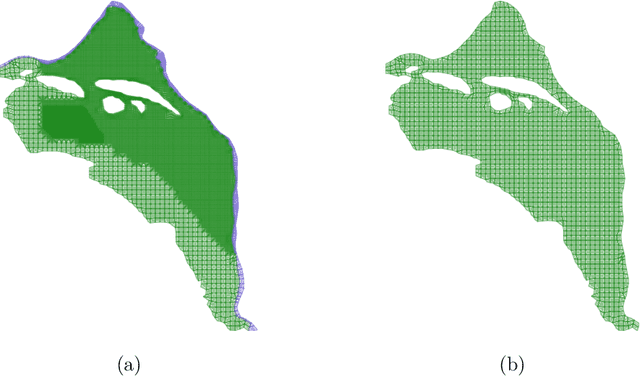
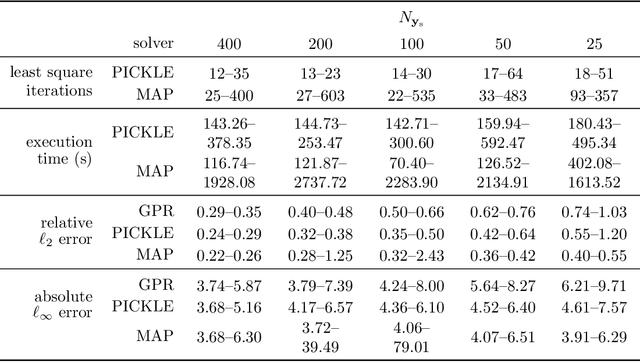
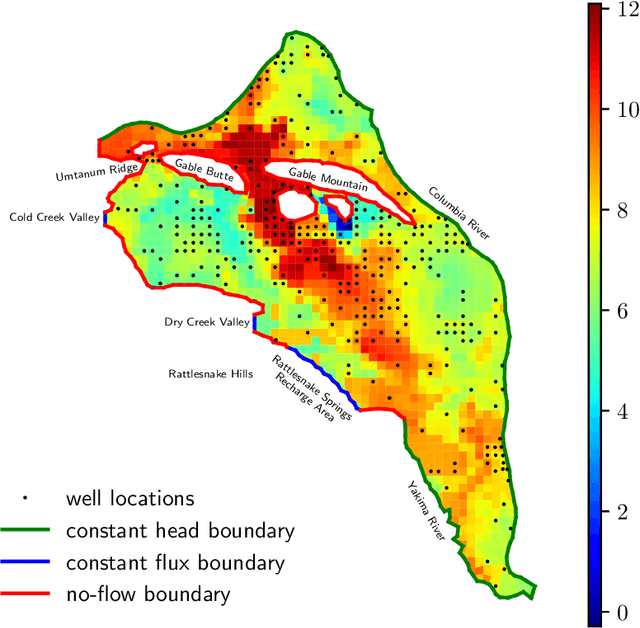
We develop a physics-informed machine learning approach for large-scale data assimilation and parameter estimation and apply it for estimating transmissivity and hydraulic head in the two-dimensional steady-state subsurface flow model of the Hanford Site given synthetic measurements of said variables. In our approach, we extend the physics-informed conditional Karhunen-Lo\'{e}ve expansion (PICKLE) method for modeling subsurface flow with unknown flux (Neumann) and varying head (Dirichlet) boundary conditions. We demonstrate that the PICKLE method is comparable in accuracy with the standard maximum a posteriori (MAP) method, but is significantly faster than MAP for large-scale problems. Both methods use a mesh to discretize the computational domain. In MAP, the parameters and states are discretized on the mesh; therefore, the size of the MAP parameter estimation problem directly depends on the mesh size. In PICKLE, the mesh is used to evaluate the residuals of the governing equation, while the parameters and states are approximated by the truncated conditional Karhunen-Lo\'{e}ve expansions with the number of parameters controlled by the smoothness of the parameter and state fields, and not by the mesh size. For a considered example, we demonstrate that the computational cost of PICKLE increases near linearly (as $N_{FV}^{1.15}$) with the number of grid points $N_{FV}$, while that of MAP increases much faster as $N_{FV}^{3.28}$. We demonstrated that once trained for one set of Dirichlet boundary conditions (i.e., one river stage), the PICKLE method provides accurate estimates of the hydraulic head for any value of the Dirichlet boundary conditions (i.e., for any river stage).