Lorenz System State Stability Identification using Neural Networks
Paper and Code
Jun 16, 2021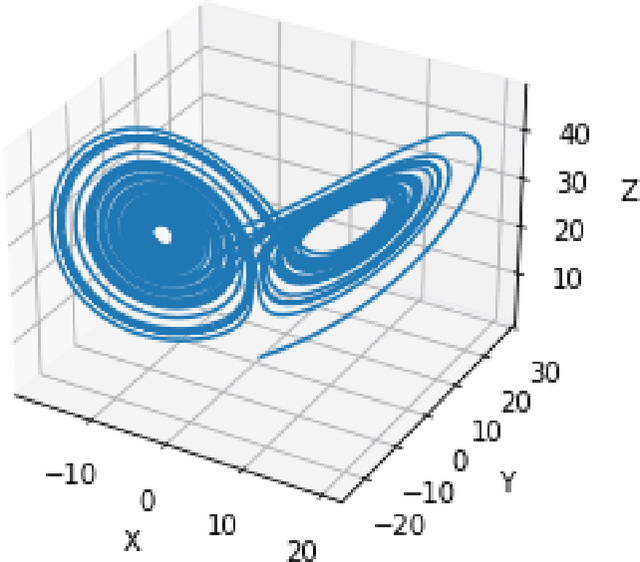
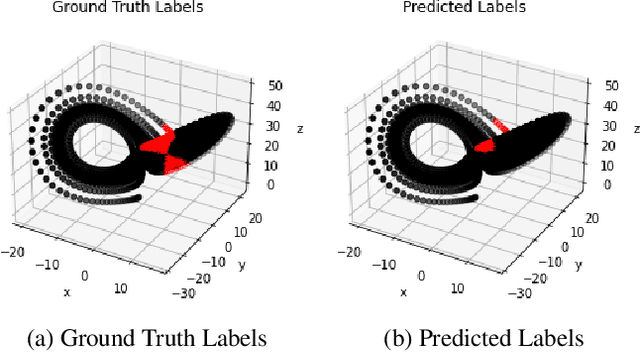
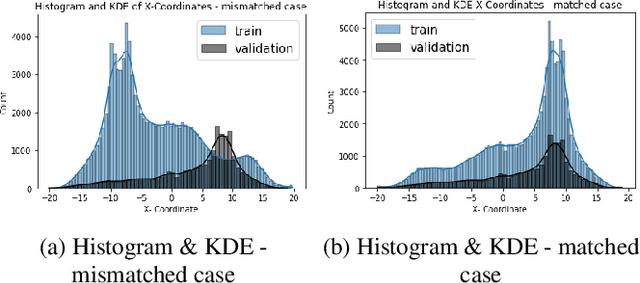
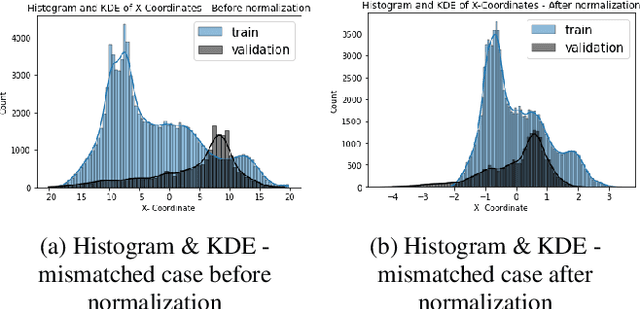
Nonlinear dynamical systems such as Lorenz63 equations are known to be chaotic in nature and sensitive to initial conditions. As a result, a small perturbation in the initial conditions results in deviation in state trajectory after a few time steps. The algorithms and computational resources needed to accurately identify the system states vary depending on whether the solution is in transition region or not. We refer to the transition and non-transition regions as unstable and stable regions respectively. We label a system state to be stable if it's immediate past and future states reside in the same regime. However, at a given time step we don't have the prior knowledge about whether system is in stable or unstable region. In this paper, we develop and train a feed forward (multi-layer perceptron) Neural Network to classify the system states of a Lorenz system as stable and unstable. We pose this task as a supervised learning problem where we train the neural network on Lorenz system which have states labeled as stable or unstable. We then test the ability of the neural network models to identify the stable and unstable states on a different Lorenz system that is generated using different initial conditions. We also evaluate the classification performance in the mismatched case i.e., when the initial conditions for training and validation data are sampled from different intervals. We show that certain normalization schemes can greatly improve the performance of neural networks in especially these mismatched scenarios. The classification framework developed in the paper can be a preprocessor for a larger context of sequential decision making framework where the decision making is performed based on observed stable or unstable states.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge