Estimating Exposure to Information on Social Networks
Paper and Code
Jul 13, 2022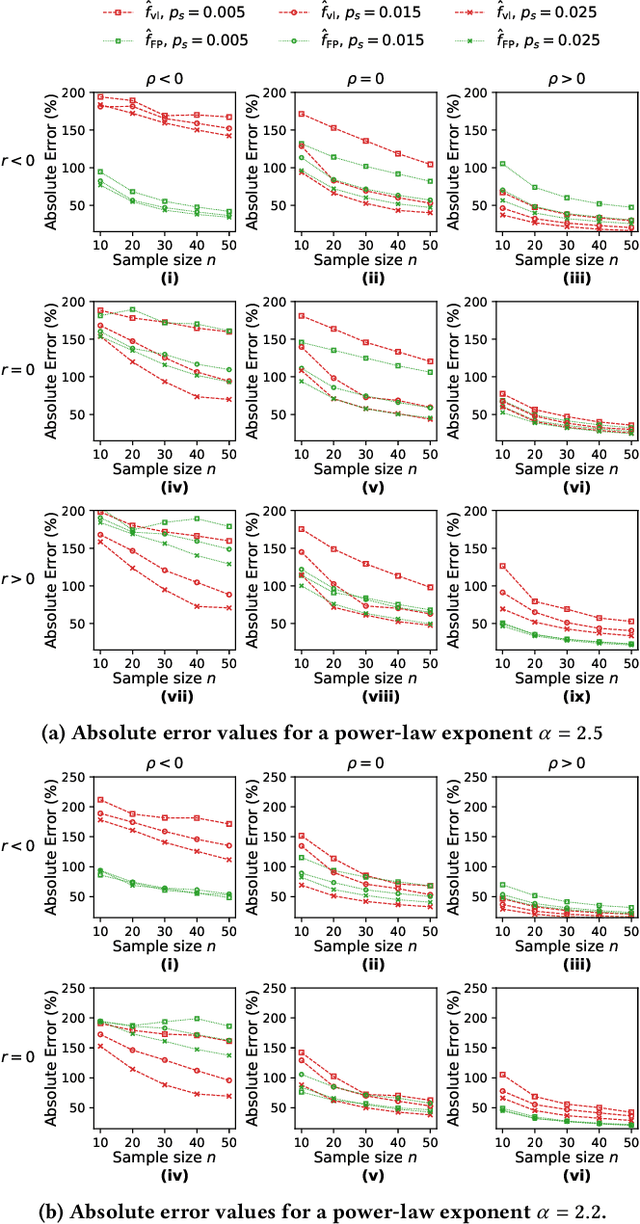
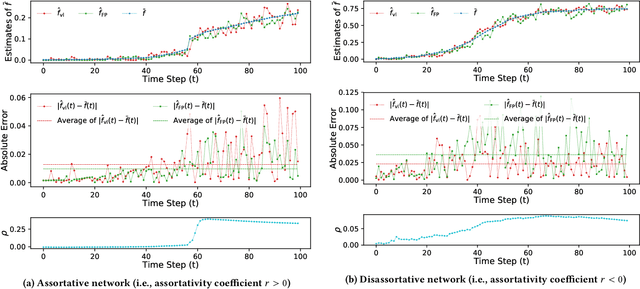
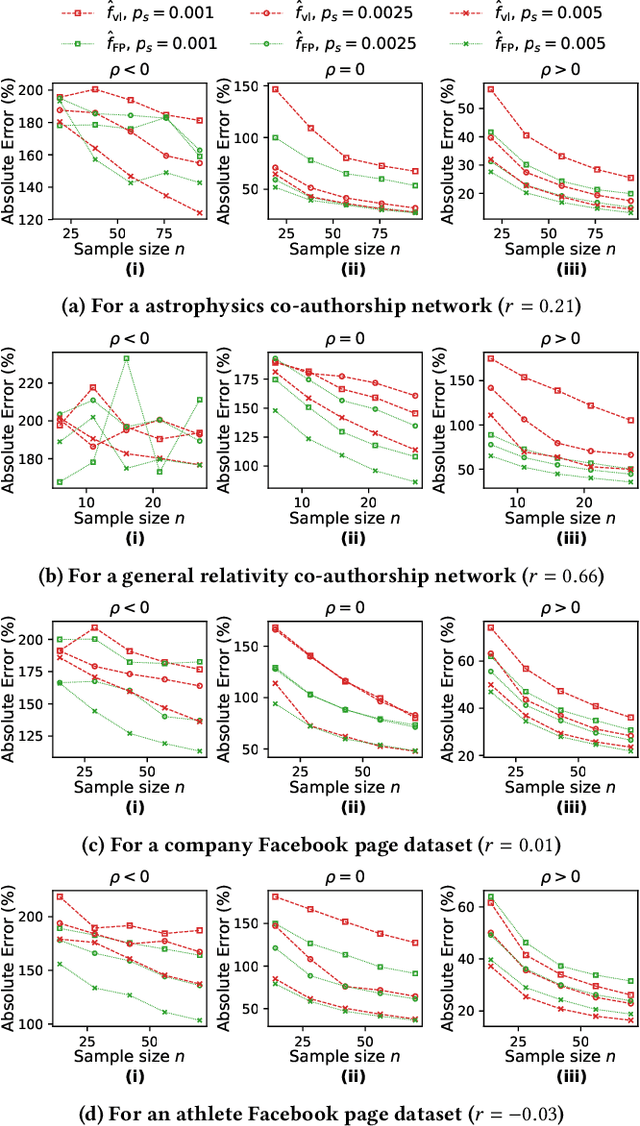
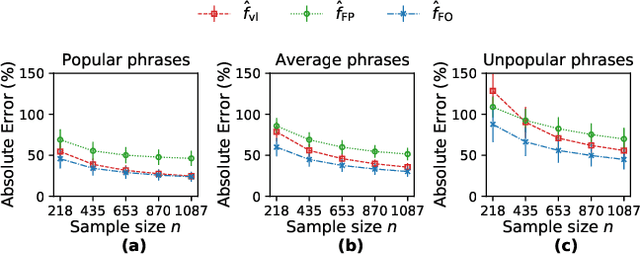
This paper considers the problem of estimating exposure to information in a social network. Given a piece of information (e.g., a URL of a news article on Facebook, a hashtag on Twitter), our aim is to find the fraction of people on the network who have been exposed to it. The exact value of exposure to a piece of information is determined by two features: the structure of the underlying social network and the set of people who shared the piece of information. Often, both features are not publicly available (i.e., access to the two features is limited only to the internal administrators of the platform) and difficult to be estimated from data. As a solution, we propose two methods to estimate the exposure to a piece of information in an unbiased manner: a vanilla method which is based on sampling the network uniformly and a method which non-uniformly samples the network motivated by the Friendship Paradox. We provide theoretical results which characterize the conditions (in terms of properties of the network and the piece of information) under which one method outperforms the other. Further, we outline extensions of the proposed methods to dynamic information cascades (where the exposure needs to be tracked in real-time). We demonstrate the practical feasibility of the proposed methods via experiments on multiple synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge