Memory Matters More: Event-Centric Memory as a Logic Map for Agent Searching and Reasoning

Large language models (LLMs) are increasingly deployed as intelligent agents that reason, plan, and interact with their environments. To effectively scale to long-horizon scenarios, a key capability for such agents is a memory mechanism that can retain, organize, and retrieve past experiences to support downstream decision-making. However, most existing approaches organize and store memories in a flat manner and rely on simple similarity-based retrieval techniques. Even when structured memory is introduced, existing methods often struggle to explicitly capture the logical relationships among experiences or memory units. Moreover, memory access is largely detached from the constructed structure and still depends on shallow semantic retrieval, preventing agents from reasoning logically over long-horizon dependencies. In this work, we propose CompassMem, an event-centric memory framework inspired by Event Segmentation Theory. CompassMem organizes memory as an Event Graph by incrementally segmenting experiences into events and linking them through explicit logical relations. This graph serves as a logic map, enabling agents to perform structured and goal-directed navigation over memory beyond superficial retrieval, progressively gathering valuable memories to support long-horizon reasoning. Experiments on LoCoMo and NarrativeQA demonstrate that CompassMem consistently improves both retrieval and reasoning performance across multiple backbone models.

Memory in the Age of AI Agents

Memory has emerged, and will continue to remain, a core capability of foundation model-based agents. As research on agent memory rapidly expands and attracts unprecedented attention, the field has also become increasingly fragmented. Existing works that fall under the umbrella of agent memory often differ substantially in their motivations, implementations, and evaluation protocols, while the proliferation of loosely defined memory terminologies has further obscured conceptual clarity. Traditional taxonomies such as long/short-term memory have proven insufficient to capture the diversity of contemporary agent memory systems. This work aims to provide an up-to-date landscape of current agent memory research. We begin by clearly delineating the scope of agent memory and distinguishing it from related concepts such as LLM memory, retrieval augmented generation (RAG), and context engineering. We then examine agent memory through the unified lenses of forms, functions, and dynamics. From the perspective of forms, we identify three dominant realizations of agent memory, namely token-level, parametric, and latent memory. From the perspective of functions, we propose a finer-grained taxonomy that distinguishes factual, experiential, and working memory. From the perspective of dynamics, we analyze how memory is formed, evolved, and retrieved over time. To support practical development, we compile a comprehensive summary of memory benchmarks and open-source frameworks. Beyond consolidation, we articulate a forward-looking perspective on emerging research frontiers, including memory automation, reinforcement learning integration, multimodal memory, multi-agent memory, and trustworthiness issues. We hope this survey serves not only as a reference for existing work, but also as a conceptual foundation for rethinking memory as a first-class primitive in the design of future agentic intelligence.

Learning from a Generative Oracle: Domain Adaptation for Restoration

Pre-trained image restoration models often fail on real-world, out-of-distribution degradations due to significant domain gaps. Adapting to these unseen domains is challenging, as out-of-distribution data lacks ground truth, and traditional adaptation methods often require complex architectural changes. We propose LEGO (Learning from a Generative Oracle), a practical three-stage framework for post-training domain adaptation without paired data. LEGO converts this unsupervised challenge into a tractable pseudo-supervised one. First, we obtain initial restorations from the pre-trained model. Second, we leverage a frozen, large-scale generative oracle to refine these estimates into high-quality pseudo-ground-truths. Third, we fine-tune the original model using a mixed-supervision strategy combining in-distribution data with these new pseudo-pairs. This approach adapts the model to the new distribution without sacrificing its original robustness or requiring architectural modifications. Experiments demonstrate that LEGO effectively bridges the domain gap, significantly improving performance on diverse real-world benchmarks.

Multimodal Diffusion Bridge with Attention-Based SAR Fusion for Satellite Image Cloud Removal

Deep learning has achieved some success in addressing the challenge of cloud removal in optical satellite images, by fusing with synthetic aperture radar (SAR) images. Recently, diffusion models have emerged as powerful tools for cloud removal, delivering higher-quality estimation by sampling from cloud-free distributions, compared to earlier methods. However, diffusion models initiate sampling from pure Gaussian noise, which complicates the sampling trajectory and results in suboptimal performance. Also, current methods fall short in effectively fusing SAR and optical data. To address these limitations, we propose Diffusion Bridges for Cloud Removal, DB-CR, which directly bridges between the cloudy and cloud-free image distributions. In addition, we propose a novel multimodal diffusion bridge architecture with a two-branch backbone for multimodal image restoration, incorporating an efficient backbone and dedicated cross-modality fusion blocks to effectively extract and fuse features from synthetic aperture radar (SAR) and optical images. By formulating cloud removal as a diffusion-bridge problem and leveraging this tailored architecture, DB-CR achieves high-fidelity results while being computationally efficient. We evaluated DB-CR on the SEN12MS-CR cloud-removal dataset, demonstrating that it achieves state-of-the-art results.

A Self-supervised Diffusion Bridge for MRI Reconstruction

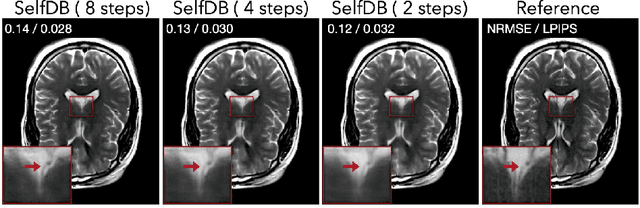
Diffusion bridges (DBs) are a class of diffusion models that enable faster sampling by interpolating between two paired image distributions. Training traditional DBs for image reconstruction requires high-quality reference images, which limits their applicability to settings where such references are unavailable. We propose SelfDB as a novel self-supervised method for training DBs directly on available noisy measurements without any high-quality reference images. SelfDB formulates the diffusion process by further sub-sampling the available measurements two additional times and training a neural network to reverse the corresponding degradation process by using the available measurements as the training targets. We validate SelfDB on compressed sensing MRI, showing its superior performance compared to the denoising diffusion models.

Plug-and-Play Priors as a Score-Based Method

Plug-and-play (PnP) methods are extensively used for solving imaging inverse problems by integrating physical measurement models with pre-trained deep denoisers as priors. Score-based diffusion models (SBMs) have recently emerged as a powerful framework for image generation by training deep denoisers to represent the score of the image prior. While both PnP and SBMs use deep denoisers, the score-based nature of PnP is unexplored in the literature due to its distinct origins rooted in proximal optimization. This letter introduces a novel view of PnP as a score-based method, a perspective that enables the re-use of powerful SBMs within classical PnP algorithms without retraining. We present a set of mathematical relationships for adapting popular SBMs as priors within PnP. We show that this approach enables a direct comparison between PnP and SBM-based reconstruction methods using the same neural network as the prior. Code is available at https://github.com/wustl-cig/score_pnp.

ADOBI: Adaptive Diffusion Bridge For Blind Inverse Problems with Application to MRI Reconstruction

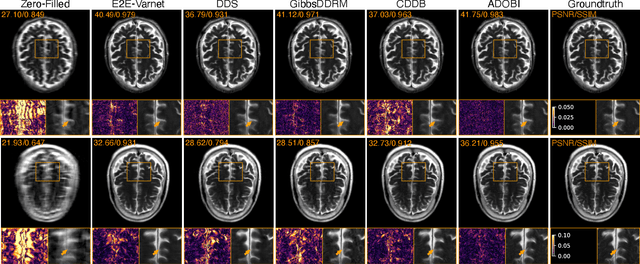
Diffusion bridges (DB) have emerged as a promising alternative to diffusion models for imaging inverse problems, achieving faster sampling by directly bridging low- and high-quality image distributions. While incorporating measurement consistency has been shown to improve performance, existing DB methods fail to maintain this consistency in blind inverse problems, where the forward model is unknown. To address this limitation, we introduce ADOBI (Adaptive Diffusion Bridge for Inverse Problems), a novel framework that adaptively calibrates the unknown forward model to enforce measurement consistency throughout sampling iterations. Our adaptation strategy allows ADOBI to achieve high-quality parallel magnetic resonance imaging (PMRI) reconstruction in only 5-10 steps. Our numerical results show that ADOBI consistently delivers state-of-the-art performance, and further advances the Pareto frontier for the perception-distortion trade-off.

Stochastic Deep Restoration Priors for Imaging Inverse Problems

Deep neural networks trained as image denoisers are widely used as priors for solving imaging inverse problems. While Gaussian denoising is thought sufficient for learning image priors, we show that priors from deep models pre-trained as more general restoration operators can perform better. We introduce Stochastic deep Restoration Priors (ShaRP), a novel method that leverages an ensemble of such restoration models to regularize inverse problems. ShaRP improves upon methods using Gaussian denoiser priors by better handling structured artifacts and enabling self-supervised training even without fully sampled data. We prove ShaRP minimizes an objective function involving a regularizer derived from the score functions of minimum mean square error (MMSE) restoration operators, and theoretically analyze its convergence. Empirically, ShaRP achieves state-of-the-art performance on tasks such as magnetic resonance imaging reconstruction and single-image super-resolution, surpassing both denoiser-and diffusion-model-based methods without requiring retraining.

DiffGEPCI: 3D MRI Synthesis from mGRE Signals using 2.5D Diffusion Model

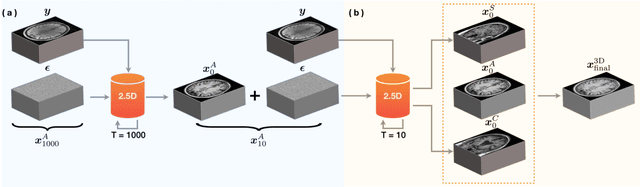
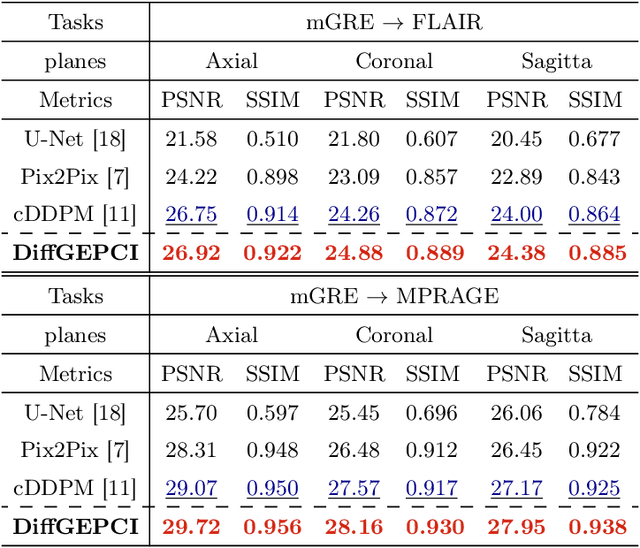
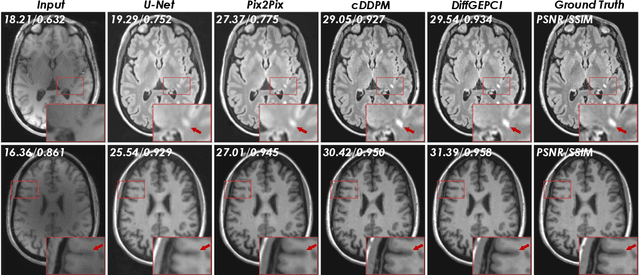
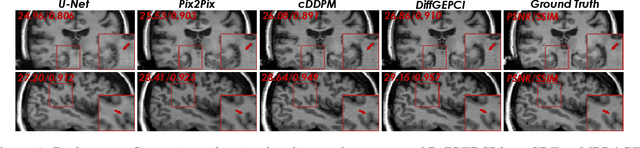
We introduce a new framework called DiffGEPCI for cross-modality generation in magnetic resonance imaging (MRI) using a 2.5D conditional diffusion model. DiffGEPCI can synthesize high-quality Fluid Attenuated Inversion Recovery (FLAIR) and Magnetization Prepared-Rapid Gradient Echo (MPRAGE) images, without acquiring corresponding measurements, by leveraging multi-Gradient-Recalled Echo (mGRE) MRI signals as conditional inputs. DiffGEPCI operates in a two-step fashion: it initially estimates a 3D volume slice-by-slice using the axial plane and subsequently applies a refinement algorithm (referred to as 2.5D) to enhance the quality of the coronal and sagittal planes. Experimental validation on real mGRE data shows that DiffGEPCI achieves excellent performance, surpassing generative adversarial networks (GANs) and traditional diffusion models.

A Structured Pruning Algorithm for Model-based Deep Learning

There is a growing interest in model-based deep learning (MBDL) for solving imaging inverse problems. MBDL networks can be seen as iterative algorithms that estimate the desired image using a physical measurement model and a learned image prior specified using a convolutional neural net (CNNs). The iterative nature of MBDL networks increases the test-time computational complexity, which limits their applicability in certain large-scale applications. We address this issue by presenting structured pruning algorithm for model-based deep learning (SPADE) as the first structured pruning algorithm for MBDL networks. SPADE reduces the computational complexity of CNNs used within MBDL networks by pruning its non-essential weights. We propose three distinct strategies to fine-tune the pruned MBDL networks to minimize the performance loss. Each fine-tuning strategy has a unique benefit that depends on the presence of a pre-trained model and a high-quality ground truth. We validate SPADE on two distinct inverse problems, namely compressed sensing MRI and image super-resolution. Our results highlight that MBDL models pruned by SPADE can achieve substantial speed up in testing time while maintaining competitive performance.