ADOBI: Adaptive Diffusion Bridge For Blind Inverse Problems with Application to MRI Reconstruction

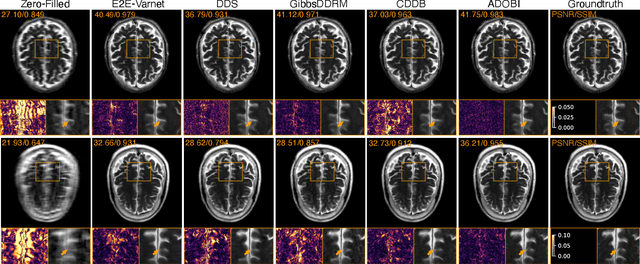
Diffusion bridges (DB) have emerged as a promising alternative to diffusion models for imaging inverse problems, achieving faster sampling by directly bridging low- and high-quality image distributions. While incorporating measurement consistency has been shown to improve performance, existing DB methods fail to maintain this consistency in blind inverse problems, where the forward model is unknown. To address this limitation, we introduce ADOBI (Adaptive Diffusion Bridge for Inverse Problems), a novel framework that adaptively calibrates the unknown forward model to enforce measurement consistency throughout sampling iterations. Our adaptation strategy allows ADOBI to achieve high-quality parallel magnetic resonance imaging (PMRI) reconstruction in only 5-10 steps. Our numerical results show that ADOBI consistently delivers state-of-the-art performance, and further advances the Pareto frontier for the perception-distortion trade-off.

Stochastic Deep Restoration Priors for Imaging Inverse Problems

Deep neural networks trained as image denoisers are widely used as priors for solving imaging inverse problems. While Gaussian denoising is thought sufficient for learning image priors, we show that priors from deep models pre-trained as more general restoration operators can perform better. We introduce Stochastic deep Restoration Priors (ShaRP), a novel method that leverages an ensemble of such restoration models to regularize inverse problems. ShaRP improves upon methods using Gaussian denoiser priors by better handling structured artifacts and enabling self-supervised training even without fully sampled data. We prove ShaRP minimizes an objective function involving a regularizer derived from the score functions of minimum mean square error (MMSE) restoration operators, and theoretically analyze its convergence. Empirically, ShaRP achieves state-of-the-art performance on tasks such as magnetic resonance imaging reconstruction and single-image super-resolution, surpassing both denoiser-and diffusion-model-based methods without requiring retraining.