Closed-Form Approximation of the Total Variation Proximal Operator

Total variation (TV) is a widely used function for regularizing imaging inverse problems that is particularly appropriate for images whose underlying structure is piecewise constant. TV regularized optimization problems are typically solved using proximal methods, but the way in which they are applied is constrained by the absence of a closed-form expression for the proximal operator of the TV function. A closed-form approximation of the TV proximal operator has previously been proposed, but its accuracy was not theoretically explored in detail. We address this gap by making several new theoretical contributions, proving that the approximation leads to a proximal operator of some convex function, that it always decreases the TV function, and that its error can be fully characterized and controlled with its scaling parameter. We experimentally validate our theoretical results on image denoising and sparse-view computed tomography (CT) image reconstruction.

TVCondNet: A Conditional Denoising Neural Network for NMR Spectroscopy

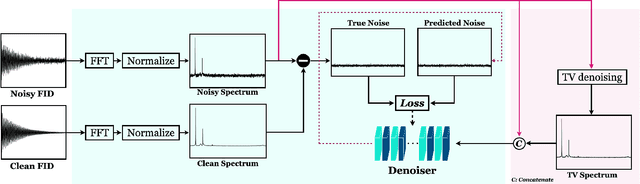
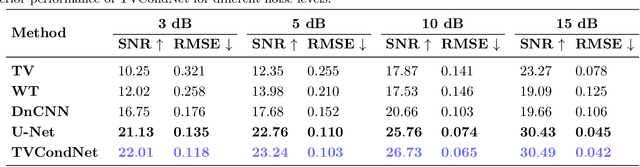
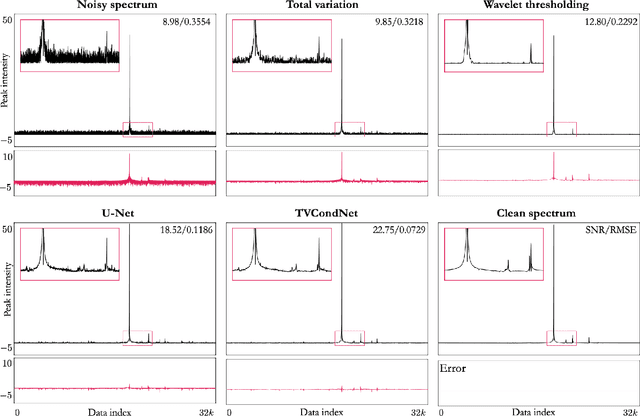
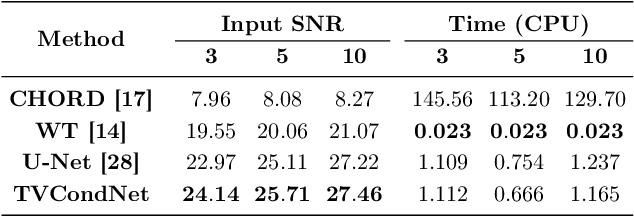
Nuclear Magnetic Resonance (NMR) spectroscopy is a widely-used technique in the fields of bio-medicine, chemistry, and biology for the analysis of chemicals and proteins. The signals from NMR spectroscopy often have low signal-to-noise ratio (SNR) due to acquisition noise, which poses significant challenges for subsequent analysis. Recent work has explored the potential of deep learning (DL) for NMR denoising, showing significant performance gains over traditional methods such as total variation (TV) denoising. This paper shows that the performance of DL denoising for NMR can be further improved by combining data-driven training with traditional TV denoising. The proposed TVCondNet method outperforms both traditional TV and DL methods by including the TV solution as a condition during DL training. Our validation on experimentally collected NMR data shows the superior denoising performance and faster inference speed of TVCondNet compared to existing methods.

Overcoming Distribution Shifts in Plug-and-Play Methods with Test-Time Training

Plug-and-Play Priors (PnP) is a well-known class of methods for solving inverse problems in computational imaging. PnP methods combine physical forward models with learned prior models specified as image denoisers. A common issue with the learned models is that of a performance drop when there is a distribution shift between the training and testing data. Test-time training (TTT) was recently proposed as a general strategy for improving the performance of learned models when training and testing data come from different distributions. In this paper, we propose PnP-TTT as a new method for overcoming distribution shifts in PnP. PnP-TTT uses deep equilibrium learning (DEQ) for optimizing a self-supervised loss at the fixed points of PnP iterations. PnP-TTT can be directly applied on a single test sample to improve the generalization of PnP. We show through simulations that given a sufficient number of measurements, PnP-TTT enables the use of image priors trained on natural images for image reconstruction in magnetic resonance imaging (MRI).

PnP Restoration with Domain Adaptation for SANS

Small Angle Neutron Scattering (SANS) is a non-destructive technique utilized to probe the nano- to mesoscale structure of materials by analyzing the scattering pattern of neutrons. Accelerating SANS acquisition for in-situ analysis is essential, but it often reduces the signal-to-noise ratio (SNR), highlighting the need for methods to enhance SNR even with short acquisition times. While deep learning (DL) can be used for enhancing SNR of low quality SANS, the amount of experimental data available for training is usually severely limited. We address this issue by proposing a Plug-and-play Restoration for SANS (PR-SANS) that uses domain-adapted priors. The prior in PR-SANS is initially trained on a set of generic images and subsequently fine-tuned using a limited amount of experimental SANS data. We present a theoretical convergence analysis of PR-SANS by focusing on the error resulting from using inexact domain-adapted priors instead of the ideal ones. We demonstrate with experimentally collected SANS data that PR-SANS can recover high-SNR 2D SANS detector images from low-SNR detector images, effectively increasing the SNR. This advancement enables a reduction in acquisition times by a factor of 12 while maintaining the original signal quality.

Convergence of Nonconvex PnP-ADMM with MMSE Denoisers

Plug-and-Play Alternating Direction Method of Multipliers (PnP-ADMM) is a widely-used algorithm for solving inverse problems by integrating physical measurement models and convolutional neural network (CNN) priors. PnP-ADMM has been theoretically proven to converge for convex data-fidelity terms and nonexpansive CNNs. It has however been observed that PnP-ADMM often empirically converges even for expansive CNNs. This paper presents a theoretical explanation for the observed stability of PnP-ADMM based on the interpretation of the CNN prior as a minimum mean-squared error (MMSE) denoiser. Our explanation parallels a similar argument recently made for the iterative shrinkage/thresholding algorithm variant of PnP (PnP-ISTA) and relies on the connection between MMSE denoisers and proximal operators. We also numerically evaluate the performance gap between PnP-ADMM using a nonexpansive DnCNN denoiser and expansive DRUNet denoiser, thus motivating the use of expansive CNNs.

FLAIR: A Conditional Diffusion Framework with Applications to Face Video Restoration

Face video restoration (FVR) is a challenging but important problem where one seeks to recover a perceptually realistic face videos from a low-quality input. While diffusion probabilistic models (DPMs) have been shown to achieve remarkable performance for face image restoration, they often fail to preserve temporally coherent, high-quality videos, compromising the fidelity of reconstructed faces. We present a new conditional diffusion framework called FLAIR for FVR. FLAIR ensures temporal consistency across frames in a computationally efficient fashion by converting a traditional image DPM into a video DPM. The proposed conversion uses a recurrent video refinement layer and a temporal self-attention at different scales. FLAIR also uses a conditional iterative refinement process to balance the perceptual and distortion quality during inference. This process consists of two key components: a data-consistency module that analytically ensures that the generated video precisely matches its degraded observation and a coarse-to-fine image enhancement module specifically for facial regions. Our extensive experiments show superiority of FLAIR over the current state-of-the-art (SOTA) for video super-resolution, deblurring, JPEG restoration, and space-time frame interpolation on two high-quality face video datasets.

Prior Mismatch and Adaptation in PnP-ADMM with a Nonconvex Convergence Analysis

Plug-and-Play (PnP) priors is a widely-used family of methods for solving imaging inverse problems by integrating physical measurement models with image priors specified using image denoisers. PnP methods have been shown to achieve state-of-the-art performance when the prior is obtained using powerful deep denoisers. Despite extensive work on PnP, the topic of distribution mismatch between the training and testing data has often been overlooked in the PnP literature. This paper presents a set of new theoretical and numerical results on the topic of prior distribution mismatch and domain adaptation for alternating direction method of multipliers (ADMM) variant of PnP. Our theoretical result provides an explicit error bound for PnP-ADMM due to the mismatch between the desired denoiser and the one used for inference. Our analysis contributes to the work in the area by considering the mismatch under nonconvex data-fidelity terms and expansive denoisers. Our first set of numerical results quantifies the impact of the prior distribution mismatch on the performance of PnP-ADMM on the problem of image super-resolution. Our second set of numerical results considers a simple and effective domain adaption strategy that closes the performance gap due to the use of mismatched denoisers. Our results suggest the relative robustness of PnP-ADMM to prior distribution mismatch, while also showing that the performance gap can be significantly reduced with few training samples from the desired distribution.

Block Coordinate Plug-and-Play Methods for Blind Inverse Problems

Plug-and-play (PnP) prior is a well-known class of methods for solving imaging inverse problems by computing fixed-points of operators combining physical measurement models and learned image denoisers. While PnP methods have been extensively used for image recovery with known measurement operators, there is little work on PnP for solving blind inverse problems. We address this gap by presenting a new block-coordinate PnP (BC-PnP) method that efficiently solves this joint estimation problem by introducing learned denoisers as priors on both the unknown image and the unknown measurement operator. We present a new convergence theory for BC-PnP compatible with blind inverse problems by considering nonconvex data-fidelity terms and expansive denoisers. Our theory analyzes the convergence of BC-PnP to a stationary point of an implicit function associated with an approximate minimum mean-squared error (MMSE) denoiser. We numerically validate our method on two blind inverse problems: automatic coil sensitivity estimation in magnetic resonance imaging (MRI) and blind image deblurring. Our results show that BC-PnP provides an efficient and principled framework for using denoisers as PnP priors for jointly estimating measurement operators and images.

DOLPH: Diffusion Models for Phase Retrieval

Phase retrieval refers to the problem of recovering an image from the magnitudes of its complex-valued linear measurements. Since the problem is ill-posed, the recovery requires prior knowledge on the unknown image. We present DOLPH as a new deep model-based architecture for phase retrieval that integrates an image prior specified using a diffusion model with a nonconvex data-fidelity term for phase retrieval. Diffusion models are a recent class of deep generative models that are relatively easy to train due to their implementation as image denoisers. DOLPH reconstructs high-quality solutions by alternating data-consistency updates with the sampling step of a diffusion model. Our numerical results show the robustness of DOLPH to noise and its ability to generate several candidate solutions given a set of measurements.

Robustness of Deep Equilibrium Architectures to Changes in the Measurement Model

Deep model-based architectures (DMBAs) are widely used in imaging inverse problems to integrate physical measurement models and learned image priors. Plug-and-play priors (PnP) and deep equilibrium models (DEQ) are two DMBA frameworks that have received significant attention. The key difference between the two is that the image prior in DEQ is trained by using a specific measurement model, while that in PnP is trained as a general image denoiser. This difference is behind a common assumption that PnP is more robust to changes in the measurement models compared to DEQ. This paper investigates the robustness of DEQ priors to changes in the measurement models. Our results on two imaging inverse problems suggest that DEQ priors trained under mismatched measurement models outperform image denoisers.