An Adaptive Multiparameter Penalty Selection Method for Multiconstraint and Multiblock ADMM

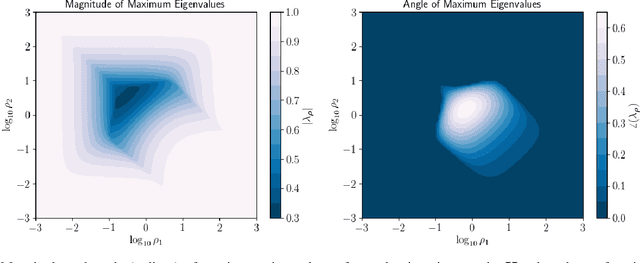
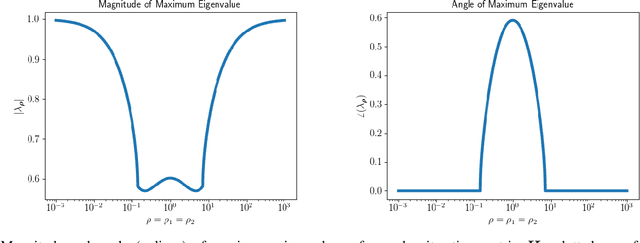
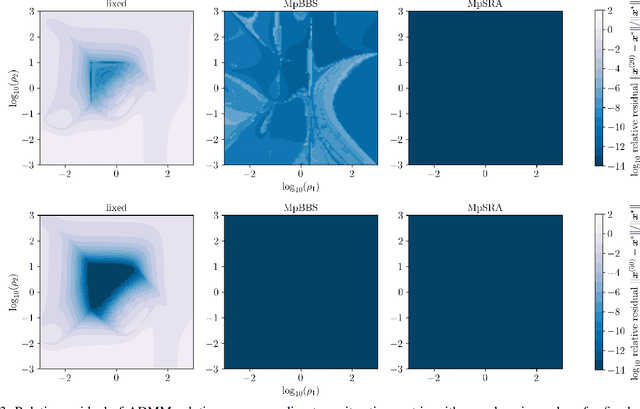
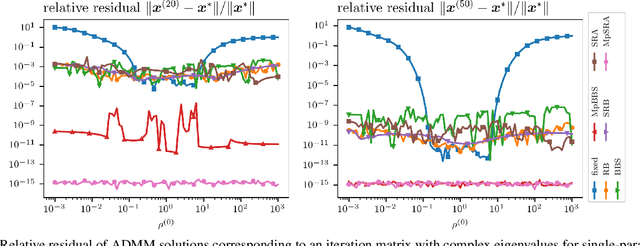
This work presents a new method for online selection of multiple penalty parameters for the alternating direction method of multipliers (ADMM) algorithm applied to optimization problems with multiple constraints or functionals with block matrix components. ADMM is widely used for solving constrained optimization problems in a variety of fields, including signal and image processing. Implementations of ADMM often utilize a single hyperparameter, referred to as the penalty parameter, which needs to be tuned to control the rate of convergence. However, in problems with multiple constraints, ADMM may demonstrate slow convergence regardless of penalty parameter selection due to scale differences between constraints. Accounting for scale differences between constraints to improve convergence in these cases requires introducing a penalty parameter for each constraint. The proposed method is able to adaptively account for differences in scale between constraints, providing robustness with respect to problem transformations and initial selection of penalty parameters. It is also simple to understand and implement. Our numerical experiments demonstrate that the proposed method performs favorably compared to a variety of existing penalty parameter selection methods.

Learned Correction Methods for Ultrasound Computed Tomography Imaging Using Simplified Physics Models

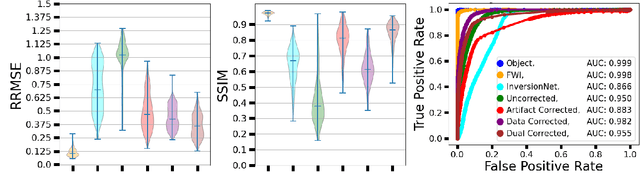
Ultrasound computed tomography (USCT) is an emerging modality for breast imaging. Image reconstruction methods that incorporate accurate wave physics produce high resolution quantitative images of acoustic properties but are computationally expensive. The use of a simplified linear model in reconstruction reduces computational expense at the cost of reduced accuracy. This work aims to systematically compare different learning approaches for USCT reconstruction utilizing simplified linear models. This work considered various learning approaches to compensate for errors stemming from a linearized wave propagation model: correction in the data and image domains. The resulting image reconstruction methods are systematically assessed, alongside data-driven and model-based methods, in four virtual imaging studies utilizing anatomically realistic numerical phantoms. Image quality was assessed utilizing relative root mean square error (RRMSE), structural similarity index measure (SSIM), and a task-based assessment for tumor detection. Correction in the measurement domain resulted in images with minor visual artifacts and highly accurate task performance. Correction in the image domain demonstrated a heavy bias on training data, resulting in hallucinations, but greater robustness to measurement noise. Combining both forms of correction performed best in terms of RRMSE and SSIM, at the cost of task performance. This work systematically assessed learned reconstruction methods incorporating an approximated physical model for USCT imaging. Results demonstrated the importance of incorporating physics, compared to data-driven methods. Learning a correction in the data domain led to better task performance and robust out-of-distribution generalization compared to correction in the image domain.

ProxNF: Neural Field Proximal Training for High-Resolution 4D Dynamic Image Reconstruction

Accurate spatiotemporal image reconstruction methods are needed for a wide range of biomedical research areas but face challenges due to data incompleteness and computational burden. Data incompleteness arises from the undersampling often required to increase frame rates and reduce acquisition times, while computational burden emerges due to the memory footprint of high-resolution images with three spatial dimensions and extended time horizons. Neural fields, an emerging class of neural networks that act as continuous representations of spatiotemporal objects, have previously been introduced to solve these dynamic imaging problems by reframing image reconstruction to a problem of estimating network parameters. Neural fields can address the twin challenges of data incompleteness and computational burden by exploiting underlying redundancies in these spatiotemporal objects. This work proposes ProxNF, a novel neural field training approach for spatiotemporal image reconstruction leveraging proximal splitting methods to separate computations involving the imaging operator from updates of the network parameter. Specifically, ProxNF evaluates the (subsampled) gradient of the data-fidelity term in the image domain and uses a fully supervised learning approach to update the neural field parameters. By reducing the memory footprint and the computational cost of evaluating the imaging operator, the proposed ProxNF approach allows for reconstructing large, high-resolution spatiotemporal images. This method is demonstrated in two numerical studies involving virtual dynamic contrast-enhanced photoacoustic computed tomography imaging of an anatomically realistic dynamic numerical mouse phantom and a two-compartment model of tumor perfusion.

Technical Note: An Efficient Implementation of the Spherical Radon Transform with Cylindrical Apertures

The spherical Radon transform (SRT) is an integral transform that maps a function to its integrals over concentric spherical shells centered at specified sensor locations. It has several imaging applications, including synthetic aperture radar and photoacoustic computed tomography. However, computation of the SRT can be expensive. Efficient implementation of SRT on general purpose graphic processing units (GPGPUs) often utilizes non-matched implementation of the adjoint operator, leading to inconsistent gradients in optimization-based image reconstruction methods. This work details an efficient implementation of the SRT and its adjoint for the case of a cylindrical measurement aperture. Exploiting symmetry of the cylindrical geometry, the SRT can then be expressed as the composition of two circular Radon transforms (CRT). Utilizing this formulation then allows for an efficient implementation of the SRT as a discrete-to-discrete operator utilizing sparse matrix representation.

Learned Full Waveform Inversion Incorporating Task Information for Ultrasound Computed Tomography

Ultrasound computed tomography (USCT) is an emerging imaging modality that holds great promise for breast imaging. Full-waveform inversion (FWI)-based image reconstruction methods incorporate accurate wave physics to produce high spatial resolution quantitative images of speed of sound or other acoustic properties of the breast tissues from USCT measurement data. However, the high computational cost of FWI reconstruction represents a significant burden for its widespread application in a clinical setting. The research reported here investigates the use of a convolutional neural network (CNN) to learn a mapping from USCT waveform data to speed of sound estimates. The CNN was trained using a supervised approach with a task-informed loss function aiming at preserving features of the image that are relevant to the detection of lesions. A large set of anatomically and physiologically realistic numerical breast phantoms (NBPs) and corresponding simulated USCT measurements was employed during training. Once trained, the CNN can perform real-time FWI image reconstruction from USCT waveform data. The performance of the proposed method was assessed and compared against FWI using a hold-out sample of 41 NBPs and corresponding USCT data. Accuracy was measured using relative mean square error (RMSE), structural self-similarity index measure (SSIM), and lesion detection performance (DICE score). This numerical experiment demonstrates that a supervised learning model can achieve accuracy comparable to FWI in terms of RMSE and SSIM, and better performance in terms of task performance, while significantly reducing computational time.

A Memory-Efficient Dynamic Image Reconstruction Method using Neural Fields

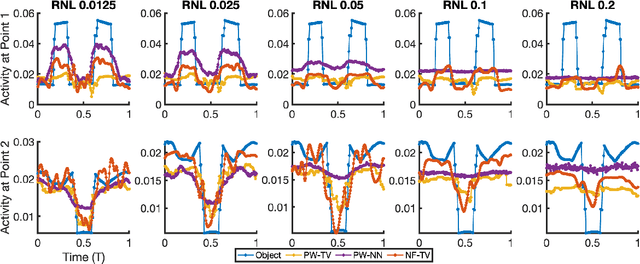
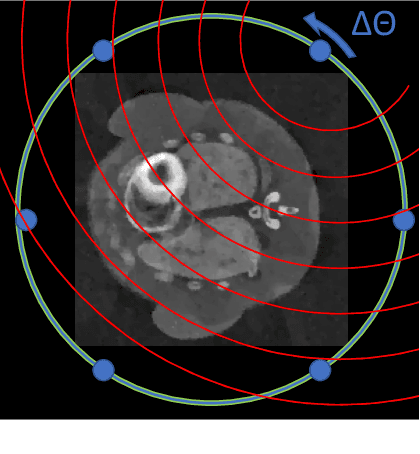
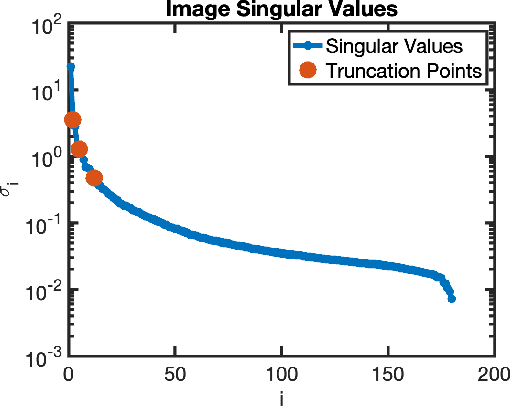
Dynamic imaging is essential for analyzing various biological systems and behaviors but faces two main challenges: data incompleteness and computational burden. For many imaging systems, high frame rates and short acquisition times require severe undersampling, which leads to data incompleteness. Multiple images may then be compatible with the data, thus requiring special techniques (regularization) to ensure the uniqueness of the reconstruction. Computational and memory requirements are particularly burdensome for three-dimensional dynamic imaging applications requiring high resolution in both space and time. Exploiting redundancies in the object's spatiotemporal features is key to addressing both challenges. This contribution investigates neural fields, or implicit neural representations, to model the sought-after dynamic object. Neural fields are a particular class of neural networks that represent the dynamic object as a continuous function of space and time, thus avoiding the burden of storing a full resolution image at each time frame. Neural field representation thus reduces the image reconstruction problem to estimating the network parameters via a nonlinear optimization problem (training). Once trained, the neural field can be evaluated at arbitrary locations in space and time, allowing for high-resolution rendering of the object. Key advantages of the proposed approach are that neural fields automatically learn and exploit redundancies in the sought-after object to both regularize the reconstruction and significantly reduce memory storage requirements. The feasibility of the proposed framework is illustrated with an application to dynamic image reconstruction from severely undersampled circular Radon transform data.