Inverse problem regularization with hierarchical variational autoencoders

In this paper, we propose to regularize ill-posed inverse problems using a deep hierarchical variational autoencoder (HVAE) as an image prior. The proposed method synthesizes the advantages of i) denoiser-based Plug \& Play approaches and ii) generative model based approaches to inverse problems. First, we exploit VAE properties to design an efficient algorithm that benefits from convergence guarantees of Plug-and-Play (PnP) methods. Second, our approach is not restricted to specialized datasets and the proposed PnP-HVAE model is able to solve image restoration problems on natural images of any size. Our experiments show that the proposed PnP-HVAE method is competitive with both SOTA denoiser-based PnP approaches, and other SOTA restoration methods based on generative models.

Diverse super-resolution with pretrained deep hiererarchical VAEs

Image super-resolution is a one-to-many problem, but most deep-learning based methods only provide one single solution to this problem. In this work, we tackle the problem of diverse super-resolution by reusing VD-VAE, a state-of-the art variational autoencoder (VAE). We find that the hierarchical latent representation learned by VD-VAE naturally separates the image low-frequency information, encoded in the latent groups at the top of the hierarchy, from the image high-frequency details, determined by the latent groups at the bottom of the latent hierarchy. Starting from this observation, we design a super-resolution model exploiting the specific structure of VD-VAE latent space. Specifically, we train an encoder to encode low-resolution images in the subset of VD-VAE latent space encoding the low-frequency information, and we combine this encoder with VD-VAE generative model to sample diverse super-resolved version of a low-resolution input. We demonstrate the ability of our method to generate diverse solutions to the super-resolution problem on face super-resolution with upsampling factors x4, x8, and x16.

Wasserstein Patch Prior for Image Superresolution

In this paper, we introduce a Wasserstein patch prior for superresolution of two- and three-dimensional images. Here, we assume that we have given (additionally to the low resolution observation) a reference image which has a similar patch distribution as the ground truth of the reconstruction. This assumption is e.g. fulfilled when working with texture images or material data. Then, the proposed regularizer penalizes the $W_2$-distance of the patch distribution of the reconstruction to the patch distribution of some reference image at different scales. We demonstrate the performance of the proposed regularizer by two- and three-dimensional numerical examples.

Learning local regularization for variational image restoration

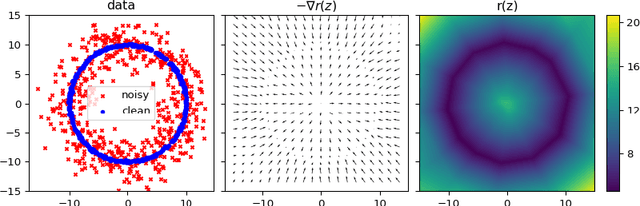
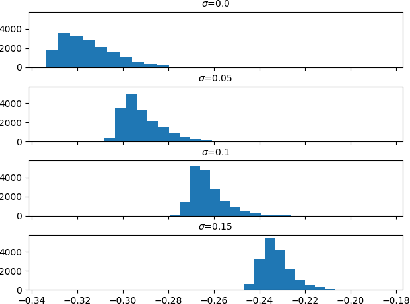
In this work, we propose a framework to learn a local regularization model for solving general image restoration problems. This regularizer is defined with a fully convolutional neural network that sees the image through a receptive field corresponding to small image patches. The regularizer is then learned as a critic between unpaired distributions of clean and degraded patches using a Wasserstein generative adversarial networks based energy. This yields a regularization function that can be incorporated in any image restoration problem. The efficiency of the framework is finally shown on denoising and deblurring applications.

On the Existence of Optimal Transport Gradient for Learning Generative Models

The use of optimal transport cost for learning generative models has become popular with Wasserstein Generative Adversarial Networks (WGAN). Training of WGAN relies on a theoretical background: the calculation of the gradient of the optimal transport cost with respect to the generative model parameters. We first demonstrate that such gradient may not be defined, which can result in numerical instabilities during gradient-based optimization. We address this issue by stating a valid differentiation theorem in the case of entropic regularized transport and specify conditions under which existence is ensured. By exploiting the discrete nature of empirical data, we formulate the gradient in a semi-discrete setting and propose an algorithm for the optimization of the generative model parameters. Finally, we illustrate numerically the advantage of the proposed framework.

Wasserstein Generative Models for Patch-based Texture Synthesis

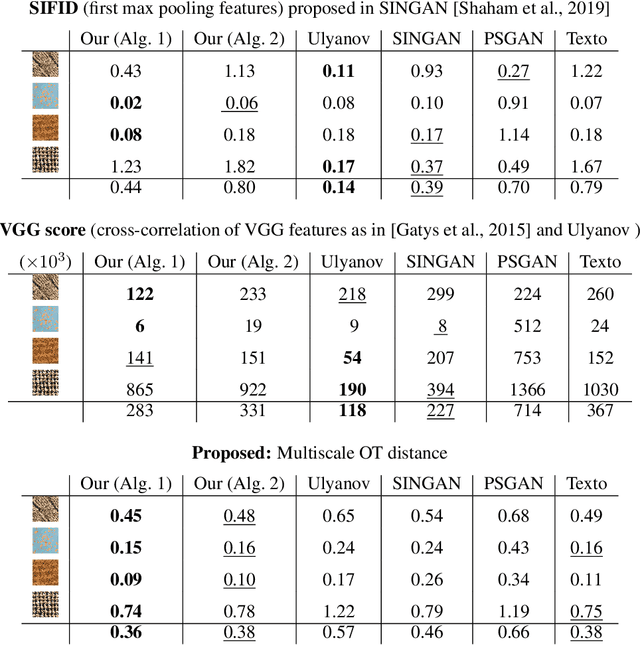
In this paper, we propose a framework to train a generative model for texture image synthesis from a single example. To do so, we exploit the local representation of images via the space of patches, that is, square sub-images of fixed size (e.g. $4\times 4$). Our main contribution is to consider optimal transport to enforce the multiscale patch distribution of generated images, which leads to two different formulations. First, a pixel-based optimization method is proposed, relying on discrete optimal transport. We show that it is related to a well-known texture optimization framework based on iterated patch nearest-neighbor projections, while avoiding some of its shortcomings. Second, in a semi-discrete setting, we exploit the differential properties of Wasserstein distances to learn a fully convolutional network for texture generation. Once estimated, this network produces realistic and arbitrarily large texture samples in real time. The two formulations result in non-convex concave problems that can be optimized efficiently with convergence properties and improved stability compared to adversarial approaches, without relying on any regularization. By directly dealing with the patch distribution of synthesized images, we also overcome limitations of state-of-the art techniques, such as patch aggregation issues that usually lead to low frequency artifacts (e.g. blurring) in traditional patch-based approaches, or statistical inconsistencies (e.g. color or patterns) in learning approaches.