Wasserstein Generative Models for Patch-based Texture Synthesis

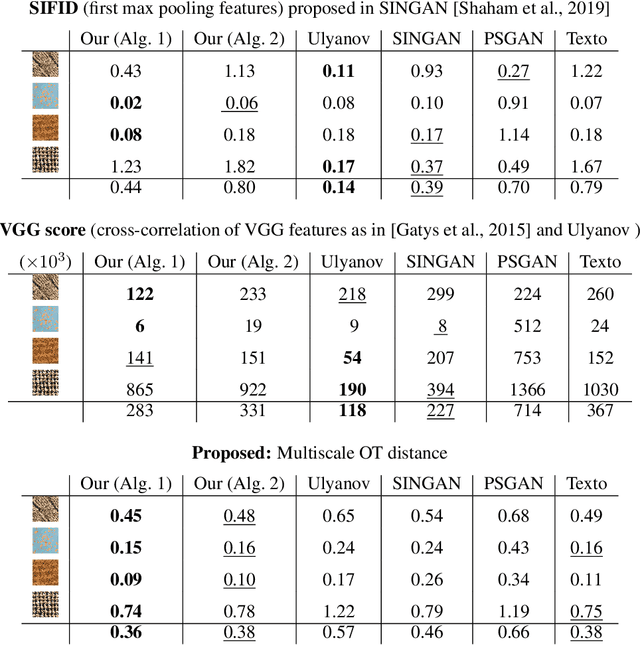
In this paper, we propose a framework to train a generative model for texture image synthesis from a single example. To do so, we exploit the local representation of images via the space of patches, that is, square sub-images of fixed size (e.g. $4\times 4$). Our main contribution is to consider optimal transport to enforce the multiscale patch distribution of generated images, which leads to two different formulations. First, a pixel-based optimization method is proposed, relying on discrete optimal transport. We show that it is related to a well-known texture optimization framework based on iterated patch nearest-neighbor projections, while avoiding some of its shortcomings. Second, in a semi-discrete setting, we exploit the differential properties of Wasserstein distances to learn a fully convolutional network for texture generation. Once estimated, this network produces realistic and arbitrarily large texture samples in real time. The two formulations result in non-convex concave problems that can be optimized efficiently with convergence properties and improved stability compared to adversarial approaches, without relying on any regularization. By directly dealing with the patch distribution of synthesized images, we also overcome limitations of state-of-the art techniques, such as patch aggregation issues that usually lead to low frequency artifacts (e.g. blurring) in traditional patch-based approaches, or statistical inconsistencies (e.g. color or patterns) in learning approaches.