Random Forests for Big Data

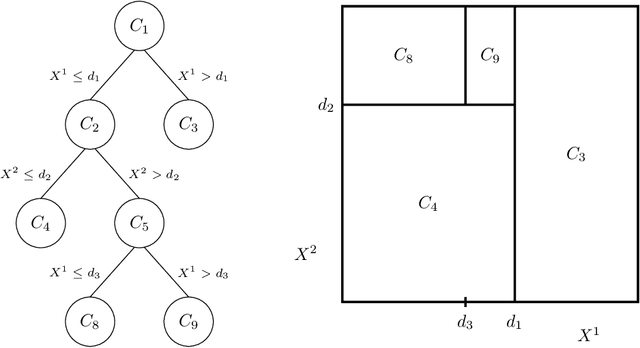
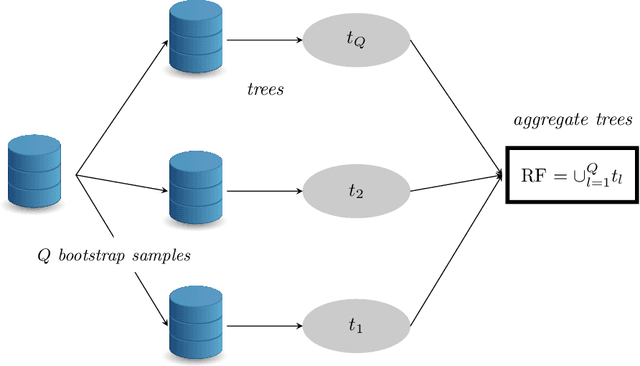
Big Data is one of the major challenges of statistical science and has numerous consequences from algorithmic and theoretical viewpoints. Big Data always involve massive data but they also often include online data and data heterogeneity. Recently some statistical methods have been adapted to process Big Data, like linear regression models, clustering methods and bootstrapping schemes. Based on decision trees combined with aggregation and bootstrap ideas, random forests were introduced by Breiman in 2001. They are a powerful nonparametric statistical method allowing to consider in a single and versatile framework regression problems, as well as two-class and multi-class classification problems. Focusing on classification problems, this paper proposes a selective review of available proposals that deal with scaling random forests to Big Data problems. These proposals rely on parallel environments or on online adaptations of random forests. We also describe how related quantities -- such as out-of-bag error and variable importance -- are addressed in these methods. Then, we formulate various remarks for random forests in the Big Data context. Finally, we experiment five variants on two massive datasets (15 and 120 millions of observations), a simulated one as well as real world data. One variant relies on subsampling while three others are related to parallel implementations of random forests and involve either various adaptations of bootstrap to Big Data or to "divide-and-conquer" approaches. The fifth variant relates on online learning of random forests. These numerical experiments lead to highlight the relative performance of the different variants, as well as some of their limitations.

Statistique et Big Data Analytics; Volumétrie, L'Attaque des Clones

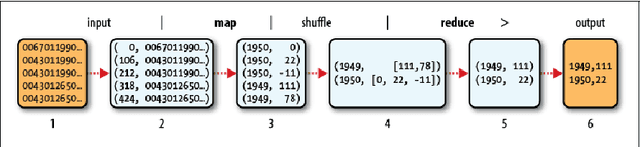
This article assumes acquired the skills and expertise of a statistician in unsupervised (NMF, k-means, SVD) and supervised learning (regression, CART, random forest). What skills and knowledge do a statistician must acquire to reach the "Volume" scale of big data? After a quick overview of the different strategies available and especially of those imposed by Hadoop, the algorithms of some available learning methods are outlined in order to understand how they are adapted to the strong stresses of the Map-Reduce functionalities

On-line relational SOM for dissimilarity data

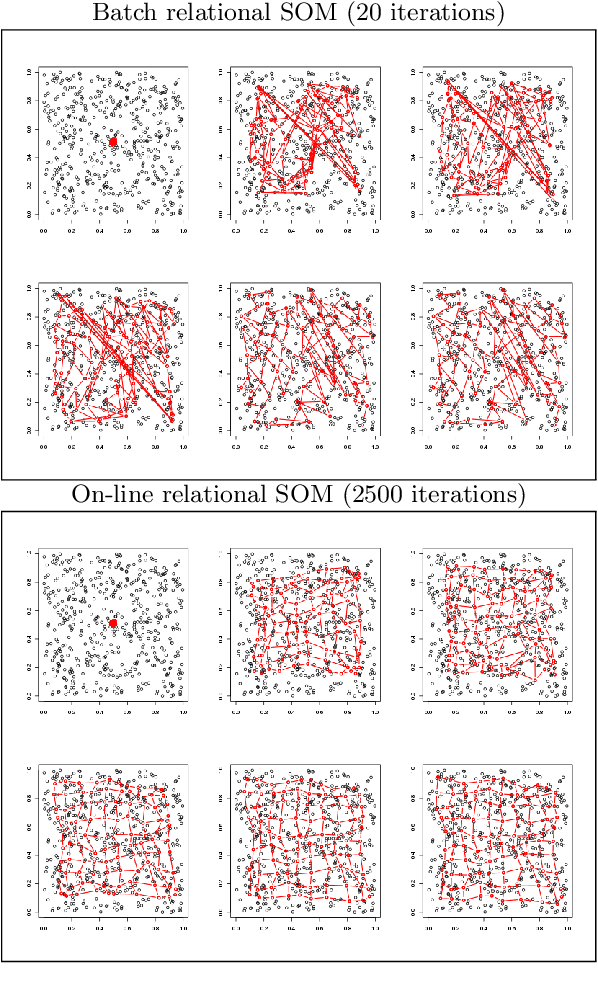
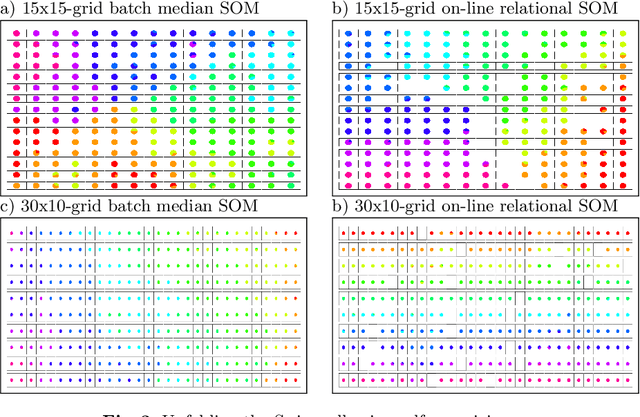
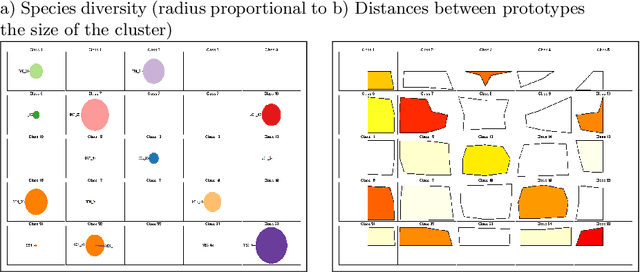
In some applications and in order to address real world situations better, data may be more complex than simple vectors. In some examples, they can be known through their pairwise dissimilarities only. Several variants of the Self Organizing Map algorithm were introduced to generalize the original algorithm to this framework. Whereas median SOM is based on a rough representation of the prototypes, relational SOM allows representing these prototypes by a virtual combination of all elements in the data set. However, this latter approach suffers from two main drawbacks. First, its complexity can be large. Second, only a batch version of this algorithm has been studied so far and it often provides results having a bad topographic organization. In this article, an on-line version of relational SOM is described and justified. The algorithm is tested on several datasets, including categorical data and graphs, and compared with the batch version and with other SOM algorithms for non vector data.

Neural Networks for Complex Data

Artificial neural networks are simple and efficient machine learning tools. Defined originally in the traditional setting of simple vector data, neural network models have evolved to address more and more difficulties of complex real world problems, ranging from time evolving data to sophisticated data structures such as graphs and functions. This paper summarizes advances on those themes from the last decade, with a focus on results obtained by members of the SAMM team of Universit\'e Paris 1

Optimizing an Organized Modularity Measure for Topographic Graph Clustering: a Deterministic Annealing Approach

This paper proposes an organized generalization of Newman and Girvan's modularity measure for graph clustering. Optimized via a deterministic annealing scheme, this measure produces topologically ordered graph clusterings that lead to faithful and readable graph representations based on clustering induced graphs. Topographic graph clustering provides an alternative to more classical solutions in which a standard graph clustering method is applied to build a simpler graph that is then represented with a graph layout algorithm. A comparative study on four real world graphs ranging from 34 to 1 133 vertices shows the interest of the proposed approach with respect to classical solutions and to self-organizing maps for graphs.