Cross-validation
Paper and Code
Mar 09, 2017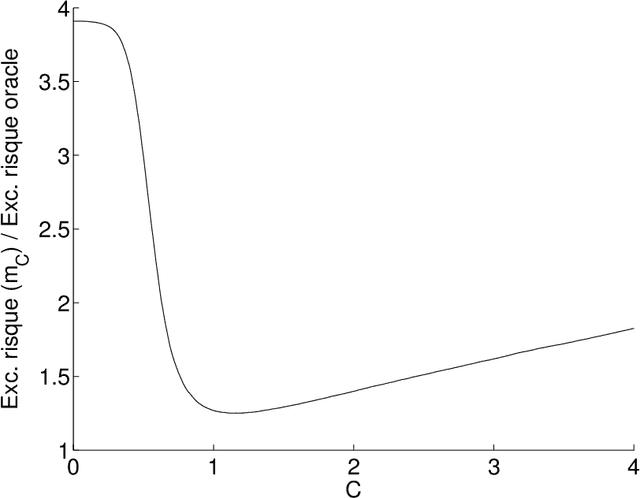
This text is a survey on cross-validation. We define all classical cross-validation procedures, and we study their properties for two different goals: estimating the risk of a given estimator, and selecting the best estimator among a given family. For the risk estimation problem, we compute the bias (which can also be corrected) and the variance of cross-validation methods. For estimator selection, we first provide a first-order analysis (based on expectations). Then, we explain how to take into account second-order terms (from variance computations, and by taking into account the usefulness of overpenalization). This allows, in the end, to provide some guidelines for choosing the best cross-validation method for a given learning problem.
* in French
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge