Choice of V for V-Fold Cross-Validation in Least-Squares Density Estimation
Paper and Code
Oct 11, 2015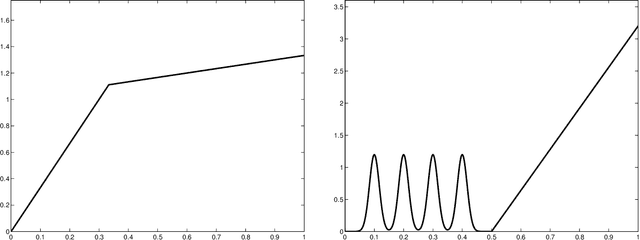

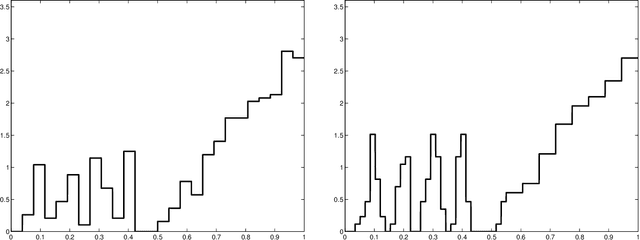
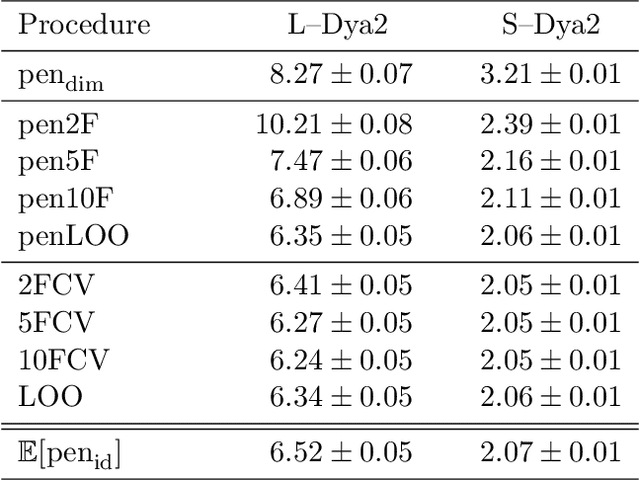
This paper studies V-fold cross-validation for model selection in least-squares density estimation. The goal is to provide theoretical grounds for choosing V in order to minimize the least-squares loss of the selected estimator. We first prove a non-asymptotic oracle inequality for V-fold cross-validation and its bias-corrected version (V-fold penalization). In particular, this result implies that V-fold penalization is asymptotically optimal in the nonparametric case. Then, we compute the variance of V-fold cross-validation and related criteria, as well as the variance of key quantities for model selection performance. We show that these variances depend on V like 1+4/(V-1), at least in some particular cases, suggesting that the performance increases much from V=2 to V=5 or 10, and then is almost constant. Overall, this can explain the common advice to take V=5---at least in our setting and when the computational power is limited---, as supported by some simulation experiments. An oracle inequality and exact formulas for the variance are also proved for Monte-Carlo cross-validation, also known as repeated cross-validation, where the parameter V is replaced by the number B of random splits of the data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge