Detecting multiple change-points in the time-varying Ising model

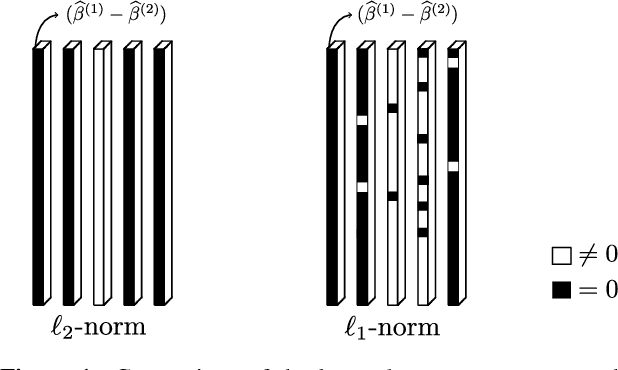
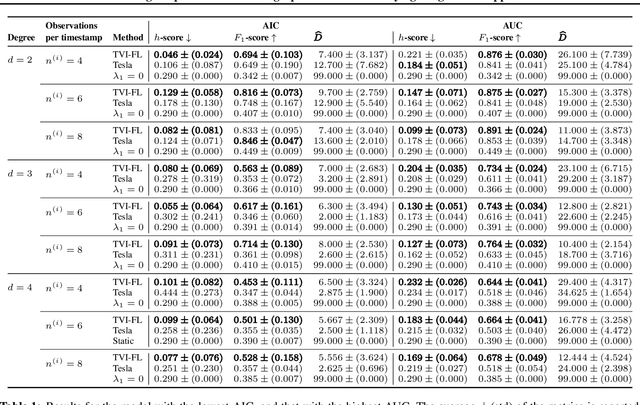
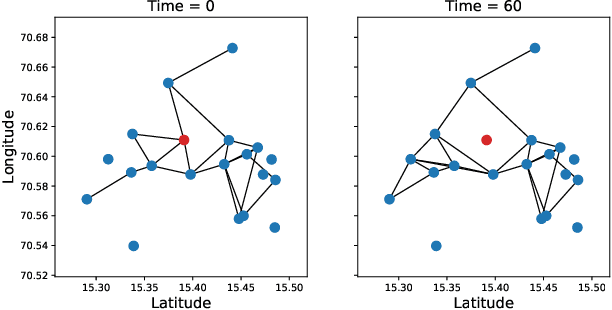
This work focuses on the estimation of change-points in a time-varying Ising graphical model (outputs $-1$ or $1$) evolving in a piecewise constant fashion. The occurring changes alter the graphical structure of the model, a structure which we also estimate in the present paper. For this purpose, we propose a new optimization program consisting in the minimization of a penalized negative conditional log-likelihood. The objective of the penalization is twofold: it imposes the learned graphs to be sparse and, thanks to a fused-type penalty, it enforces them to evolve piecewise constantly. Using few assumptions, we then give a change-point consistency theorem. Up to our knowledge, we are the first to present such theoretical result in the context of time-varying Ising model. Finally, experimental results on several synthetic examples and a real-world dataset demonstrate the empirical performance of our method.