Achieving Exact Cluster Recovery Threshold via Semidefinite Programming
Paper and Code
Jan 05, 2016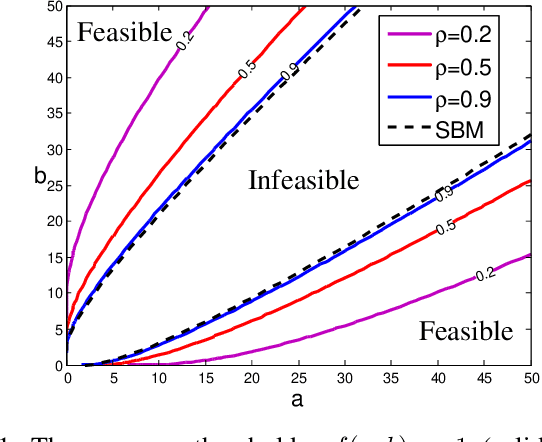
The binary symmetric stochastic block model deals with a random graph of $n$ vertices partitioned into two equal-sized clusters, such that each pair of vertices is connected independently with probability $p$ within clusters and $q$ across clusters. In the asymptotic regime of $p=a \log n/n$ and $q=b \log n/n$ for fixed $a,b$ and $n \to \infty$, we show that the semidefinite programming relaxation of the maximum likelihood estimator achieves the optimal threshold for exactly recovering the partition from the graph with probability tending to one, resolving a conjecture of Abbe et al. \cite{Abbe14}. Furthermore, we show that the semidefinite programming relaxation also achieves the optimal recovery threshold in the planted dense subgraph model containing a single cluster of size proportional to $n$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge