Regenerative Particle Thompson Sampling
Paper and Code
Mar 15, 2022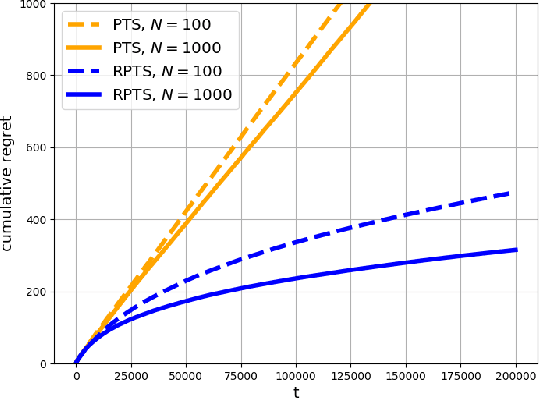
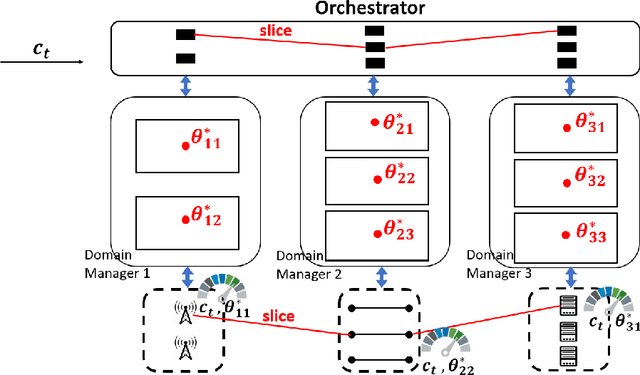
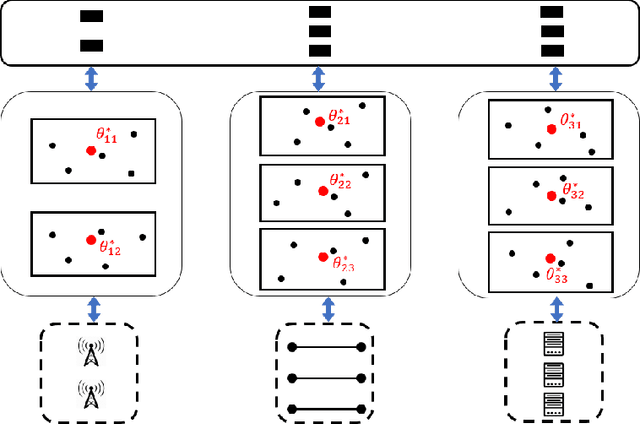
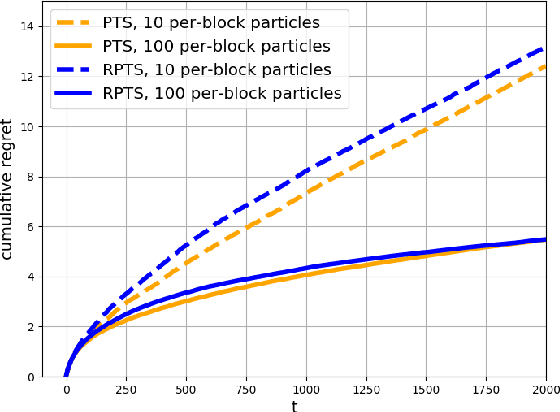
This paper proposes regenerative particle Thompson sampling (RPTS), a flexible variation of Thompson sampling. Thompson sampling itself is a Bayesian heuristic for solving stochastic bandit problems, but it is hard to implement in practice due to the intractability of maintaining a continuous posterior distribution. Particle Thompson sampling (PTS) is an approximation of Thompson sampling obtained by simply replacing the continuous distribution by a discrete distribution supported at a set of weighted static particles. We observe that in PTS, the weights of all but a few fit particles converge to zero. RPTS is based on the heuristic: delete the decaying unfit particles and regenerate new particles in the vicinity of fit surviving particles. Empirical evidence shows uniform improvement from PTS to RPTS and flexibility and efficacy of RPTS across a set of representative bandit problems, including an application to 5G network slicing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge