QWO: Speeding Up Permutation-Based Causal Discovery in LiGAMs

Causal discovery is essential for understanding relationships among variables of interest in many scientific domains. In this paper, we focus on permutation-based methods for learning causal graphs in Linear Gaussian Acyclic Models (LiGAMs), where the permutation encodes a causal ordering of the variables. Existing methods in this setting are not scalable due to their high computational complexity. These methods are comprised of two main components: (i) constructing a specific DAG, $\mathcal{G}^\pi$, for a given permutation $\pi$, which represents the best structure that can be learned from the available data while adhering to $\pi$, and (ii) searching over the space of permutations (i.e., causal orders) to minimize the number of edges in $\mathcal{G}^\pi$. We introduce QWO, a novel approach that significantly enhances the efficiency of computing $\mathcal{G}^\pi$ for a given permutation $\pi$. QWO has a speed-up of $O(n^2)$ ($n$ is the number of variables) compared to the state-of-the-art BIC-based method, making it highly scalable. We show that our method is theoretically sound and can be integrated into existing search strategies such as GRASP and hill-climbing-based methods to improve their performance.

Causal Effect Identification in a Sub-Population with Latent Variables

The s-ID problem seeks to compute a causal effect in a specific sub-population from the observational data pertaining to the same sub population (Abouei et al., 2023). This problem has been addressed when all the variables in the system are observable. In this paper, we consider an extension of the s-ID problem that allows for the presence of latent variables. To tackle the challenges induced by the presence of latent variables in a sub-population, we first extend the classical relevant graphical definitions, such as c-components and Hedges, initially defined for the so-called ID problem (Pearl, 1995; Tian & Pearl, 2002), to their new counterparts. Subsequently, we propose a sound algorithm for the s-ID problem with latent variables.

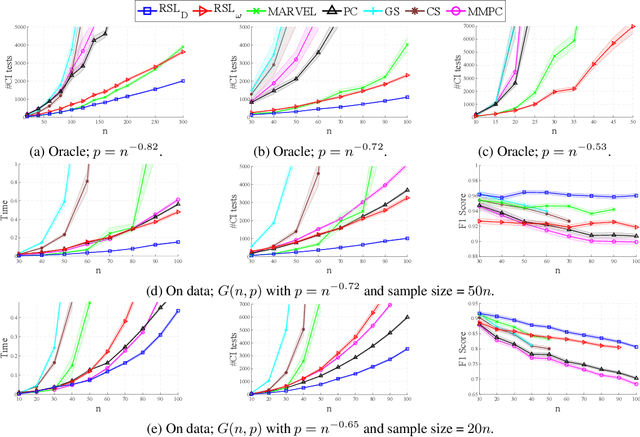
Recursive Causal Discovery

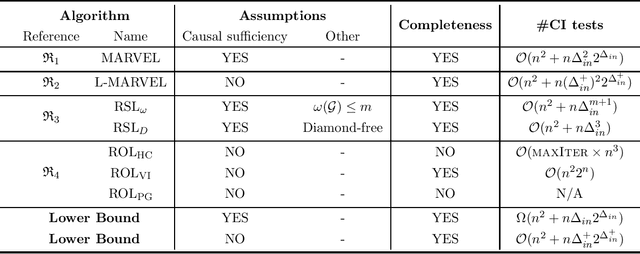
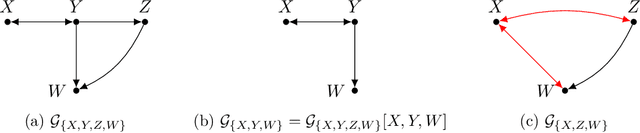
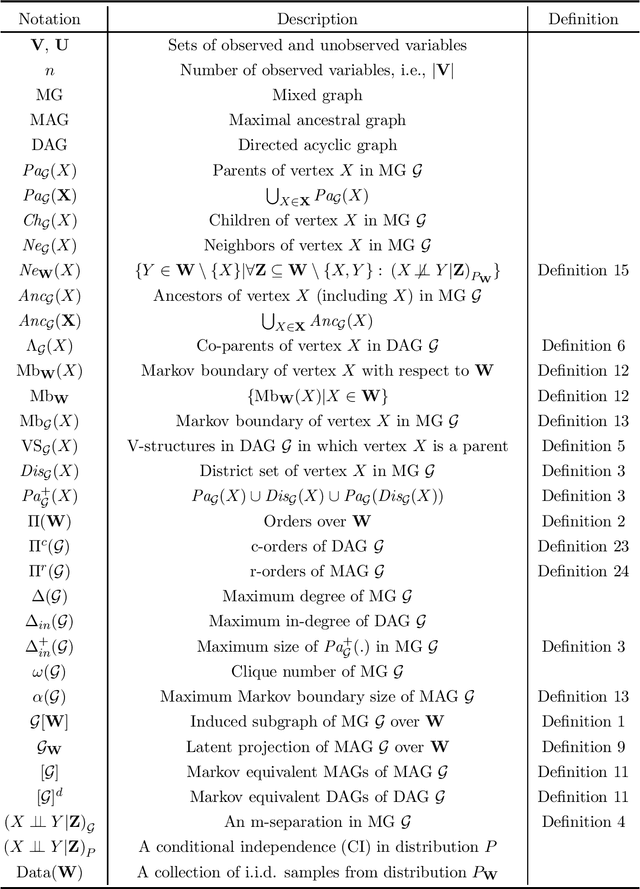
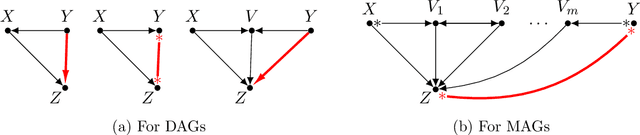
Causal discovery, i.e., learning the causal graph from data, is often the first step toward the identification and estimation of causal effects, a key requirement in numerous scientific domains. Causal discovery is hampered by two main challenges: limited data results in errors in statistical testing and the computational complexity of the learning task is daunting. This paper builds upon and extends four of our prior publications (Mokhtarian et al., 2021; Akbari et al., 2021; Mokhtarian et al., 2022, 2023a). These works introduced the concept of removable variables, which are the only variables that can be removed recursively for the purpose of causal discovery. Presence and identification of removable variables allow recursive approaches for causal discovery, a promising solution that helps to address the aforementioned challenges by reducing the problem size successively. This reduction not only minimizes conditioning sets in each conditional independence (CI) test, leading to fewer errors but also significantly decreases the number of required CI tests. The worst-case performances of these methods nearly match the lower bound. In this paper, we present a unified framework for the proposed algorithms, refined with additional details and enhancements for a coherent presentation. A comprehensive literature review is also included, comparing the computational complexity of our methods with existing approaches, showcasing their state-of-the-art efficiency. Another contribution of this paper is the release of RCD, a Python package that efficiently implements these algorithms. This package is designed for practitioners and researchers interested in applying these methods in practical scenarios. The package is available at github.com/ban-epfl/rcd, with comprehensive documentation provided at rcdpackage.com.

CausalCite: A Causal Formulation of Paper Citations

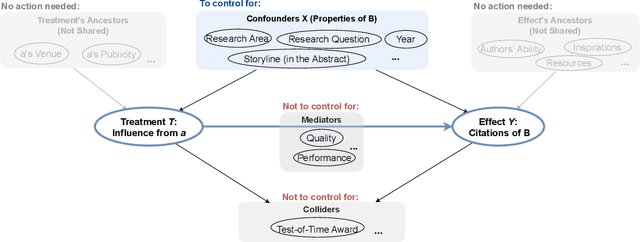
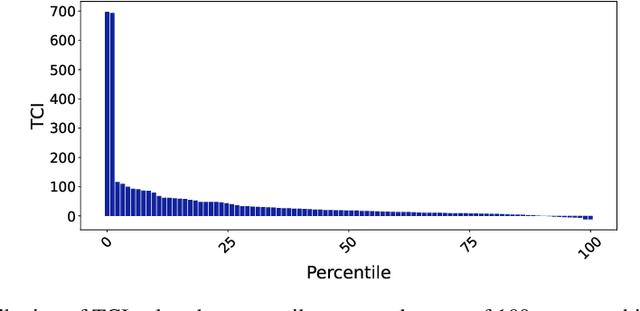
Evaluating the significance of a paper is pivotal yet challenging for the scientific community. While the citation count is the most commonly used proxy for this purpose, they are widely criticized for failing to accurately reflect a paper's true impact. In this work, we propose a causal inference method, TextMatch, which adapts the traditional matching framework to high-dimensional text embeddings. Specifically, we encode each paper using the text embeddings by large language models (LLMs), extract similar samples by cosine similarity, and synthesize a counterfactual sample by the weighted average of similar papers according to their similarity values. We apply the resulting metric, called CausalCite, as a causal formulation of paper citations. We show its effectiveness on various criteria, such as high correlation with paper impact as reported by scientific experts on a previous dataset of 1K papers, (test-of-time) awards for past papers, and its stability across various sub-fields of AI. We also provide a set of findings that can serve as suggested ways for future researchers to use our metric for a better understanding of a paper's quality. Our code and data are at https://github.com/causalNLP/causal-cite.

s-ID: Causal Effect Identification in a Sub-Population

Causal inference in a sub-population involves identifying the causal effect of an intervention on a specific subgroup within a larger population. However, ignoring the subtleties introduced by sub-populations can either lead to erroneous inference or limit the applicability of existing methods. We introduce and advocate for a causal inference problem in sub-populations (henceforth called s-ID), in which we merely have access to observational data of the targeted sub-population (as opposed to the entire population). Existing inference problems in sub-populations operate on the premise that the given data distributions originate from the entire population, thus, cannot tackle the s-ID problem. To address this gap, we provide necessary and sufficient conditions that must hold in the causal graph for a causal effect in a sub-population to be identifiable from the observational distribution of that sub-population. Given these conditions, we present a sound and complete algorithm for the s-ID problem.

Novel Ordering-based Approaches for Causal Structure Learning in the Presence of Unobserved Variables

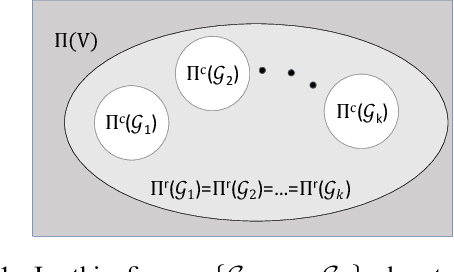
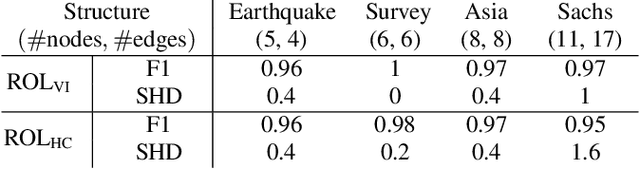
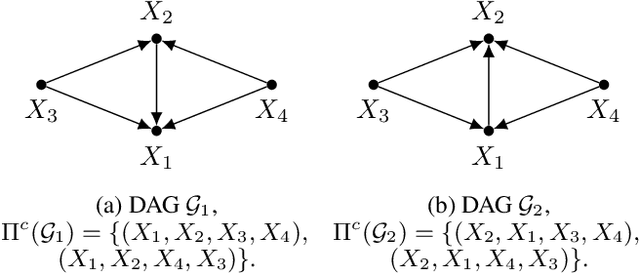
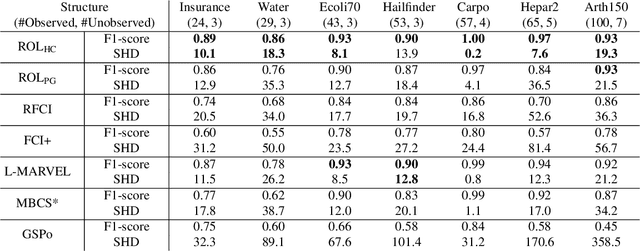
We propose ordering-based approaches for learning the maximal ancestral graph (MAG) of a structural equation model (SEM) up to its Markov equivalence class (MEC) in the presence of unobserved variables. Existing ordering-based methods in the literature recover a graph through learning a causal order (c-order). We advocate for a novel order called removable order (r-order) as they are advantageous over c-orders for structure learning. This is because r-orders are the minimizers of an appropriately defined optimization problem that could be either solved exactly (using a reinforcement learning approach) or approximately (using a hill-climbing search). Moreover, the r-orders (unlike c-orders) are invariant among all the graphs in a MEC and include c-orders as a subset. Given that set of r-orders is often significantly larger than the set of c-orders, it is easier for the optimization problem to find an r-order instead of a c-order. We evaluate the performance and the scalability of our proposed approaches on both real-world and randomly generated networks.

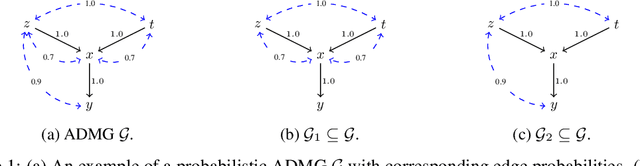
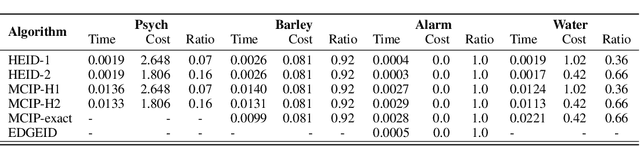
Causal Discovery in Probabilistic Networks with an Identifiable Causal Effect

Causal identification is at the core of the causal inference literature, where complete algorithms have been proposed to identify causal queries of interest. The validity of these algorithms hinges on the restrictive assumption of having access to a correctly specified causal structure. In this work, we study the setting where a probabilistic model of the causal structure is available. Specifically, the edges in a causal graph are assigned probabilities which may, for example, represent degree of belief from domain experts. Alternatively, the uncertainly about an edge may reflect the confidence of a particular statistical test. The question that naturally arises in this setting is: Given such a probabilistic graph and a specific causal effect of interest, what is the subgraph which has the highest plausibility and for which the causal effect is identifiable? We show that answering this question reduces to solving an NP-hard combinatorial optimization problem which we call the edge ID problem. We propose efficient algorithms to approximate this problem, and evaluate our proposed algorithms against real-world networks and randomly generated graphs.

Revisiting the General Identifiability Problem

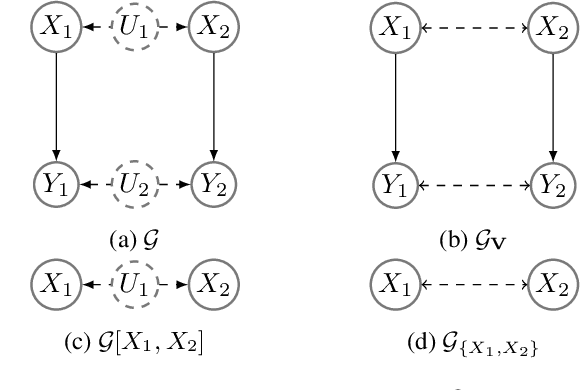
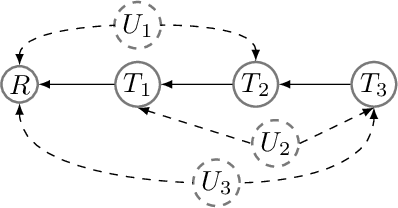
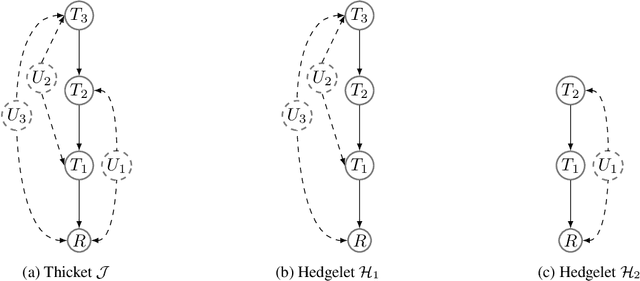
We revisit the problem of general identifiability originally introduced in [Lee et al., 2019] for causal inference and note that it is necessary to add positivity assumption of observational distribution to the original definition of the problem. We show that without such an assumption the rules of do-calculus and consequently the proposed algorithm in [Lee et al., 2019] are not sound. Moreover, adding the assumption will cause the completeness proof in [Lee et al., 2019] to fail. Under positivity assumption, we present a new algorithm that is provably both sound and complete. A nice property of this new algorithm is that it establishes a connection between general identifiability and classical identifiability by Pearl [1995] through decomposing the general identifiability problem into a series of classical identifiability sub-problems.

A Unified Experiment Design Approach for Cyclic and Acyclic Causal Models

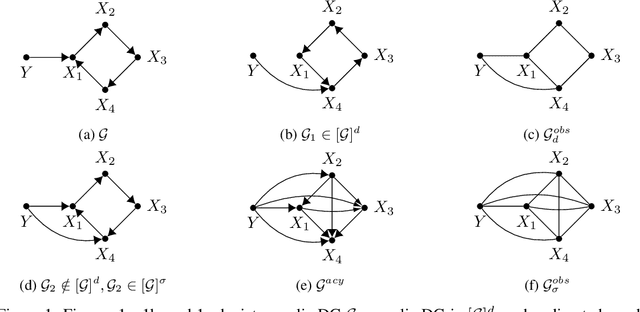
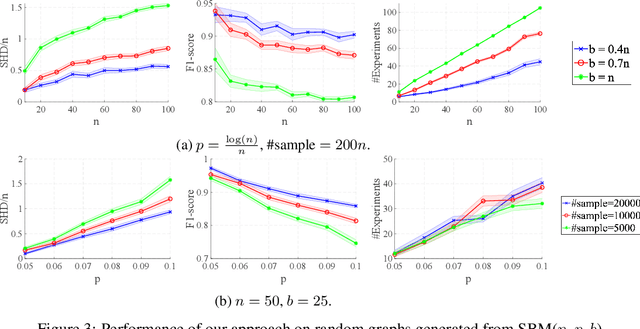
We study experiment design for the unique identification of the causal graph of a system where the graph may contain cycles. The presence of cycles in the structure introduces major challenges for experiment design. Unlike the case of acyclic graphs, learning the skeleton of the causal graph from observational distribution may not be possible. Furthermore, intervening on a variable does not necessarily lead to orienting all the edges incident to it. In this paper, we propose an experiment design approach that can learn both cyclic and acyclic graphs and hence, unifies the task of experiment design for both types of graphs. We provide a lower bound on the number of experiments required to guarantee the unique identification of the causal graph in the worst case, showing that the proposed approach is order-optimal in terms of the number of experiments up to an additive logarithmic term. Moreover, we extend our result to the setting where the size of each experiment is bounded by a constant. For this case, we show that our approach is optimal in terms of the size of the largest experiment required for the unique identification of the causal graph in the worst case.

Learning Bayesian Networks in the Presence of Structural Side Information

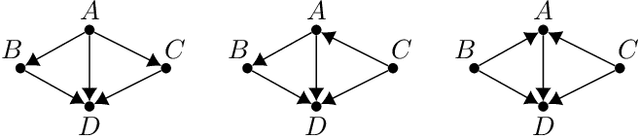
We study the problem of learning a Bayesian network (BN) of a set of variables when structural side information about the system is available. It is well known that learning the structure of a general BN is both computationally and statistically challenging. However, often in many applications, side information about the underlying structure can potentially reduce the learning complexity. In this paper, we develop a recursive constraint-based algorithm that efficiently incorporates such knowledge (i.e., side information) into the learning process. In particular, we study two types of structural side information about the underlying BN: (I) an upper bound on its clique number is known, or (II) it is diamond-free. We provide theoretical guarantees for the learning algorithms, including the worst-case number of tests required in each scenario. As a consequence of our work, we show that bounded treewidth BNs can be learned with polynomial complexity. Furthermore, we evaluate the performance and the scalability of our algorithms in both synthetic and real-world structures and show that they outperform the state-of-the-art structure learning algorithms.