Sample Complexity of Nonparametric Closeness Testing for Continuous Distributions and Its Application to Causal Discovery with Hidden Confounding

We study the problem of closeness testing for continuous distributions and its implications for causal discovery. Specifically, we analyze the sample complexity of distinguishing whether two multidimensional continuous distributions are identical or differ by at least $\epsilon$ in terms of Kullback-Leibler (KL) divergence under non-parametric assumptions. To this end, we propose an estimator of KL divergence which is based on the von Mises expansion. Our closeness test attains optimal parametric rates under smoothness assumptions. Equipped with this test, which serves as a building block of our causal discovery algorithm to identify the causal structure between two multidimensional random variables, we establish sample complexity guarantees for our causal discovery method. To the best of our knowledge, this work is the first work that provides sample complexity guarantees for distinguishing cause and effect in multidimensional non-linear models with non-Gaussian continuous variables in the presence of unobserved confounding.

Graph-Dependent Regret Bounds in Multi-Armed Bandits with Interference

Multi-armed bandits (MABs) are frequently used for online sequential decision-making in applications ranging from recommending personalized content to assigning treatments to patients. A recurring challenge in the applicability of the classic MAB framework to real-world settings is ignoring \textit{interference}, where a unit's outcome depends on treatment assigned to others. This leads to an exponentially growing action space, rendering standard approaches computationally impractical. We study the MAB problem under network interference, where each unit's reward depends on its own treatment and those of its neighbors in a given interference graph. We propose a novel algorithm that uses the local structure of the interference graph to minimize regret. We derive a graph-dependent upper bound on cumulative regret showing that it improves over prior work. Additionally, we provide the first lower bounds for bandits with arbitrary network interference, where each bound involves a distinct structural property of the interference graph. These bounds demonstrate that when the graph is either dense or sparse, our algorithm is nearly optimal, with upper and lower bounds that match up to logarithmic factors. We complement our theoretical results with numerical experiments, which show that our approach outperforms baseline methods.

Confounded Budgeted Causal Bandits

We study the problem of learning 'good' interventions in a stochastic environment modeled by its underlying causal graph. Good interventions refer to interventions that maximize rewards. Specifically, we consider the setting of a pre-specified budget constraint, where interventions can have non-uniform costs. We show that this problem can be formulated as maximizing the expected reward for a stochastic multi-armed bandit with side information. We propose an algorithm to minimize the cumulative regret in general causal graphs. This algorithm trades off observations and interventions based on their costs to achieve the optimal reward. This algorithm generalizes the state-of-the-art methods by allowing non-uniform costs and hidden confounders in the causal graph. Furthermore, we develop an algorithm to minimize the simple regret in the budgeted setting with non-uniform costs and also general causal graphs. We provide theoretical guarantees, including both upper and lower bounds, as well as empirical evaluations of our algorithms. Our empirical results showcase that our algorithms outperform the state of the art.

On sample complexity of conditional independence testing with Von Mises estimator with application to causal discovery

Motivated by conditional independence testing, an essential step in constraint-based causal discovery algorithms, we study the nonparametric Von Mises estimator for the entropy of multivariate distributions built on a kernel density estimator. We establish an exponential concentration inequality for this estimator. We design a test for conditional independence (CI) based on our estimator, called VM-CI, which achieves optimal parametric rates under smoothness assumptions. Leveraging the exponential concentration, we prove a tight upper bound for the overall error of VM-CI. This, in turn, allows us to characterize the sample complexity of any constraint-based causal discovery algorithm that uses VM-CI for CI tests. To the best of our knowledge, this is the first sample complexity guarantee for causal discovery for continuous variables. Furthermore, we empirically show that VM-CI outperforms other popular CI tests in terms of either time or sample complexity (or both), which translates to a better performance in structure learning as well.

Causal Imitability Under Context-Specific Independence Relations

Drawbacks of ignoring the causal mechanisms when performing imitation learning have recently been acknowledged. Several approaches both to assess the feasibility of imitation and to circumvent causal confounding and causal misspecifications have been proposed in the literature. However, the potential benefits of the incorporation of additional information about the underlying causal structure are left unexplored. An example of such overlooked information is context-specific independence (CSI), i.e., independence that holds only in certain contexts. We consider the problem of causal imitation learning when CSI relations are known. We prove that the decision problem pertaining to the feasibility of imitation in this setting is NP-hard. Further, we provide a necessary graphical criterion for imitation learning under CSI and show that under a structural assumption, this criterion is also sufficient. Finally, we propose a sound algorithmic approach for causal imitation learning which takes both CSI relations and data into account.

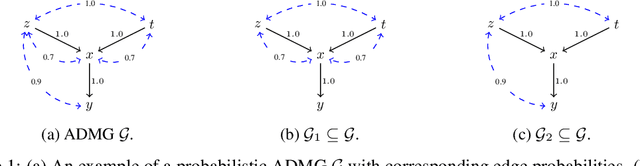
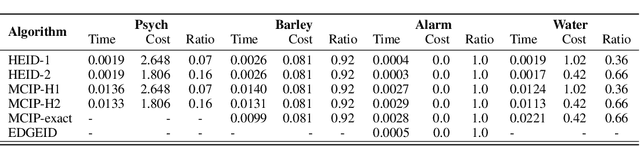
Causal Discovery in Probabilistic Networks with an Identifiable Causal Effect

Causal identification is at the core of the causal inference literature, where complete algorithms have been proposed to identify causal queries of interest. The validity of these algorithms hinges on the restrictive assumption of having access to a correctly specified causal structure. In this work, we study the setting where a probabilistic model of the causal structure is available. Specifically, the edges in a causal graph are assigned probabilities which may, for example, represent degree of belief from domain experts. Alternatively, the uncertainly about an edge may reflect the confidence of a particular statistical test. The question that naturally arises in this setting is: Given such a probabilistic graph and a specific causal effect of interest, what is the subgraph which has the highest plausibility and for which the causal effect is identifiable? We show that answering this question reduces to solving an NP-hard combinatorial optimization problem which we call the edge ID problem. We propose efficient algorithms to approximate this problem, and evaluate our proposed algorithms against real-world networks and randomly generated graphs.

Learning Bayesian Networks in the Presence of Structural Side Information

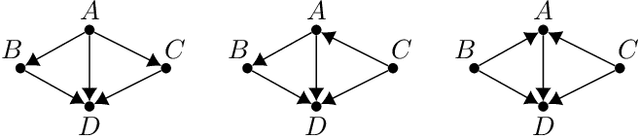
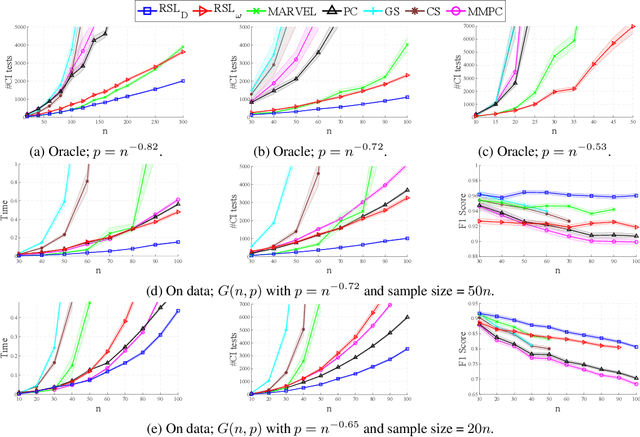
We study the problem of learning a Bayesian network (BN) of a set of variables when structural side information about the system is available. It is well known that learning the structure of a general BN is both computationally and statistically challenging. However, often in many applications, side information about the underlying structure can potentially reduce the learning complexity. In this paper, we develop a recursive constraint-based algorithm that efficiently incorporates such knowledge (i.e., side information) into the learning process. In particular, we study two types of structural side information about the underlying BN: (I) an upper bound on its clique number is known, or (II) it is diamond-free. We provide theoretical guarantees for the learning algorithms, including the worst-case number of tests required in each scenario. As a consequence of our work, we show that bounded treewidth BNs can be learned with polynomial complexity. Furthermore, we evaluate the performance and the scalability of our algorithms in both synthetic and real-world structures and show that they outperform the state-of-the-art structure learning algorithms.

Causal Effect Identification with Context-specific Independence Relations of Control Variables

We study the problem of causal effect identification from observational distribution given the causal graph and some context-specific independence (CSI) relations. It was recently shown that this problem is NP-hard, and while a sound algorithm to learn the causal effects is proposed in Tikka et al. (2019), no complete algorithm for the task exists. In this work, we propose a sound and complete algorithm for the setting when the CSI relations are limited to observed nodes with no parents in the causal graph. One limitation of the state of the art in terms of its applicability is that the CSI relations among all variables, even unobserved ones, must be given (as opposed to learned). Instead, We introduce a set of graphical constraints under which the CSI relations can be learned from mere observational distribution. This expands the set of identifiable causal effects beyond the state of the art.