CaTs and DAGs: Integrating Directed Acyclic Graphs with Transformers and Fully-Connected Neural Networks for Causally Constrained Predictions

Artificial Neural Networks (ANNs), including fully-connected networks and transformers, are highly flexible and powerful function approximators, widely applied in fields like computer vision and natural language processing. However, their inability to inherently respect causal structures can limit their robustness, making them vulnerable to covariate shift and difficult to interpret/explain. This poses significant challenges for their reliability in real-world applications. In this paper, we introduce Causal Fully-Connected Neural Networks (CFCNs) and Causal Transformers (CaTs), two general model families designed to operate under predefined causal constraints, as specified by a Directed Acyclic Graph (DAG). These models retain the powerful function approximation abilities of traditional neural networks while adhering to the underlying structural constraints, improving robustness, reliability, and interpretability at inference time. This approach opens new avenues for deploying neural networks in more demanding, real-world scenarios where robustness and explainability is critical.

psifx -- Psychological and Social Interactions Feature Extraction Package

psifx is a plug-and-play multi-modal feature extraction toolkit, aiming to facilitate and democratize the use of state-of-the-art machine learning techniques for human sciences research. It is motivated by a need (a) to automate and standardize data annotation processes, otherwise involving expensive, lengthy, and inconsistent human labor, such as the transcription or coding of behavior changes from audio and video sources; (b) to develop and distribute open-source community-driven psychology research software; and (c) to enable large-scale access and ease of use to non-expert users. The framework contains an array of tools for tasks, such as speaker diarization, closed-caption transcription and translation from audio, as well as body, hand, and facial pose estimation and gaze tracking from video. The package has been designed with a modular and task-oriented approach, enabling the community to add or update new tools easily. We strongly hope that this package will provide psychologists a simple and practical solution for efficiently a range of audio, linguistic, and visual features from audio and video, thereby creating new opportunities for in-depth study of real-time behavioral phenomena.

SLEM: Machine Learning for Path Modeling and Causal Inference with Super Learner Equation Modeling

Causal inference is a crucial goal of science, enabling researchers to arrive at meaningful conclusions regarding the predictions of hypothetical interventions using observational data. Path models, Structural Equation Models (SEMs), and, more generally, Directed Acyclic Graphs (DAGs), provide a means to unambiguously specify assumptions regarding the causal structure underlying a phenomenon. Unlike DAGs, which make very few assumptions about the functional and parametric form, SEM assumes linearity. This can result in functional misspecification which prevents researchers from undertaking reliable effect size estimation. In contrast, we propose Super Learner Equation Modeling, a path modeling technique integrating machine learning Super Learner ensembles. We empirically demonstrate its ability to provide consistent and unbiased estimates of causal effects, its competitive performance for linear models when compared with SEM, and highlight its superiority over SEM when dealing with non-linear relationships. We provide open-source code, and a tutorial notebook with example usage, accentuating the easy-to-use nature of the method.

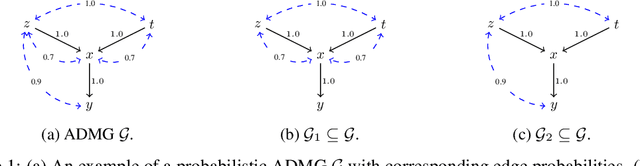
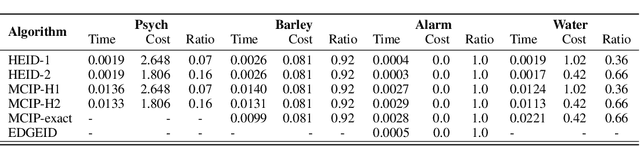
Causal Discovery in Probabilistic Networks with an Identifiable Causal Effect

Causal identification is at the core of the causal inference literature, where complete algorithms have been proposed to identify causal queries of interest. The validity of these algorithms hinges on the restrictive assumption of having access to a correctly specified causal structure. In this work, we study the setting where a probabilistic model of the causal structure is available. Specifically, the edges in a causal graph are assigned probabilities which may, for example, represent degree of belief from domain experts. Alternatively, the uncertainly about an edge may reflect the confidence of a particular statistical test. The question that naturally arises in this setting is: Given such a probabilistic graph and a specific causal effect of interest, what is the subgraph which has the highest plausibility and for which the causal effect is identifiable? We show that answering this question reduces to solving an NP-hard combinatorial optimization problem which we call the edge ID problem. We propose efficient algorithms to approximate this problem, and evaluate our proposed algorithms against real-world networks and randomly generated graphs.

A Causal Research Pipeline and Tutorial for Psychologists and Social Scientists

Causality is a fundamental part of the scientific endeavour to understand the world. Unfortunately, causality is still taboo in much of psychology and social science. Motivated by a growing number of recommendations for the importance of adopting causal approaches to research, we reformulate the typical approach to research in psychology to harmonize inevitably causal theories with the rest of the research pipeline. We present a new process which begins with the incorporation of techniques from the confluence of causal discovery and machine learning for the development, validation, and transparent formal specification of theories. We then present methods for reducing the complexity of the fully specified theoretical model into the fundamental submodel relevant to a given target hypothesis. From here, we establish whether or not the quantity of interest is estimable from the data, and if so, propose the use of semi-parametric machine learning methods for the estimation of causal effects. The overall goal is the presentation of a new research pipeline which can (a) facilitate scientific inquiry compatible with the desire to test causal theories (b) encourage transparent representation of our theories as unambiguous mathematical objects, (c) to tie our statistical models to specific attributes of the theory, thus reducing under-specification problems frequently resulting from the theory-to-model gap, and (d) to yield results and estimates which are causally meaningful and reproducible. The process is demonstrated through didactic examples with real-world data, and we conclude with a summary and discussion of limitations.

Trying to Outrun Causality with Machine Learning: Limitations of Model Explainability Techniques for Identifying Predictive Variables

Machine Learning explainability techniques have been proposed as a means of `explaining' or interrogating a model in order to understand why a particular decision or prediction has been made. Such an ability is especially important at a time when machine learning is being used to automate decision processes which concern sensitive factors and legal outcomes. Indeed, it is even a requirement according to EU law. Furthermore, researchers concerned with imposing overly restrictive functional form (e.g., as would be the case in a linear regression) may be motivated to use machine learning algorithms in conjunction with explainability techniques, as part of exploratory research, with the goal of identifying important variables which are associated with an outcome of interest. For example, epidemiologists might be interested in identifying `risk factors' - i.e. factors which affect recovery from disease - by using random forests and assessing variable relevance using importance measures. However, and as we demonstrate, machine learning algorithms are not as flexible as they might seem, and are instead incredibly sensitive to the underling causal structure in the data. The consequences of this are that predictors which are, in fact, critical to a causal system and highly correlated with the outcome, may nonetheless be deemed by explainability techniques to be unrelated/unimportant/unpredictive of the outcome. Rather than this being a limitation of explainability techniques per se, we show that it is rather a consequence of the mathematical implications of regression, and the interaction of these implications with the associated conditional independencies of the underlying causal structure. We provide some alternative recommendations for researchers wanting to explore the data for important variables.

A Free Lunch with Influence Functions? Improving Neural Network Estimates with Concepts from Semiparametric Statistics

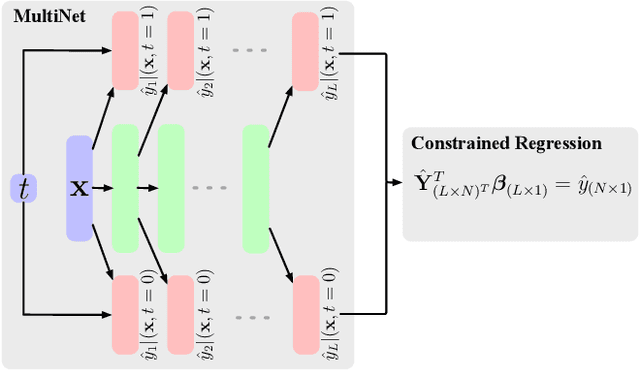
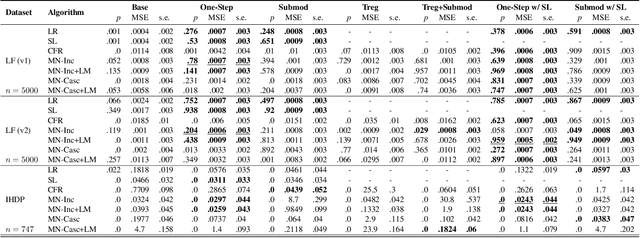
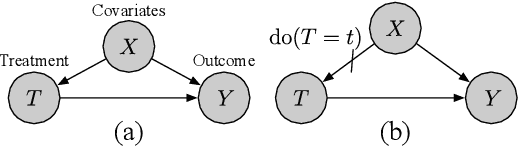
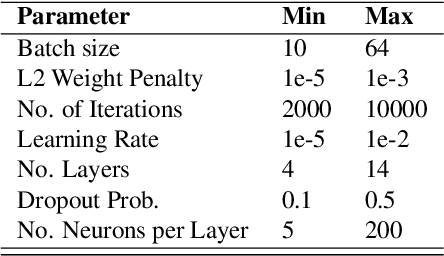
Parameter estimation in the empirical fields is usually undertaken using parametric models, and such models are convenient because they readily facilitate statistical inference. Unfortunately, they are unlikely to have a sufficiently flexible functional form to be able to adequately model real-world phenomena, and their usage may therefore result in biased estimates and invalid inference. Unfortunately, whilst non-parametric machine learning models may provide the needed flexibility to adapt to the complexity of real-world phenomena, they do not readily facilitate statistical inference, and may still exhibit residual bias. We explore the potential for semiparametric theory (in particular, the Influence Function) to be used to improve neural networks and machine learning algorithms in terms of (a) improving initial estimates without needing more data (b) increasing the robustness of our models, and (c) yielding confidence intervals for statistical inference. We propose a new neural network method MultiNet, which seeks the flexibility and diversity of an ensemble using a single architecture. Results on causal inference tasks indicate that MultiNet yields better performance than other approaches, and that all considered methods are amenable to improvement from semiparametric techniques under certain conditions. In other words, with these techniques we show that we can improve existing neural networks for `free', without needing more data, and without needing to retrain them. Finally, we provide the expression for deriving influence functions for estimands from a general graph, and the code to do so automatically.

Shadow-Mapping for Unsupervised Neural Causal Discovery

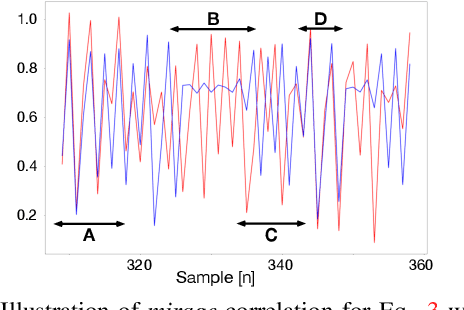
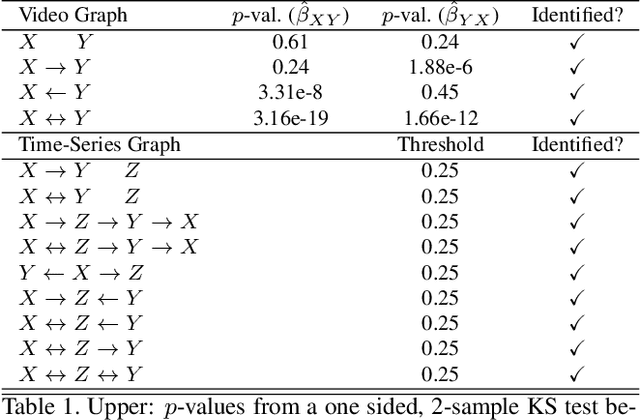
An important goal across most scientific fields is the discovery of causal structures underling a set of observations. Unfortunately, causal discovery methods which are based on correlation or mutual information can often fail to identify causal links in systems which exhibit dynamic relationships. Such dynamic systems (including the famous coupled logistic map) exhibit `mirage' correlations which appear and disappear depending on the observation window. This means not only that correlation is not causation but, perhaps counter-intuitively, that causation may occur without correlation. In this paper we describe Neural Shadow-Mapping, a neural network based method which embeds high-dimensional video data into a low-dimensional shadow representation, for subsequent estimation of causal links. We demonstrate its performance at discovering causal links from video-representations of dynamic systems.

VDSM: Unsupervised Video Disentanglement with State-Space Modeling and Deep Mixtures of Experts

Disentangled representations support a range of downstream tasks including causal reasoning, generative modeling, and fair machine learning. Unfortunately, disentanglement has been shown to be impossible without the incorporation of supervision or inductive bias. Given that supervision is often expensive or infeasible to acquire, we choose to incorporate structural inductive bias and present an unsupervised, deep State-Space-Model for Video Disentanglement (VDSM). The model disentangles latent time-varying and dynamic factors via the incorporation of hierarchical structure with a dynamic prior and a Mixture of Experts decoder. VDSM learns separate disentangled representations for the identity of the object or person in the video, and for the action being performed. We evaluate VDSM across a range of qualitative and quantitative tasks including identity and dynamics transfer, sequence generation, Fr\'echet Inception Distance, and factor classification. VDSM provides state-of-the-art performance and exceeds adversarial methods, even when the methods use additional supervision.

D'ya like DAGs? A Survey on Structure Learning and Causal Discovery

Causal reasoning is a crucial part of science and human intelligence. In order to discover causal relationships from data, we need structure discovery methods. We provide a review of background theory and a survey of methods for structure discovery. We primarily focus on modern, continuous optimization methods, and provide reference to further resources such as benchmark datasets and software packages. Finally, we discuss the assumptive leap required to take us from structure to causality.