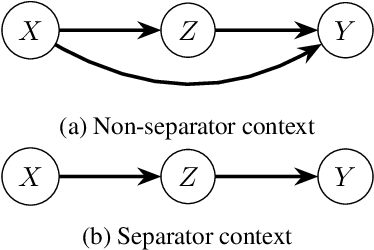
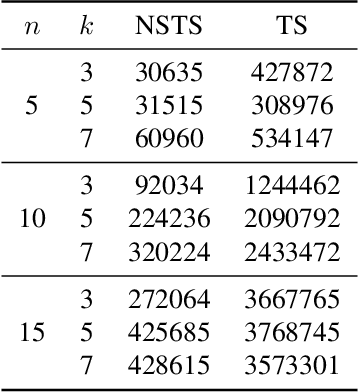
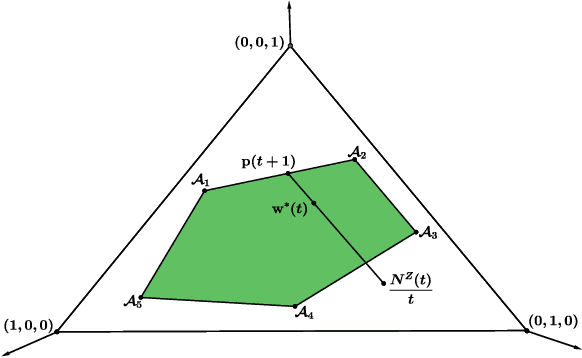
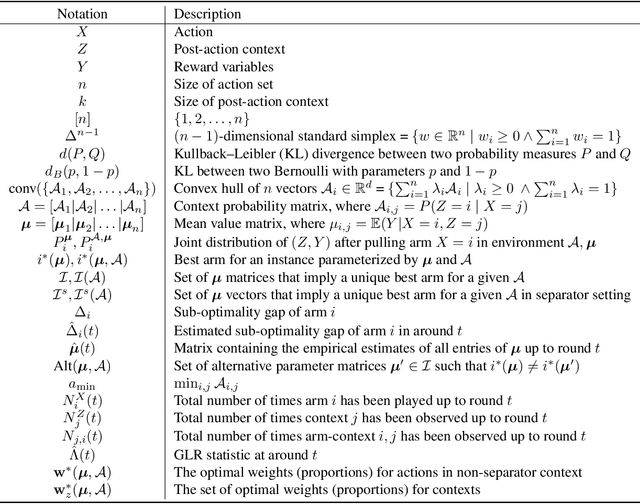
Optimal Best Arm Identification with Post-Action Context

We introduce the problem of best arm identification (BAI) with post-action context, a new BAI problem in a stochastic multi-armed bandit environment and the fixed-confidence setting. The problem addresses the scenarios in which the learner receives a $\textit{post-action context}$ in addition to the reward after playing each action. This post-action context provides additional information that can significantly facilitate the decision process. We analyze two different types of the post-action context: (i) $\textit{non-separator}$, where the reward depends on both the action and the context, and (ii) $\textit{separator}$, where the reward depends solely on the context. For both cases, we derive instance-dependent lower bounds on the sample complexity and propose algorithms that asymptotically achieve the optimal sample complexity. For the non-separator setting, we do so by demonstrating that the Track-and-Stop algorithm can be extended to this setting. For the separator setting, we propose a novel sampling rule called $\textit{G-tracking}$, which uses the geometry of the context space to directly track the contexts rather than the actions. Finally, our empirical results showcase the advantage of our approaches compared to the state of the art.

Causal Effect Identification in a Sub-Population with Latent Variables

The s-ID problem seeks to compute a causal effect in a specific sub-population from the observational data pertaining to the same sub population (Abouei et al., 2023). This problem has been addressed when all the variables in the system are observable. In this paper, we consider an extension of the s-ID problem that allows for the presence of latent variables. To tackle the challenges induced by the presence of latent variables in a sub-population, we first extend the classical relevant graphical definitions, such as c-components and Hedges, initially defined for the so-called ID problem (Pearl, 1995; Tian & Pearl, 2002), to their new counterparts. Subsequently, we propose a sound algorithm for the s-ID problem with latent variables.

s-ID: Causal Effect Identification in a Sub-Population

Causal inference in a sub-population involves identifying the causal effect of an intervention on a specific subgroup within a larger population. However, ignoring the subtleties introduced by sub-populations can either lead to erroneous inference or limit the applicability of existing methods. We introduce and advocate for a causal inference problem in sub-populations (henceforth called s-ID), in which we merely have access to observational data of the targeted sub-population (as opposed to the entire population). Existing inference problems in sub-populations operate on the premise that the given data distributions originate from the entire population, thus, cannot tackle the s-ID problem. To address this gap, we provide necessary and sufficient conditions that must hold in the causal graph for a causal effect in a sub-population to be identifiable from the observational distribution of that sub-population. Given these conditions, we present a sound and complete algorithm for the s-ID problem.

The Interplay between Distribution Parameters and the Accuracy-Robustness Tradeoff in Classification

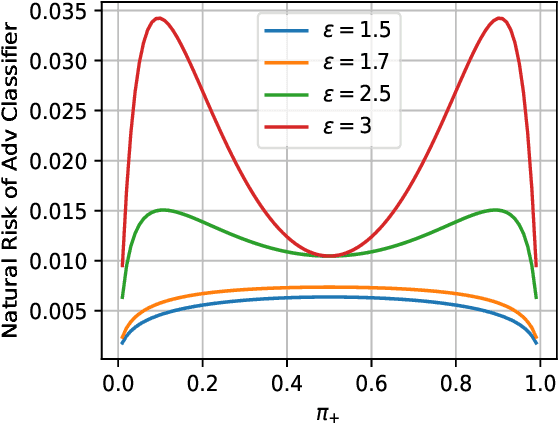
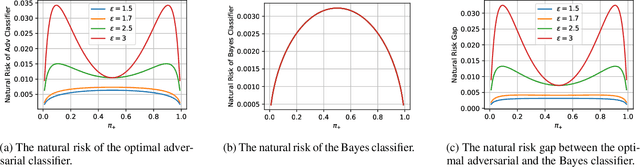
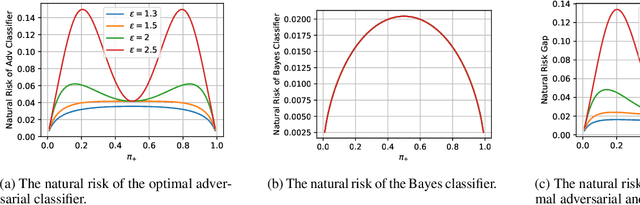
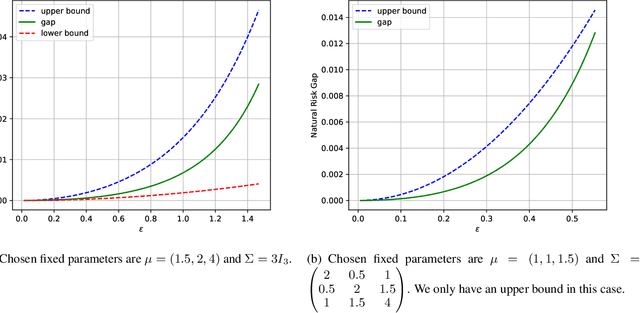
Adversarial training tends to result in models that are less accurate on natural (unperturbed) examples compared to standard models. This can be attributed to either an algorithmic shortcoming or a fundamental property of the training data distribution, which admits different solutions for optimal standard and adversarial classifiers. In this work, we focus on the latter case under a binary Gaussian mixture classification problem. Unlike earlier work, we aim to derive the natural accuracy gap between the optimal Bayes and adversarial classifiers, and study the effect of different distributional parameters, namely separation between class centroids, class proportions, and the covariance matrix, on the derived gap. We show that under certain conditions, the natural error of the optimal adversarial classifier, as well as the gap, are locally minimized when classes are balanced, contradicting the performance of the Bayes classifier where perfect balance induces the worst accuracy. Moreover, we show that with an $\ell_\infty$ bounded perturbation and an adversarial budget of $\epsilon$, this gap is $\Theta(\epsilon^2)$ for the worst-case parameters, which for suitably small $\epsilon$ indicates the theoretical possibility of achieving robust classifiers with near-perfect accuracy, which is rarely reflected in practical algorithms.