Soft Preference Optimization: Aligning Language Models to Expert Distributions

We propose Soft Preference Optimization (SPO), a method for aligning generative models, such as Large Language Models (LLMs), with human preferences, without the need for a reward model. SPO optimizes model outputs directly over a preference dataset through a natural loss function that integrates preference loss with a regularization term across the model's entire output distribution rather than limiting it to the preference dataset. Although SPO does not require the assumption of an existing underlying reward model, we demonstrate that, under the Bradley-Terry (BT) model assumption, it converges to a softmax of scaled rewards, with the distribution's "softness" adjustable via the softmax exponent, an algorithm parameter. We showcase SPO's methodology, its theoretical foundation, and its comparative advantages in simplicity, computational efficiency, and alignment precision.

MetaOptimize: A Framework for Optimizing Step Sizes and Other Meta-parameters

This paper addresses the challenge of optimizing meta-parameters (i.e., hyperparameters) in machine learning algorithms, a critical factor influencing training efficiency and model performance. Moving away from the computationally expensive traditional meta-parameter search methods, we introduce MetaOptimize framework that dynamically adjusts meta-parameters, particularly step sizes (also known as learning rates), during training. More specifically, MetaOptimize can wrap around any first-order optimization algorithm, tuning step sizes on the fly to minimize a specific form of regret that accounts for long-term effect of step sizes on training, through a discounted sum of future losses. We also introduce low complexity variants of MetaOptimize that, in conjunction with its adaptability to multiple optimization algorithms, demonstrate performance competitive to those of best hand-crafted learning rate schedules across various machine learning applications.

Step-size Optimization for Continual Learning

In continual learning, a learner has to keep learning from the data over its whole life time. A key issue is to decide what knowledge to keep and what knowledge to let go. In a neural network, this can be implemented by using a step-size vector to scale how much gradient samples change network weights. Common algorithms, like RMSProp and Adam, use heuristics, specifically normalization, to adapt this step-size vector. In this paper, we show that those heuristics ignore the effect of their adaptation on the overall objective function, for example by moving the step-size vector away from better step-size vectors. On the other hand, stochastic meta-gradient descent algorithms, like IDBD (Sutton, 1992), explicitly optimize the step-size vector with respect to the overall objective function. On simple problems, we show that IDBD is able to consistently improve step-size vectors, where RMSProp and Adam do not. We explain the differences between the two approaches and their respective limitations. We conclude by suggesting that combining both approaches could be a promising future direction to improve the performance of neural networks in continual learning.

Toward Efficient Gradient-Based Value Estimation

Gradient-based methods for value estimation in reinforcement learning have favorable stability properties, but they are typically much slower than Temporal Difference (TD) learning methods. We study the root causes of this slowness and show that Mean Square Bellman Error (MSBE) is an ill-conditioned loss function in the sense that its Hessian has large condition-number. To resolve the adverse effect of poor conditioning of MSBE on gradient based methods, we propose a low complexity batch-free proximal method that approximately follows the Gauss-Newton direction and is asymptotically robust to parameterization. Our main algorithm, called RANS, is efficient in the sense that it is significantly faster than the residual gradient methods while having almost the same computational complexity, and is competitive with TD on the classic problems that we tested.

Order Optimal One-Shot Federated Learning for non-Convex Loss Functions

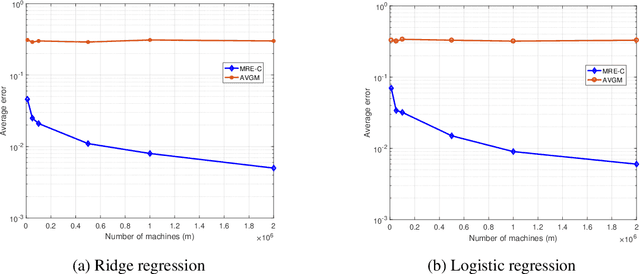
We consider the problem of federated learning in a one-shot setting in which there are $m$ machines, each observing $n$ samples function from an unknown distribution on non-convex loss functions. Let $F:[-1,1]^d\to\mathbb{R}$ be the expected loss function with respect to this unknown distribution. The goal is to find an estimate of the minimizer of $F$. Based on its observations, each machine generates a signal of bounded length $B$ and sends it to a server. The sever collects signals of all machines and outputs an estimate of the minimizer of $F$. We propose a distributed learning algorithm, called Multi-Resolution Estimator for Non-Convex loss function (MRE-NC), whose expected error is bounded by $\max\big(1/\sqrt{n}(mB)^{1/d}, 1/\sqrt{mn}\big)$, up to polylogarithmic factors. We also provide a matching lower bound on the performance of any algorithm, showing that MRE-NC is order optimal in terms of $n$ and $m$. Experiments on synthetic and real data show the effectiveness of MRE-NC in distributed learning of model's parameters for non-convex loss functions.

Order Optimal One-Shot Distributed Learning

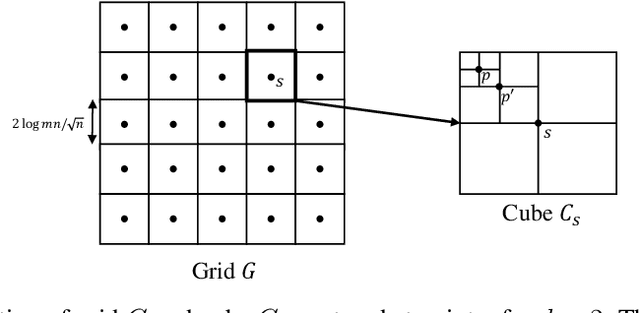
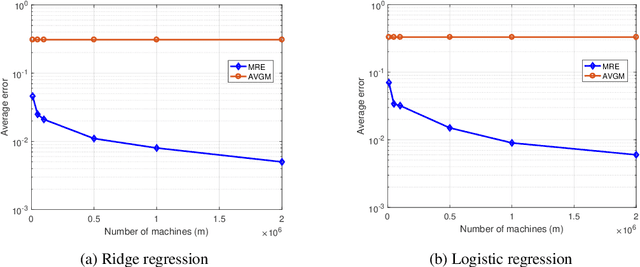
We consider distributed statistical optimization in one-shot setting, where there are $m$ machines each observing $n$ i.i.d. samples. Based on its observed samples, each machine then sends an $O(\log(mn))$-length message to a server, at which a parameter minimizing an expected loss is to be estimated. We propose an algorithm called Multi-Resolution Estimator (MRE) whose expected error is no larger than $\tilde{O}\big(m^{-{1}/{\max(d,2)}} n^{-1/2}\big)$, where $d$ is the dimension of the parameter space. This error bound meets existing lower bounds up to poly-logarithmic factors, and is thereby order optimal. The expected error of MRE, unlike existing algorithms, tends to zero as the number of machines ($m$) goes to infinity, even when the number of samples per machine ($n$) remains upper bounded by a constant. This property of the MRE algorithm makes it applicable in new machine learning paradigms where $m$ is much larger than $n$.

Theoretical Limits of One-Shot Distributed Learning

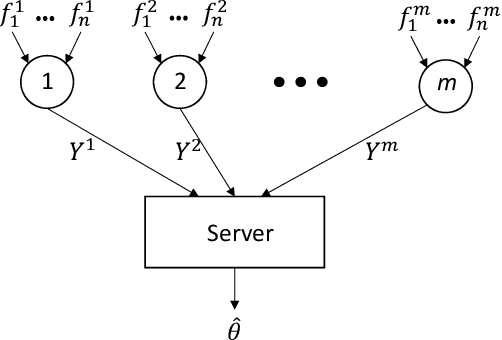
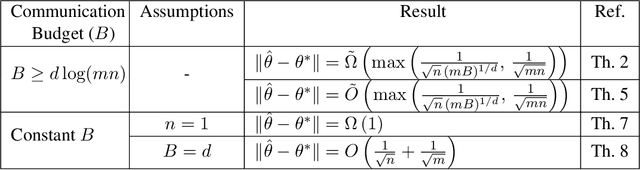
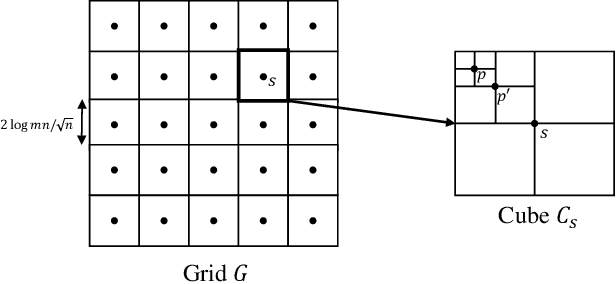
We consider a distributed system of $m$ machines and a server. Each machine draws $n$ i.i.d samples from an unknown distribution and sends a message of bounded length $b$ to the server. The server then collects messages from all machines and estimates a parameter that minimizes an expected loss. We investigate the impact of communication constraint, $b$, on the expected error; and derive lower bounds on the best error achievable by any algorithm. As our main result, for general values of $b$, we establish a $\tilde{\Omega}\big( (mb)^{-{1}/{\max(d,2)}} n^{-1/2} \big)$ lower bounded on the expected error, where $d$ is the dimension of the parameter space. Moreover, for constant values of $b$ and under the extra assumption $n=1$, we show that expected error remains lower bounded by a constant, even when $m$ tends to infinity.