Theoretical Limits of One-Shot Distributed Learning

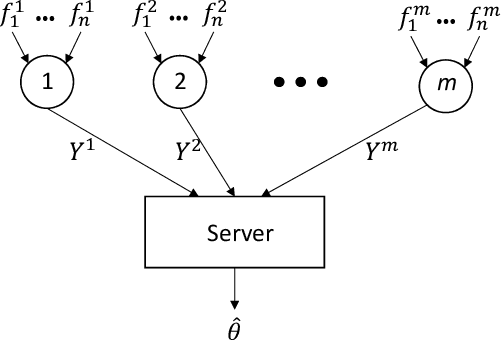
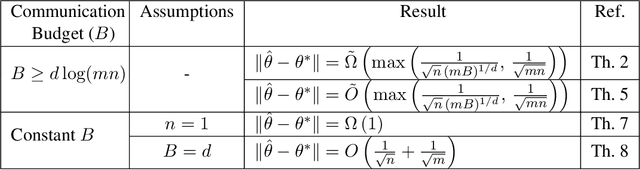
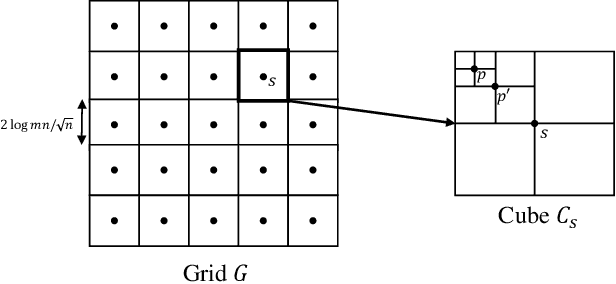
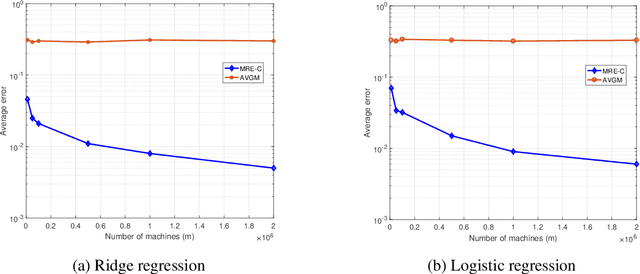
We consider a distributed system of $m$ machines and a server. Each machine draws $n$ i.i.d samples from an unknown distribution and sends a message of bounded length $b$ to the server. The server then collects messages from all machines and estimates a parameter that minimizes an expected loss. We investigate the impact of communication constraint, $b$, on the expected error; and derive lower bounds on the best error achievable by any algorithm. As our main result, for general values of $b$, we establish a $\tilde{\Omega}\big( (mb)^{-{1}/{\max(d,2)}} n^{-1/2} \big)$ lower bounded on the expected error, where $d$ is the dimension of the parameter space. Moreover, for constant values of $b$ and under the extra assumption $n=1$, we show that expected error remains lower bounded by a constant, even when $m$ tends to infinity.