Order Optimal One-Shot Federated Learning for non-Convex Loss Functions

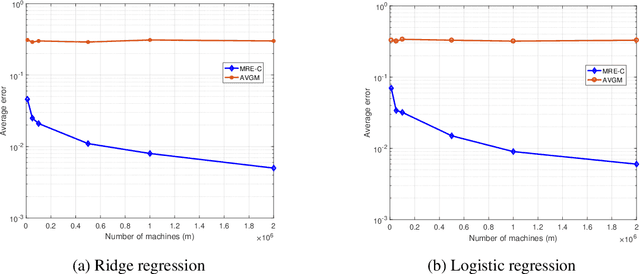
We consider the problem of federated learning in a one-shot setting in which there are $m$ machines, each observing $n$ samples function from an unknown distribution on non-convex loss functions. Let $F:[-1,1]^d\to\mathbb{R}$ be the expected loss function with respect to this unknown distribution. The goal is to find an estimate of the minimizer of $F$. Based on its observations, each machine generates a signal of bounded length $B$ and sends it to a server. The sever collects signals of all machines and outputs an estimate of the minimizer of $F$. We propose a distributed learning algorithm, called Multi-Resolution Estimator for Non-Convex loss function (MRE-NC), whose expected error is bounded by $\max\big(1/\sqrt{n}(mB)^{1/d}, 1/\sqrt{mn}\big)$, up to polylogarithmic factors. We also provide a matching lower bound on the performance of any algorithm, showing that MRE-NC is order optimal in terms of $n$ and $m$. Experiments on synthetic and real data show the effectiveness of MRE-NC in distributed learning of model's parameters for non-convex loss functions.

Order Optimal One-Shot Distributed Learning

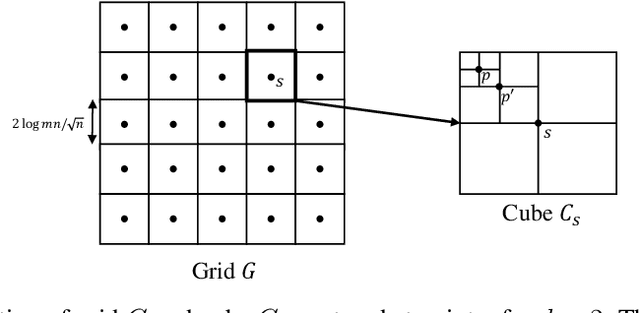
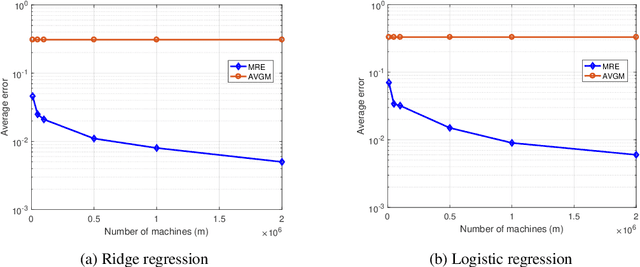
We consider distributed statistical optimization in one-shot setting, where there are $m$ machines each observing $n$ i.i.d. samples. Based on its observed samples, each machine then sends an $O(\log(mn))$-length message to a server, at which a parameter minimizing an expected loss is to be estimated. We propose an algorithm called Multi-Resolution Estimator (MRE) whose expected error is no larger than $\tilde{O}\big(m^{-{1}/{\max(d,2)}} n^{-1/2}\big)$, where $d$ is the dimension of the parameter space. This error bound meets existing lower bounds up to poly-logarithmic factors, and is thereby order optimal. The expected error of MRE, unlike existing algorithms, tends to zero as the number of machines ($m$) goes to infinity, even when the number of samples per machine ($n$) remains upper bounded by a constant. This property of the MRE algorithm makes it applicable in new machine learning paradigms where $m$ is much larger than $n$.

Theoretical Limits of One-Shot Distributed Learning

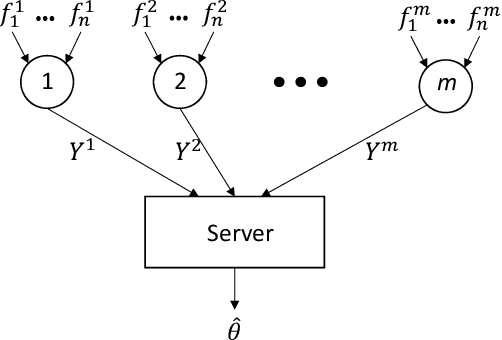
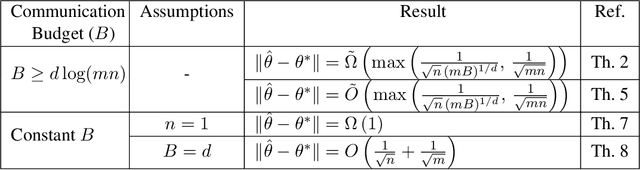
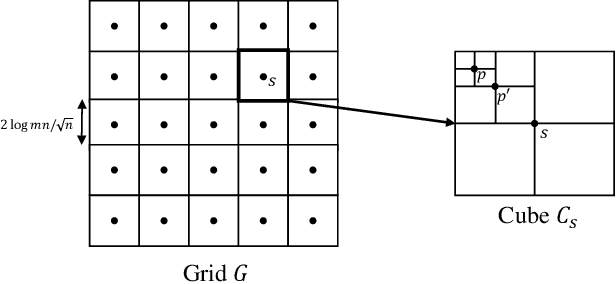
We consider a distributed system of $m$ machines and a server. Each machine draws $n$ i.i.d samples from an unknown distribution and sends a message of bounded length $b$ to the server. The server then collects messages from all machines and estimates a parameter that minimizes an expected loss. We investigate the impact of communication constraint, $b$, on the expected error; and derive lower bounds on the best error achievable by any algorithm. As our main result, for general values of $b$, we establish a $\tilde{\Omega}\big( (mb)^{-{1}/{\max(d,2)}} n^{-1/2} \big)$ lower bounded on the expected error, where $d$ is the dimension of the parameter space. Moreover, for constant values of $b$ and under the extra assumption $n=1$, we show that expected error remains lower bounded by a constant, even when $m$ tends to infinity.

Distributed Voting/Ranking with Optimal Number of States per Node

Considering a network with $n$ nodes, where each node initially votes for one (or more) choices out of $K$ possible choices, we present a Distributed Multi-choice Voting/Ranking (DMVR) algorithm to determine either the choice with maximum vote (the voting problem) or to rank all the choices in terms of their acquired votes (the ranking problem). The algorithm consolidates node votes across the network by updating the states of interacting nodes using two key operations, the union and the intersection. The proposed algorithm is simple, independent from network size, and easily scalable in terms of the number of choices $K$, using only $K\times 2^{K-1}$ nodal states for voting, and $K\times K!$ nodal states for ranking. We prove the number of states to be optimal in the ranking case, this optimality is conjectured to also apply to the voting case. The time complexity of the algorithm is analyzed in complete graphs. We show that the time complexity for both ranking and voting is $O(\log(n))$ for given vote percentages, and is inversely proportional to the minimum of the vote percentage differences among various choices.

Token-based Function Computation with Memory

In distributed function computation, each node has an initial value and the goal is to compute a function of these values in a distributed manner. In this paper, we propose a novel token-based approach to compute a wide class of target functions to which we refer as "Token-based function Computation with Memory" (TCM) algorithm. In this approach, node values are attached to tokens and travel across the network. Each pair of travelling tokens would coalesce when they meet, forming a token with a new value as a function of the original token values. In contrast to the Coalescing Random Walk (CRW) algorithm, where token movement is governed by random walk, meeting of tokens in our scheme is accelerated by adopting a novel chasing mechanism. We proved that, compared to the CRW algorithm, the TCM algorithm results in a reduction of time complexity by a factor of at least $\sqrt{n/\log(n)}$ in Erd\"os-Renyi and complete graphs, and by a factor of $\log(n)/\log(\log(n))$ in torus networks. Simulation results show that there is at least a constant factor improvement in the message complexity of TCM algorithm in all considered topologies. Robustness of the CRW and TCM algorithms in the presence of node failure is analyzed. We show that their robustness can be improved by running multiple instances of the algorithms in parallel.