Neural Causal Abstractions

The abilities of humans to understand the world in terms of cause and effect relationships, as well as to compress information into abstract concepts, are two hallmark features of human intelligence. These two topics have been studied in tandem in the literature under the rubric of causal abstractions theory. In practice, it remains an open problem how to best leverage abstraction theory in real-world causal inference tasks, where the true mechanisms are unknown and only limited data is available. In this paper, we develop a new family of causal abstractions by clustering variables and their domains. This approach refines and generalizes previous notions of abstractions to better accommodate individual causal distributions that are spawned by Pearl's causal hierarchy. We show that such abstractions are learnable in practical settings through Neural Causal Models (Xia et al., 2021), enabling the use of the deep learning toolkit to solve various challenging causal inference tasks -- identification, estimation, sampling -- at different levels of granularity. Finally, we integrate these results with representation learning to create more flexible abstractions, moving these results closer to practical applications. Our experiments support the theory and illustrate how to scale causal inferences to high-dimensional settings involving image data.

Neural Causal Models for Counterfactual Identification and Estimation

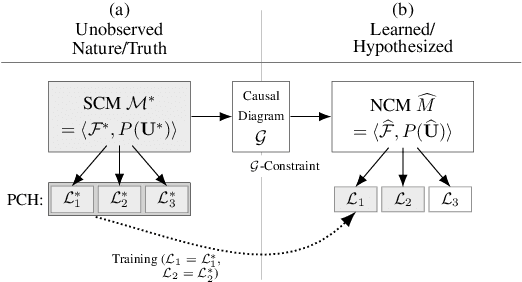
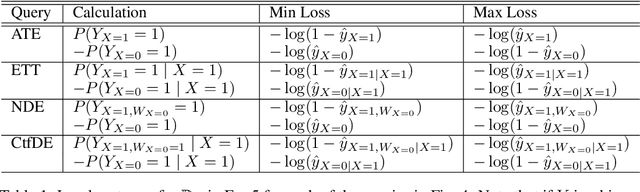
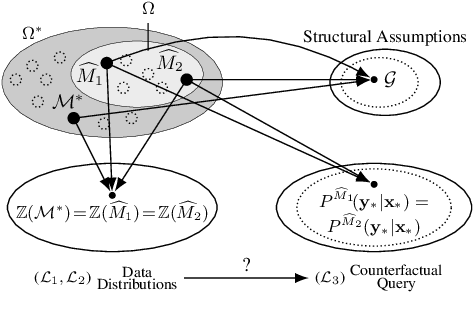
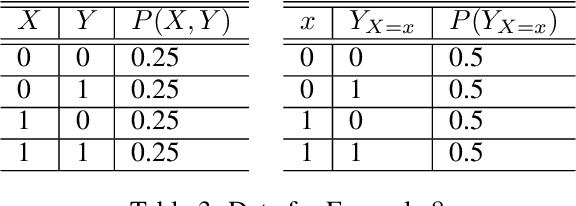
Evaluating hypothetical statements about how the world would be had a different course of action been taken is arguably one key capability expected from modern AI systems. Counterfactual reasoning underpins discussions in fairness, the determination of blame and responsibility, credit assignment, and regret. In this paper, we study the evaluation of counterfactual statements through neural models. Specifically, we tackle two causal problems required to make such evaluations, i.e., counterfactual identification and estimation from an arbitrary combination of observational and experimental data. First, we show that neural causal models (NCMs) are expressive enough and encode the structural constraints necessary for performing counterfactual reasoning. Second, we develop an algorithm for simultaneously identifying and estimating counterfactual distributions. We show that this algorithm is sound and complete for deciding counterfactual identification in general settings. Third, considering the practical implications of these results, we introduce a new strategy for modeling NCMs using generative adversarial networks. Simulations corroborate with the proposed methodology.

Causal Transportability for Visual Recognition

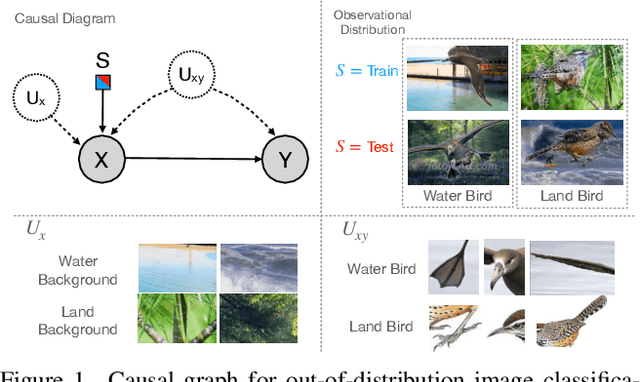
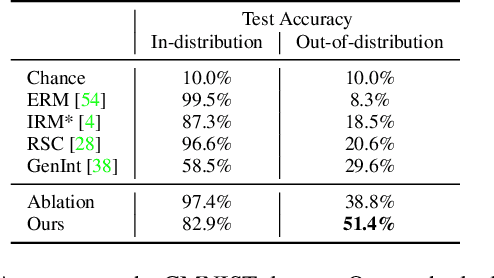
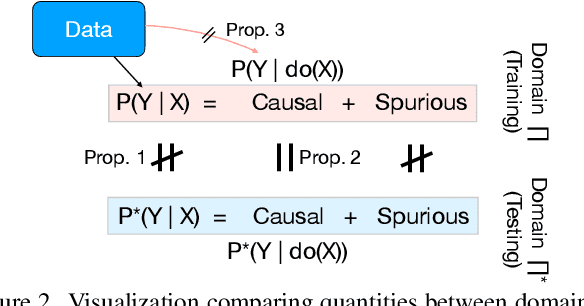
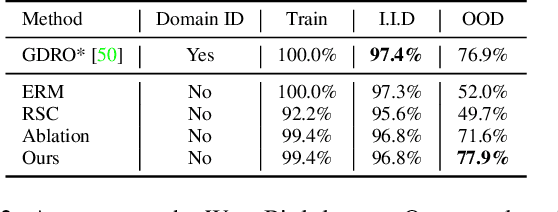
Visual representations underlie object recognition tasks, but they often contain both robust and non-robust features. Our main observation is that image classifiers may perform poorly on out-of-distribution samples because spurious correlations between non-robust features and labels can be changed in a new environment. By analyzing procedures for out-of-distribution generalization with a causal graph, we show that standard classifiers fail because the association between images and labels is not transportable across settings. However, we then show that the causal effect, which severs all sources of confounding, remains invariant across domains. This motivates us to develop an algorithm to estimate the causal effect for image classification, which is transportable (i.e., invariant) across source and target environments. Without observing additional variables, we show that we can derive an estimand for the causal effect under empirical assumptions using representations in deep models as proxies. Theoretical analysis, empirical results, and visualizations show that our approach captures causal invariances and improves overall generalization.

The Causal-Neural Connection: Expressiveness, Learnability, and Inference

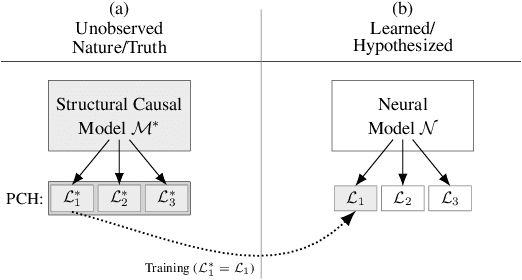
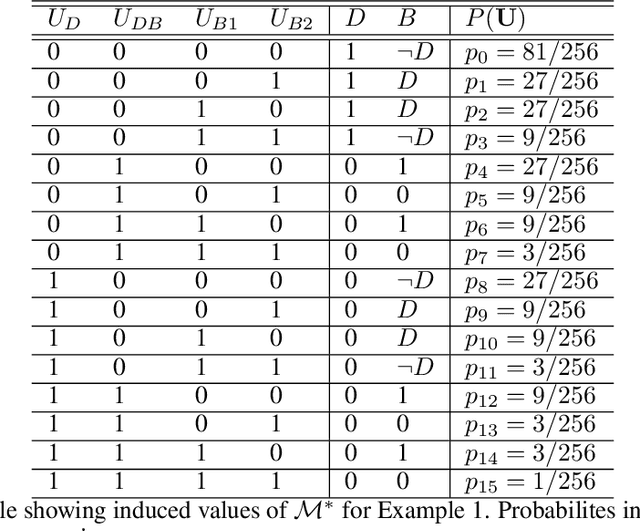
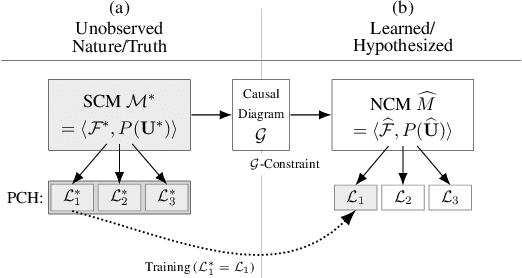
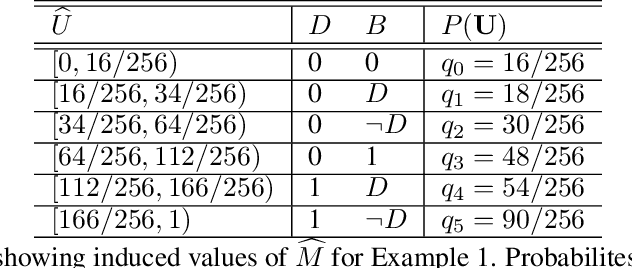
One of the central elements of any causal inference is an object called structural causal model (SCM), which represents a collection of mechanisms and exogenous sources of random variation of the system under investigation (Pearl, 2000). An important property of many kinds of neural networks is universal approximability: the ability to approximate any function to arbitrary precision. Given this property, one may be tempted to surmise that a collection of neural nets is capable of learning any SCM by training on data generated by that SCM. In this paper, we show this is not the case by disentangling the notions of expressivity and learnability. Specifically, we show that the causal hierarchy theorem (Thm. 1, Bareinboim et al., 2020), which describes the limits of what can be learned from data, still holds for neural models. For instance, an arbitrarily complex and expressive neural net is unable to predict the effects of interventions given observational data alone. Given this result, we introduce a special type of SCM called a neural causal model (NCM), and formalize a new type of inductive bias to encode structural constraints necessary for performing causal inferences. Building on this new class of models, we focus on solving two canonical tasks found in the literature known as causal identification and estimation. Leveraging the neural toolbox, we develop an algorithm that is both sufficient and necessary to determine whether a causal effect can be learned from data (i.e., causal identifiability); it then estimates the effect whenever identifiability holds (causal estimation). Simulations corroborate the proposed approach.