Kai-Zhan Lee
The Causal-Neural Connection: Expressiveness, Learnability, and Inference
Jul 14, 2021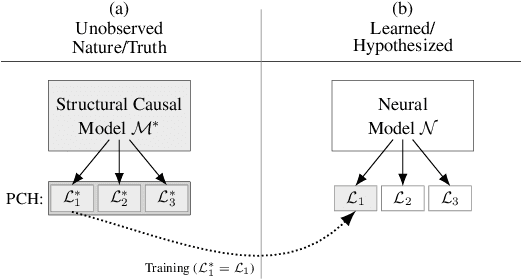
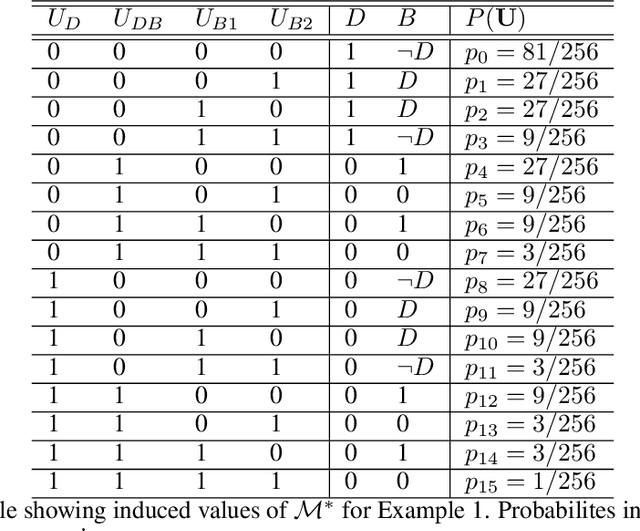
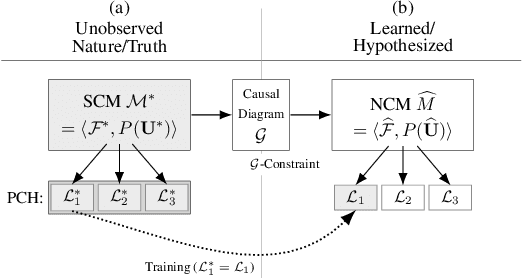
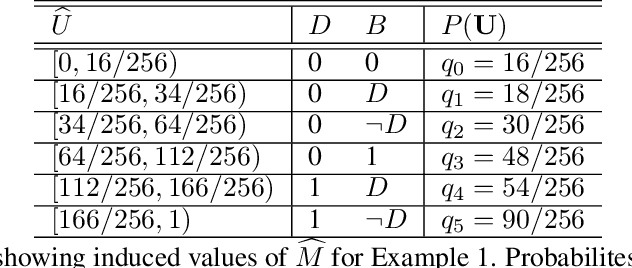
Abstract:One of the central elements of any causal inference is an object called structural causal model (SCM), which represents a collection of mechanisms and exogenous sources of random variation of the system under investigation (Pearl, 2000). An important property of many kinds of neural networks is universal approximability: the ability to approximate any function to arbitrary precision. Given this property, one may be tempted to surmise that a collection of neural nets is capable of learning any SCM by training on data generated by that SCM. In this paper, we show this is not the case by disentangling the notions of expressivity and learnability. Specifically, we show that the causal hierarchy theorem (Thm. 1, Bareinboim et al., 2020), which describes the limits of what can be learned from data, still holds for neural models. For instance, an arbitrarily complex and expressive neural net is unable to predict the effects of interventions given observational data alone. Given this result, we introduce a special type of SCM called a neural causal model (NCM), and formalize a new type of inductive bias to encode structural constraints necessary for performing causal inferences. Building on this new class of models, we focus on solving two canonical tasks found in the literature known as causal identification and estimation. Leveraging the neural toolbox, we develop an algorithm that is both sufficient and necessary to determine whether a causal effect can be learned from data (i.e., causal identifiability); it then estimates the effect whenever identifiability holds (causal estimation). Simulations corroborate the proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge