Continuous-Time Digital Twin with Analogue Memristive Neural Ordinary Differential Equation Solver

Digital twins, the cornerstone of Industry 4.0, replicate real-world entities through computer models, revolutionising fields such as manufacturing management and industrial automation. Recent advances in machine learning provide data-driven methods for developing digital twins using discrete-time data and finite-depth models on digital computers. However, this approach fails to capture the underlying continuous dynamics and struggles with modelling complex system behaviour. Additionally, the architecture of digital computers, with separate storage and processing units, necessitates frequent data transfers and Analogue-Digital (A/D) conversion, thereby significantly increasing both time and energy costs. Here, we introduce a memristive neural ordinary differential equation (ODE) solver for digital twins, which is capable of capturing continuous-time dynamics and facilitates the modelling of complex systems using an infinite-depth model. By integrating storage and computation within analogue memristor arrays, we circumvent the von Neumann bottleneck, thus enhancing both speed and energy efficiency. We experimentally validate our approach by developing a digital twin of the HP memristor, which accurately extrapolates its nonlinear dynamics, achieving a 4.2-fold projected speedup and a 41.4-fold projected decrease in energy consumption compared to state-of-the-art digital hardware, while maintaining an acceptable error margin. Additionally, we demonstrate scalability through experimentally grounded simulations of Lorenz96 dynamics, exhibiting projected performance improvements of 12.6-fold in speed and 189.7-fold in energy efficiency relative to traditional digital approaches. By harnessing the capabilities of fully analogue computing, our breakthrough accelerates the development of digital twins, offering an efficient and rapid solution to meet the demands of Industry 4.0.

Modeling High-Dimensional Data with Unknown Cut Points: A Fusion Penalized Logistic Threshold Regression

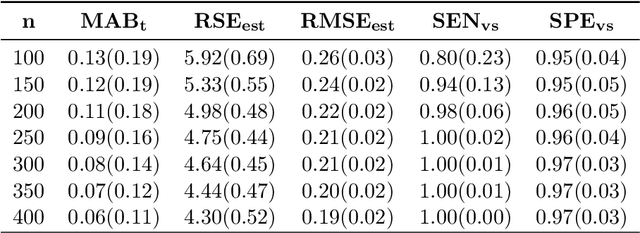
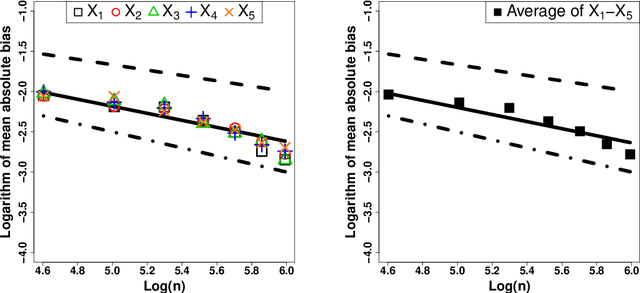
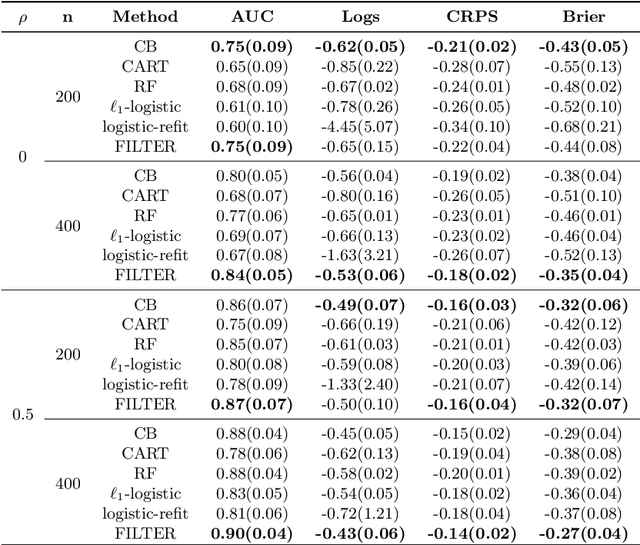
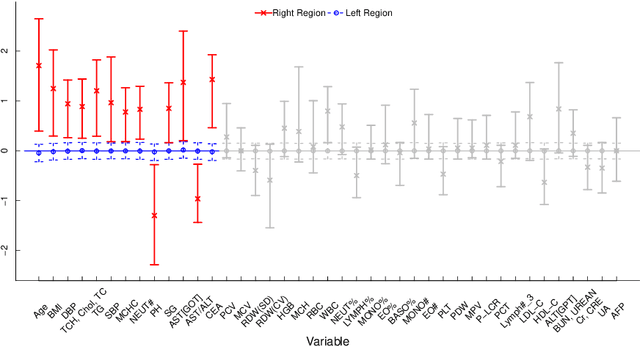
In traditional logistic regression models, the link function is often assumed to be linear and continuous in predictors. Here, we consider a threshold model that all continuous features are discretized into ordinal levels, which further determine the binary responses. Both the threshold points and regression coefficients are unknown and to be estimated. For high dimensional data, we propose a fusion penalized logistic threshold regression (FILTER) model, where a fused lasso penalty is employed to control the total variation and shrink the coefficients to zero as a method of variable selection. Under mild conditions on the estimate of unknown threshold points, we establish the non-asymptotic error bound for coefficient estimation and the model selection consistency. With a careful characterization of the error propagation, we have also shown that the tree-based method, such as CART, fulfill the threshold estimation conditions. We find the FILTER model is well suited in the problem of early detection and prediction for chronic disease like diabetes, using physical examination data. The finite sample behavior of our proposed method are also explored and compared with extensive Monte Carlo studies, which supports our theoretical discoveries.