Uncertainty Modeling in Graph Neural Networks via Stochastic Differential Equations

We address the problem of learning uncertainty-aware representations for graph-structured data. While Graph Neural Ordinary Differential Equations (GNODE) are effective in learning node representations, they fail to quantify uncertainty. To address this, we introduce Latent Graph Neural Stochastic Differential Equations (LGNSDE), which enhance GNODE by embedding randomness through Brownian motion to quantify uncertainty. We provide theoretical guarantees for LGNSDE and empirically show better performance in uncertainty quantification.

Feature Attribution with Necessity and Sufficiency via Dual-stage Perturbation Test for Causal Explanation

We investigate the problem of explainability in machine learning.To address this problem, Feature Attribution Methods (FAMs) measure the contribution of each feature through a perturbation test, where the difference in prediction is compared under different perturbations.However, such perturbation tests may not accurately distinguish the contributions of different features, when their change in prediction is the same after perturbation.In order to enhance the ability of FAMs to distinguish different features' contributions in this challenging setting, we propose to utilize the probability (PNS) that perturbing a feature is a necessary and sufficient cause for the prediction to change as a measure of feature importance.Our approach, Feature Attribution with Necessity and Sufficiency (FANS), computes the PNS via a perturbation test involving two stages (factual and interventional).In practice, to generate counterfactual samples, we use a resampling-based approach on the observed samples to approximate the required conditional distribution.Finally, we combine FANS and gradient-based optimization to extract the subset with the largest PNS.We demonstrate that FANS outperforms existing feature attribution methods on six benchmarks.

Graph Neural Stochastic Differential Equations

We present a novel model Graph Neural Stochastic Differential Equations (Graph Neural SDEs). This technique enhances the Graph Neural Ordinary Differential Equations (Graph Neural ODEs) by embedding randomness into data representation using Brownian motion. This inclusion allows for the assessment of prediction uncertainty, a crucial aspect frequently missed in current models. In our framework, we spotlight the \textit{Latent Graph Neural SDE} variant, demonstrating its effectiveness. Through empirical studies, we find that Latent Graph Neural SDEs surpass conventional models like Graph Convolutional Networks and Graph Neural ODEs, especially in confidence prediction, making them superior in handling out-of-distribution detection across both static and spatio-temporal contexts.

Large-Scale Educational Question Analysis with Partial Variational Auto-encoders

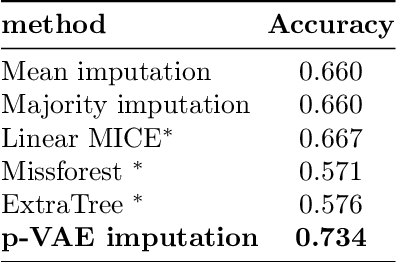
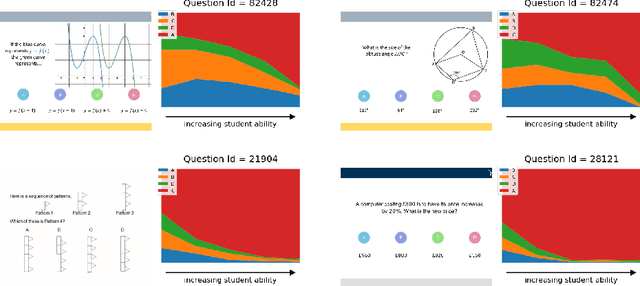
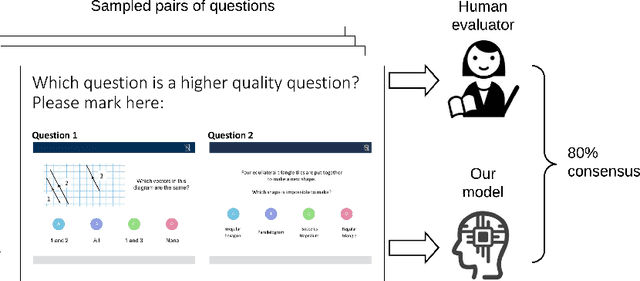
Online education platforms enable teachers to share a large number of educational resources such as questions to form exercises and quizzes for students. With large volumes of such crowd-sourced questions, quantifying the properties of these questions in crowd-sourced online education platforms is of great importance to enable both teachers and students to find high-quality and suitable resources. In this work, we propose a framework for large-scale question analysis. We utilize the state-of-the-art Bayesian deep learning method, in particular partial variational auto-encoders, to analyze real-world educational data. We also develop novel objectives to quantify question quality and difficulty. We apply our proposed framework to a real-world cohort with millions of question-answer pairs from an online education platform. Our framework not only demonstrates promising results in terms of statistical metrics but also obtains highly consistent results with domain expert evaluation.

Ergodic Measure Preserving Flows

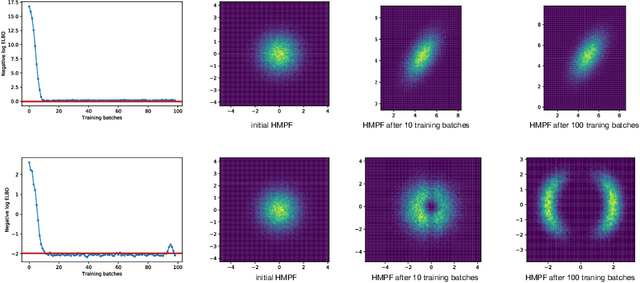
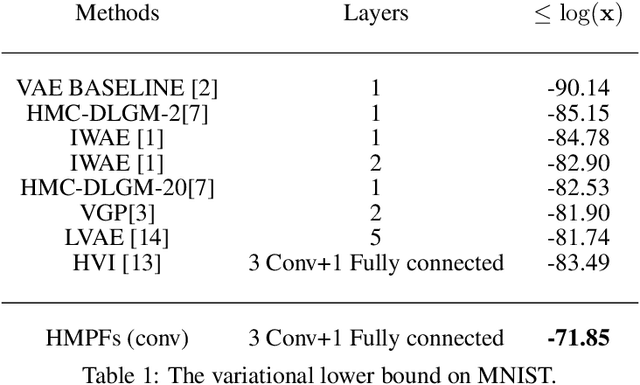
Probabilistic modelling is a general and elegant framework to capture the uncertainty, ambiguity and diversity of data. Probabilistic inference is the core technique for developing training and simulation algorithms on probabilistic models. However, the classic inference methods, like Markov chain Monte Carlo (MCMC) methods and mean-field variational inference (VI), are not computationally scalable for the recent developed probabilistic models with neural networks (NNs). This motivates many recent works on improving classic inference methods using NNs, especially, NN empowered VI. However, even with powerful NNs, VI still suffers its fundamental limitations. In this work, we propose a novel computational scalable general inference framework. With the theoretical foundation in ergodic theory, the proposed methods are not only computationally scalable like NN-based VI methods but also asymptotically accurate like MCMC. We test our method on popular benchmark problems and the results suggest that our methods can outperform NN-based VI and MCMC on deep generative models and Bayesian neural networks.

Stochastic Expectation Propagation

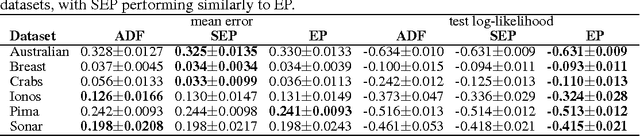
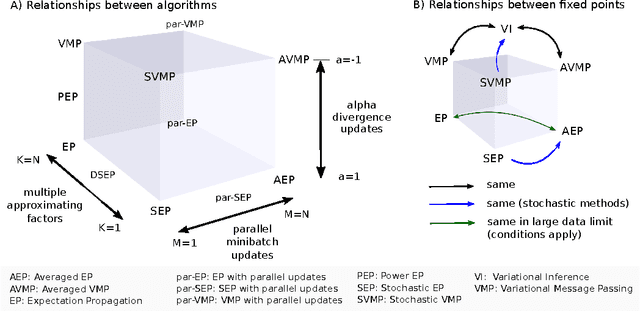
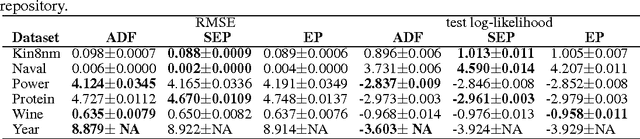
Expectation propagation (EP) is a deterministic approximation algorithm that is often used to perform approximate Bayesian parameter learning. EP approximates the full intractable posterior distribution through a set of local approximations that are iteratively refined for each datapoint. EP can offer analytic and computational advantages over other approximations, such as Variational Inference (VI), and is the method of choice for a number of models. The local nature of EP appears to make it an ideal candidate for performing Bayesian learning on large models in large-scale dataset settings. However, EP has a crucial limitation in this context: the number of approximating factors needs to increase with the number of data-points, N, which often entails a prohibitively large memory overhead. This paper presents an extension to EP, called stochastic expectation propagation (SEP), that maintains a global posterior approximation (like VI) but updates it in a local way (like EP). Experiments on a number of canonical learning problems using synthetic and real-world datasets indicate that SEP performs almost as well as full EP, but reduces the memory consumption by a factor of $N$. SEP is therefore ideally suited to performing approximate Bayesian learning in the large model, large dataset setting.