Uncertainty Modeling in Graph Neural Networks via Stochastic Differential Equations

We address the problem of learning uncertainty-aware representations for graph-structured data. While Graph Neural Ordinary Differential Equations (GNODE) are effective in learning node representations, they fail to quantify uncertainty. To address this, we introduce Latent Graph Neural Stochastic Differential Equations (LGNSDE), which enhance GNODE by embedding randomness through Brownian motion to quantify uncertainty. We provide theoretical guarantees for LGNSDE and empirically show better performance in uncertainty quantification.

Graph Classification Gaussian Processes via Spectral Features

Graph classification aims to categorise graphs based on their structure and node attributes. In this work, we propose to tackle this task using tools from graph signal processing by deriving spectral features, which we then use to design two variants of Gaussian process models for graph classification. The first variant uses spectral features based on the distribution of energy of a node feature signal over the spectrum of the graph. We show that even such a simple approach, having no learned parameters, can yield competitive performance compared to strong neural network and graph kernel baselines. A second, more sophisticated variant is designed to capture multi-scale and localised patterns in the graph by learning spectral graph wavelet filters, obtaining improved performance on synthetic and real-world data sets. Finally, we show that both models produce well calibrated uncertainty estimates, enabling reliable decision making based on the model predictions.

Transductive Kernels for Gaussian Processes on Graphs

Kernels on graphs have had limited options for node-level problems. To address this, we present a novel, generalized kernel for graphs with node feature data for semi-supervised learning. The kernel is derived from a regularization framework by treating the graph and feature data as two Hilbert spaces. We also show how numerous kernel-based models on graphs are instances of our design. A kernel defined this way has transductive properties, and this leads to improved ability to learn on fewer training points, as well as better handling of highly non-Euclidean data. We demonstrate these advantages using synthetic data where the distribution of the whole graph can inform the pattern of the labels. Finally, by utilizing a flexible polynomial of the graph Laplacian within the kernel, the model also performed effectively in semi-supervised classification on graphs of various levels of homophily.

Adaptive Gaussian Processes on Graphs via Spectral Graph Wavelets

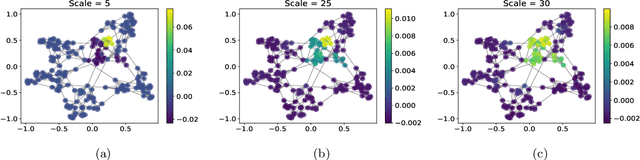
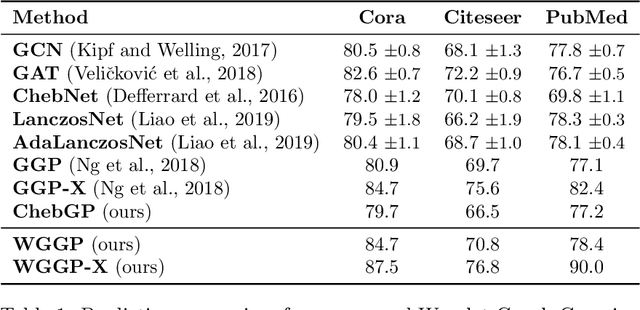
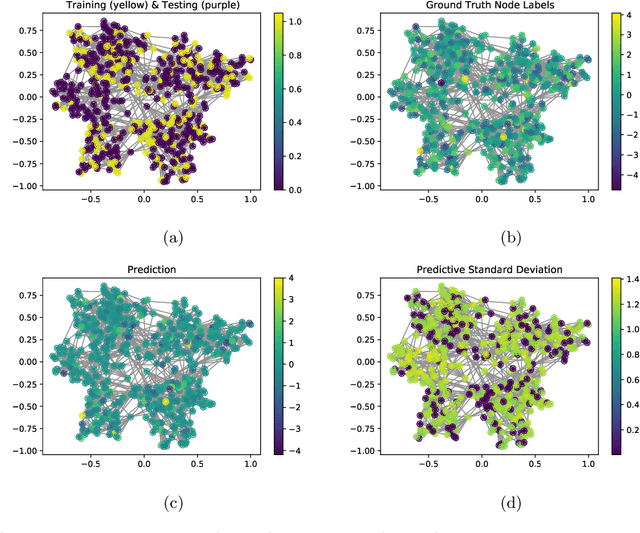
Graph-based models require aggregating information in the graph from neighbourhoods of different sizes. In particular, when the data exhibit varying levels of smoothness on the graph, a multi-scale approach is required to capture the relevant information. In this work, we propose a Gaussian process model using spectral graph wavelets, which can naturally aggregate neighbourhood information at different scales. Through maximum likelihood optimisation of the model hyperparameters, the wavelets automatically adapt to the different frequencies in the data, and as a result our model goes beyond capturing low frequency information. We achieve scalability to larger graphs by using a spectrum-adaptive polynomial approximation of the filter function, which is designed to yield a low approximation error in dense areas of the graph spectrum. Synthetic and real-world experiments demonstrate the ability of our model to infer scales accurately and produce competitive performances against state-of-the-art models in graph-based learning tasks.

Adaptive Filters and Aggregator Fusion for Efficient Graph Convolutions

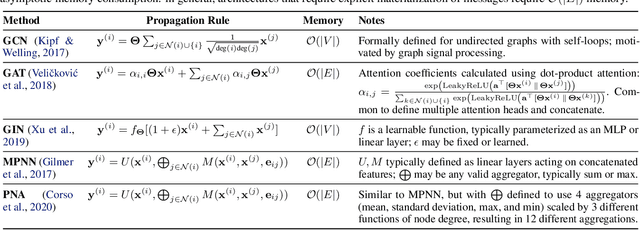
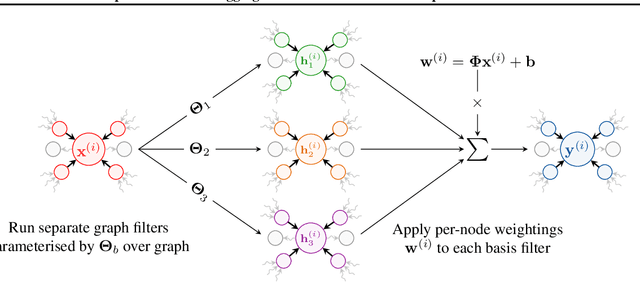
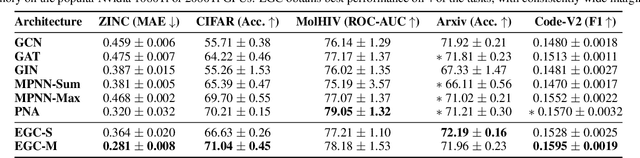
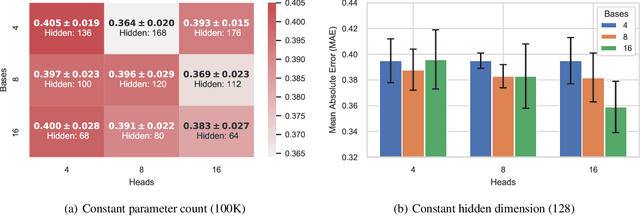
Training and deploying graph neural networks (GNNs) remains difficult due to their high memory consumption and inference latency. In this work we present a new type of GNN architecture that achieves state-of-the-art performance with lower memory consumption and latency, along with characteristics suited to accelerator implementation. Our proposal uses memory proportional to the number of vertices in the graph, in contrast to competing methods which require memory proportional to the number of edges; we find our efficient approach actually achieves higher accuracy than competing approaches across 5 large and varied datasets against strong baselines. We achieve our results by using a novel adaptive filtering approach inspired by signal processing; it can be interpreted as enabling each vertex to have its own weight matrix, and is not related to attention. Following our focus on efficient hardware usage, we propose aggregator fusion, a technique to enable GNNs to significantly boost their representational power, with only a small increase in latency of 19% over standard sparse matrix multiplication. Code and pretrained models can be found at this URL: https://github.com/shyam196/egc.

Graph Convolutional Gaussian Processes For Link Prediction

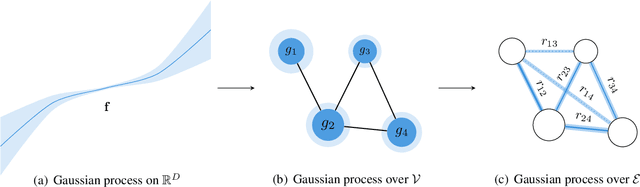
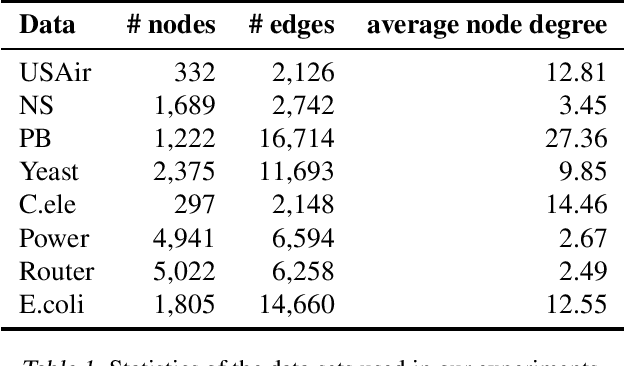
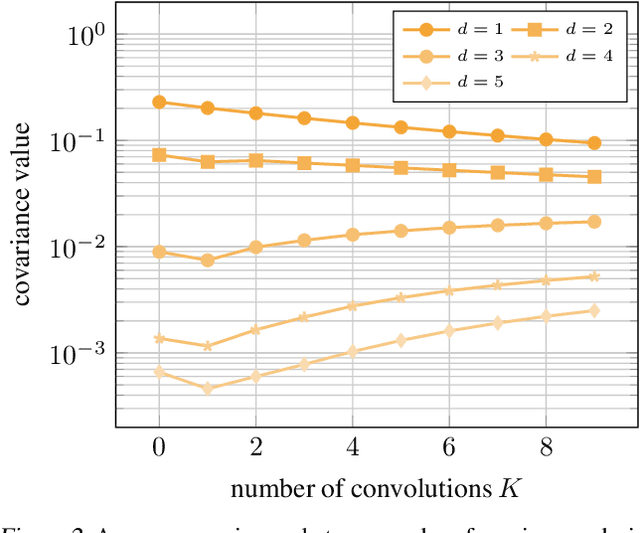
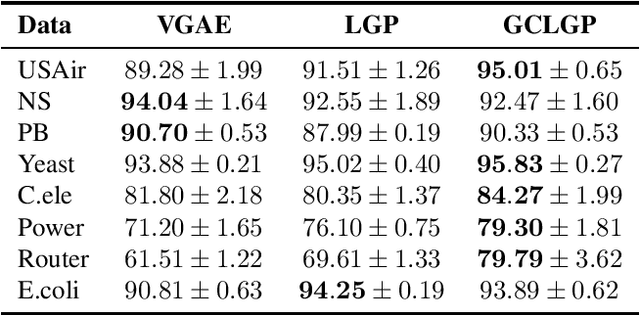
Link prediction aims to reveal missing edges in a graph. We address this task with a Gaussian process that is transformed using simplified graph convolutions to better leverage the inductive bias of the domain. To scale the Gaussian process model to large graphs, we introduce a variational inducing point method that places pseudo inputs on a graph-structured domain. We evaluate our model on eight large graphs with up to thousands of nodes and report consistent improvements over existing Gaussian process models as well as competitive performance when compared to state-of-the-art graph neural network approaches.

Spatio-Temporal Deep Graph Infomax

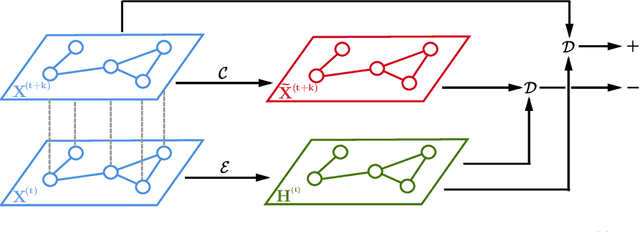
Spatio-temporal graphs such as traffic networks or gene regulatory systems present challenges for the existing deep learning methods due to the complexity of structural changes over time. To address these issues, we introduce Spatio-Temporal Deep Graph Infomax (STDGI)---a fully unsupervised node representation learning approach based on mutual information maximization that exploits both the temporal and spatial dynamics of the graph. Our model tackles the challenging task of node-level regression by training embeddings to maximize the mutual information between patches of the graph, at any given time step, and between features of the central nodes of patches, in the future. We demonstrate through experiments and qualitative studies that the learned representations can successfully encode relevant information about the input graph and improve the predictive performance of spatio-temporal auto-regressive forecasting models.