Transductive Kernels for Gaussian Processes on Graphs
Paper and Code
Nov 28, 2022
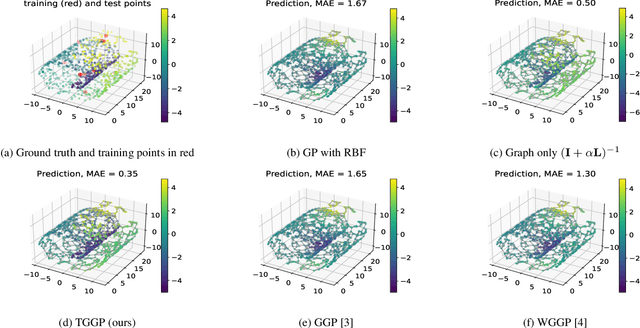
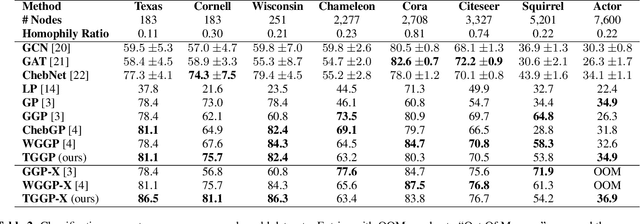
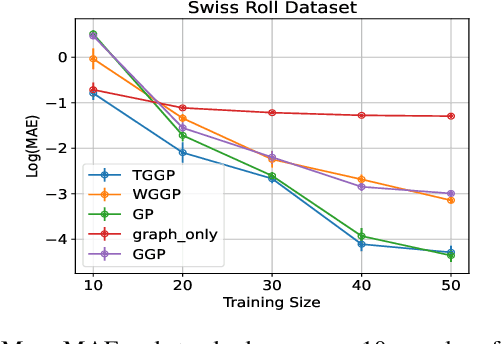
Kernels on graphs have had limited options for node-level problems. To address this, we present a novel, generalized kernel for graphs with node feature data for semi-supervised learning. The kernel is derived from a regularization framework by treating the graph and feature data as two Hilbert spaces. We also show how numerous kernel-based models on graphs are instances of our design. A kernel defined this way has transductive properties, and this leads to improved ability to learn on fewer training points, as well as better handling of highly non-Euclidean data. We demonstrate these advantages using synthetic data where the distribution of the whole graph can inform the pattern of the labels. Finally, by utilizing a flexible polynomial of the graph Laplacian within the kernel, the model also performed effectively in semi-supervised classification on graphs of various levels of homophily.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge