Graph Classification Gaussian Processes via Spectral Features

Graph classification aims to categorise graphs based on their structure and node attributes. In this work, we propose to tackle this task using tools from graph signal processing by deriving spectral features, which we then use to design two variants of Gaussian process models for graph classification. The first variant uses spectral features based on the distribution of energy of a node feature signal over the spectrum of the graph. We show that even such a simple approach, having no learned parameters, can yield competitive performance compared to strong neural network and graph kernel baselines. A second, more sophisticated variant is designed to capture multi-scale and localised patterns in the graph by learning spectral graph wavelet filters, obtaining improved performance on synthetic and real-world data sets. Finally, we show that both models produce well calibrated uncertainty estimates, enabling reliable decision making based on the model predictions.

Transductive Kernels for Gaussian Processes on Graphs

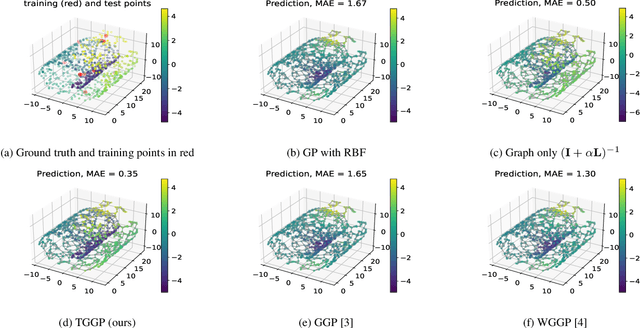
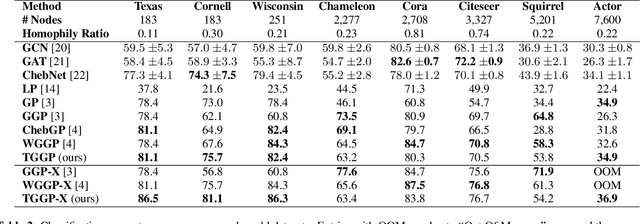
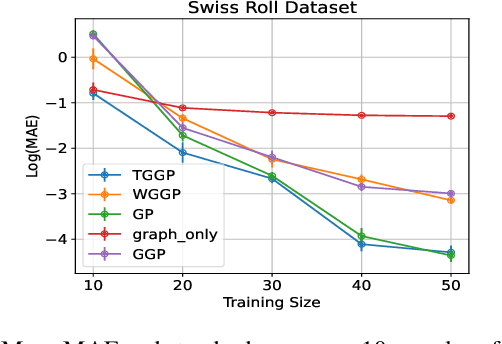
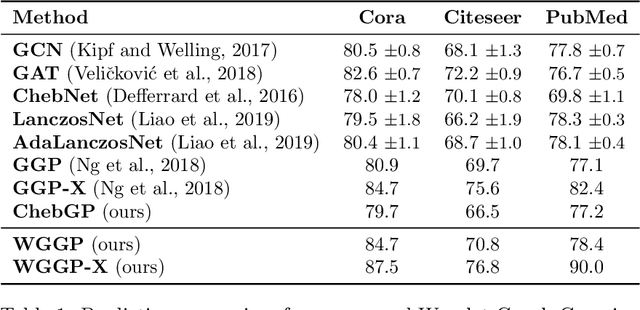
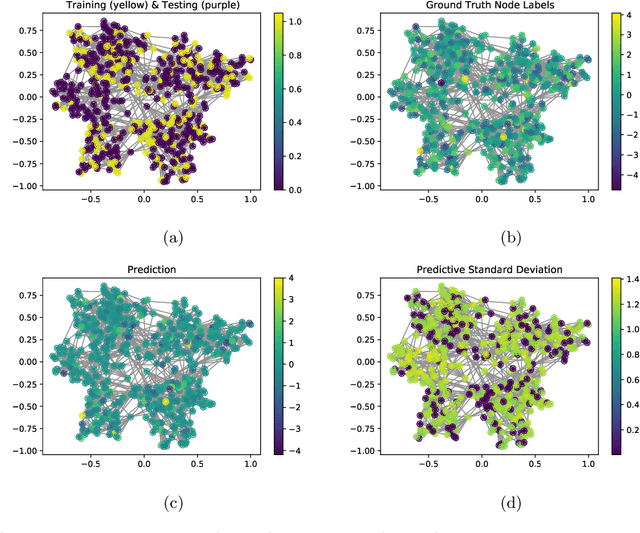
Kernels on graphs have had limited options for node-level problems. To address this, we present a novel, generalized kernel for graphs with node feature data for semi-supervised learning. The kernel is derived from a regularization framework by treating the graph and feature data as two Hilbert spaces. We also show how numerous kernel-based models on graphs are instances of our design. A kernel defined this way has transductive properties, and this leads to improved ability to learn on fewer training points, as well as better handling of highly non-Euclidean data. We demonstrate these advantages using synthetic data where the distribution of the whole graph can inform the pattern of the labels. Finally, by utilizing a flexible polynomial of the graph Laplacian within the kernel, the model also performed effectively in semi-supervised classification on graphs of various levels of homophily.

Adaptive Gaussian Processes on Graphs via Spectral Graph Wavelets

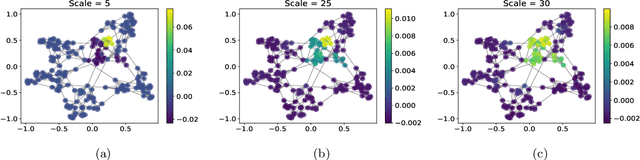
Graph-based models require aggregating information in the graph from neighbourhoods of different sizes. In particular, when the data exhibit varying levels of smoothness on the graph, a multi-scale approach is required to capture the relevant information. In this work, we propose a Gaussian process model using spectral graph wavelets, which can naturally aggregate neighbourhood information at different scales. Through maximum likelihood optimisation of the model hyperparameters, the wavelets automatically adapt to the different frequencies in the data, and as a result our model goes beyond capturing low frequency information. We achieve scalability to larger graphs by using a spectrum-adaptive polynomial approximation of the filter function, which is designed to yield a low approximation error in dense areas of the graph spectrum. Synthetic and real-world experiments demonstrate the ability of our model to infer scales accurately and produce competitive performances against state-of-the-art models in graph-based learning tasks.

Gaussian Processes on Graphs via Spectral Kernel Learning

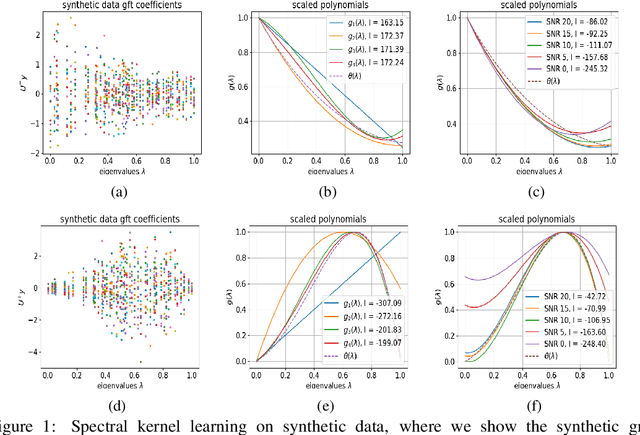
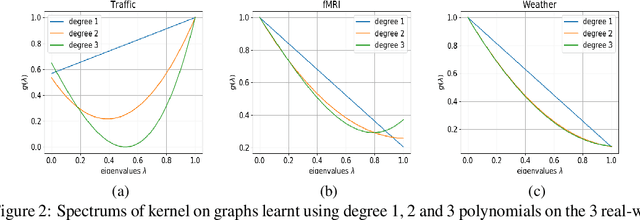
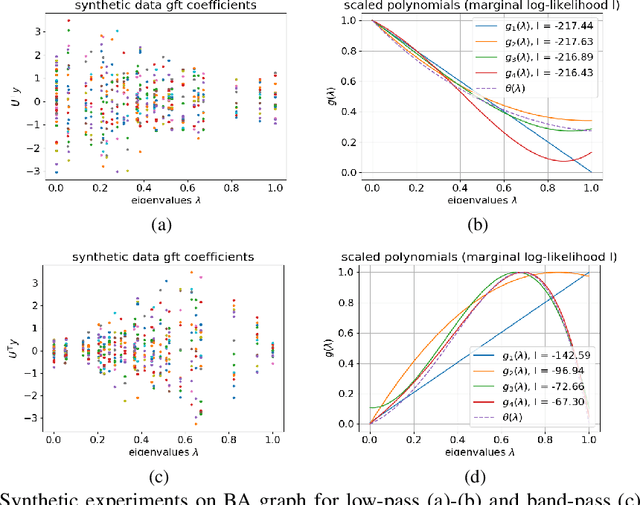
We propose a graph spectrum-based Gaussian process for prediction of signals defined on nodes of the graph. The model is designed to capture various graph signal structures through a highly adaptive kernel that incorporates a flexible polynomial function in the graph spectral domain. Unlike most existing approaches, we propose to learn such a spectral kernel, where the polynomial setup enables learning without the need for eigen-decomposition of the graph Laplacian. In addition, this kernel has the interpretability of graph filtering achieved by a bespoke maximum likelihood learning algorithm that enforces the positivity of the spectrum. We demonstrate the interpretability of the model in synthetic experiments from which we show the various ground truth spectral filters can be accurately recovered, and the adaptability translates to superior performances in the prediction of real-world graph data of various characteristics.