Ergodic Measure Preserving Flows

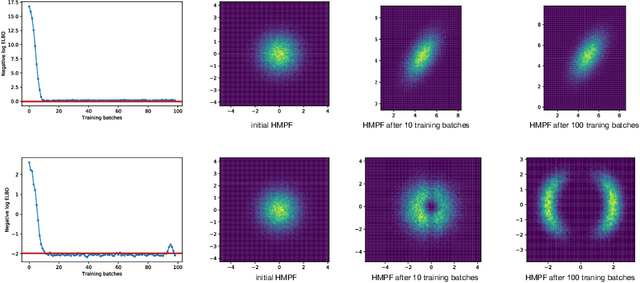
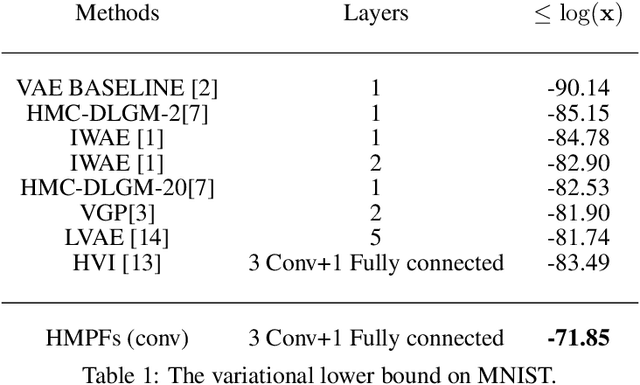
Probabilistic modelling is a general and elegant framework to capture the uncertainty, ambiguity and diversity of data. Probabilistic inference is the core technique for developing training and simulation algorithms on probabilistic models. However, the classic inference methods, like Markov chain Monte Carlo (MCMC) methods and mean-field variational inference (VI), are not computationally scalable for the recent developed probabilistic models with neural networks (NNs). This motivates many recent works on improving classic inference methods using NNs, especially, NN empowered VI. However, even with powerful NNs, VI still suffers its fundamental limitations. In this work, we propose a novel computational scalable general inference framework. With the theoretical foundation in ergodic theory, the proposed methods are not only computationally scalable like NN-based VI methods but also asymptotically accurate like MCMC. We test our method on popular benchmark problems and the results suggest that our methods can outperform NN-based VI and MCMC on deep generative models and Bayesian neural networks.