The Theory and Algorithm of Ergodic Inference

Approximate inference algorithm is one of the fundamental research fields in machine learning. The two dominant theoretical inference frameworks in machine learning are variational inference (VI) and Markov chain Monte Carlo (MCMC). However, because of the fundamental limitation in the theory, it is very challenging to improve existing VI and MCMC methods on both the computational scalability and statistical efficiency. To overcome this obstacle, we propose a new theoretical inference framework called ergodic Inference based on the fundamental property of ergodic transformations. The key contribution of this work is to establish the theoretical foundation of ergodic inference for the development of practical algorithms in future work.

Ergodic Measure Preserving Flows

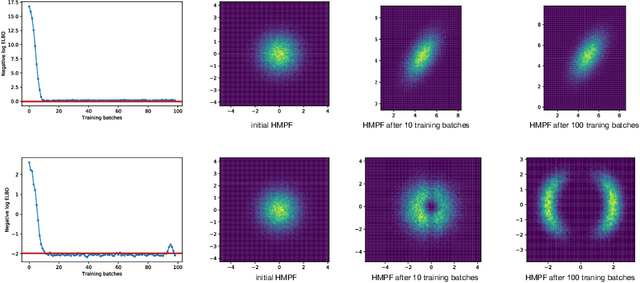
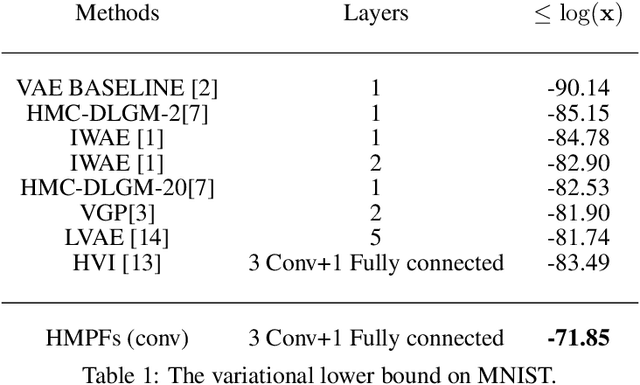
Probabilistic modelling is a general and elegant framework to capture the uncertainty, ambiguity and diversity of data. Probabilistic inference is the core technique for developing training and simulation algorithms on probabilistic models. However, the classic inference methods, like Markov chain Monte Carlo (MCMC) methods and mean-field variational inference (VI), are not computationally scalable for the recent developed probabilistic models with neural networks (NNs). This motivates many recent works on improving classic inference methods using NNs, especially, NN empowered VI. However, even with powerful NNs, VI still suffers its fundamental limitations. In this work, we propose a novel computational scalable general inference framework. With the theoretical foundation in ergodic theory, the proposed methods are not only computationally scalable like NN-based VI methods but also asymptotically accurate like MCMC. We test our method on popular benchmark problems and the results suggest that our methods can outperform NN-based VI and MCMC on deep generative models and Bayesian neural networks.

Semi-Separable Hamiltonian Monte Carlo for Inference in Bayesian Hierarchical Models

Sampling from hierarchical Bayesian models is often difficult for MCMC methods, because of the strong correlations between the model parameters and the hyperparameters. Recent Riemannian manifold Hamiltonian Monte Carlo (RMHMC) methods have significant potential advantages in this setting, but are computationally expensive. We introduce a new RMHMC method, which we call semi-separable Hamiltonian Monte Carlo, which uses a specially designed mass matrix that allows the joint Hamiltonian over model parameters and hyperparameters to decompose into two simpler Hamiltonians. This structure is exploited by a new integrator which we call the alternating blockwise leapfrog algorithm. The resulting method can mix faster than simpler Gibbs sampling while being simpler and more efficient than previous instances of RMHMC.