Graph Neural Stochastic Differential Equations

We present a novel model Graph Neural Stochastic Differential Equations (Graph Neural SDEs). This technique enhances the Graph Neural Ordinary Differential Equations (Graph Neural ODEs) by embedding randomness into data representation using Brownian motion. This inclusion allows for the assessment of prediction uncertainty, a crucial aspect frequently missed in current models. In our framework, we spotlight the \textit{Latent Graph Neural SDE} variant, demonstrating its effectiveness. Through empirical studies, we find that Latent Graph Neural SDEs surpass conventional models like Graph Convolutional Networks and Graph Neural ODEs, especially in confidence prediction, making them superior in handling out-of-distribution detection across both static and spatio-temporal contexts.

Approximate Latent Force Model Inference

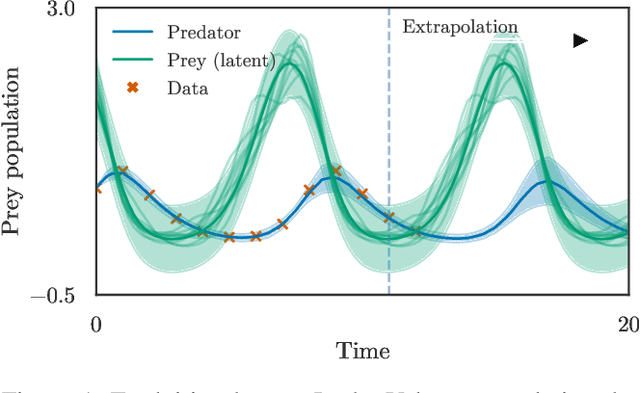
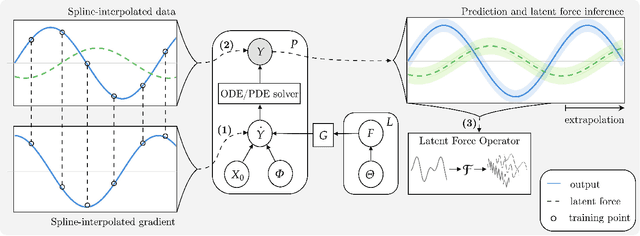
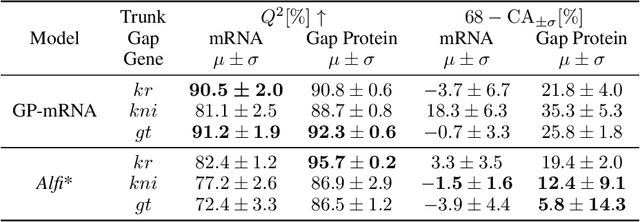
Physically-inspired latent force models offer an interpretable alternative to purely data driven tools for inference in dynamical systems. They carry the structure of differential equations and the flexibility of Gaussian processes, yielding interpretable parameters and dynamics-imposed latent functions. However, the existing inference techniques associated with these models rely on the exact computation of posterior kernel terms which are seldom available in analytical form. Most applications relevant to practitioners, such as Hill equations or diffusion equations, are hence intractable. In this paper, we overcome these computational problems by proposing a variational solution to a general class of non-linear and parabolic partial differential equation latent force models. Further, we show that a neural operator approach can scale our model to thousands of instances, enabling fast, distributed computation. We demonstrate the efficacy and flexibility of our framework by achieving competitive performance on several tasks where the kernels are of varying degrees of tractability.