DFF: Decision-Focused Fine-tuning for Smarter Predict-then-Optimize with Limited Data

Decision-focused learning (DFL) offers an end-to-end approach to the predict-then-optimize (PO) framework by training predictive models directly on decision loss (DL), enhancing decision-making performance within PO contexts. However, the implementation of DFL poses distinct challenges. Primarily, DL can result in deviation from the physical significance of the predictions under limited data. Additionally, some predictive models are non-differentiable or black-box, which cannot be adjusted using gradient-based methods. To tackle the above challenges, we propose a novel framework, Decision-Focused Fine-tuning (DFF), which embeds the DFL module into the PO pipeline via a novel bias correction module. DFF is formulated as a constrained optimization problem that maintains the proximity of the DL-enhanced model to the original predictive model within a defined trust region. We theoretically prove that DFF strictly confines prediction bias within a predetermined upper bound, even with limited datasets, thereby substantially reducing prediction shifts caused by DL under limited data. Furthermore, the bias correction module can be integrated into diverse predictive models, enhancing adaptability to a broad range of PO tasks. Extensive evaluations on synthetic and real-world datasets, including network flow, portfolio optimization, and resource allocation problems with different predictive models, demonstrate that DFF not only improves decision performance but also adheres to fine-tuning constraints, showcasing robust adaptability across various scenarios.

Navigating Data Corruption in Machine Learning: Balancing Quality, Quantity, and Imputation Strategies

Data corruption, including missing and noisy data, poses significant challenges in real-world machine learning. This study investigates the effects of data corruption on model performance and explores strategies to mitigate these effects through two experimental setups: supervised learning with NLP tasks (NLP-SL) and deep reinforcement learning for traffic signal optimization (Signal-RL). We analyze the relationship between data corruption levels and model performance, evaluate the effectiveness of data imputation methods, and assess the utility of enlarging datasets to address data corruption. Our results show that model performance under data corruption follows a diminishing return curve, modeled by the exponential function. Missing data, while detrimental, is less harmful than noisy data, which causes severe performance degradation and training instability, particularly in sequential decision-making tasks like Signal-RL. Imputation strategies involve a trade-off: they recover missing information but may introduce noise. Their effectiveness depends on imputation accuracy and corruption ratio. We identify distinct regions in the imputation advantage heatmap, including an "imputation advantageous corner" and an "imputation disadvantageous edge" and classify tasks as "noise-sensitive" or "noise-insensitive" based on their decision boundaries. Furthermore, we find that increasing dataset size mitigates but cannot fully overcome the effects of data corruption. The marginal utility of additional data diminishes as corruption increases. An empirical rule emerges: approximately 30% of the data is critical for determining performance, while the remaining 70% has minimal impact. These findings provide actionable insights into data preprocessing, imputation strategies, and data collection practices, guiding the development of robust machine learning systems in noisy environments.

The Epochal Sawtooth Effect: Unveiling Training Loss Oscillations in Adam and Other Optimizers

In this paper, we identify and analyze a recurring training loss pattern, which we term the \textit{Epochal Sawtooth Effect (ESE)}, commonly observed during training with adaptive gradient-based optimizers, particularly Adam optimizer. This pattern is characterized by a sharp drop in loss at the beginning of each epoch, followed by a gradual increase, resulting in a sawtooth-shaped loss curve. Through empirical observations, we demonstrate that while this effect is most pronounced with Adam, it persists, although less severely, with other optimizers such as RMSProp. We provide an in-depth explanation of the underlying mechanisms that lead to the Epochal Sawtooth Effect. The influences of factors like \(\beta\), batch size, data shuffling on this pattern have been studied. We quantify the influence of \(\beta_2\) on the shape of the loss curve, showing that higher values of \(\beta_2\) result in a nearly linear increase in loss, while lower values create a concave upward trend. Our analysis reveals that this behavior stems from the adaptive learning rate controlled by the second moment estimate, with \(\beta_1\) playing a minimal role when \(\beta_2\) is large. To support our analysis, we replicate this phenomenon through a controlled quadratic minimization task. By incrementally solving a series of quadratic optimization problems using Adam, we demonstrate that the Epochal Sawtooth Effect can emerge even in simple optimization scenarios, reinforcing the generality of this pattern. This paper provides both theoretical insights and quantitative analysis, offering a comprehensive understanding of this ubiquitous phenomenon in modern optimization techniques.

Vehicle-group-based Crash Risk Formation and Propagation Analysis for Expressways

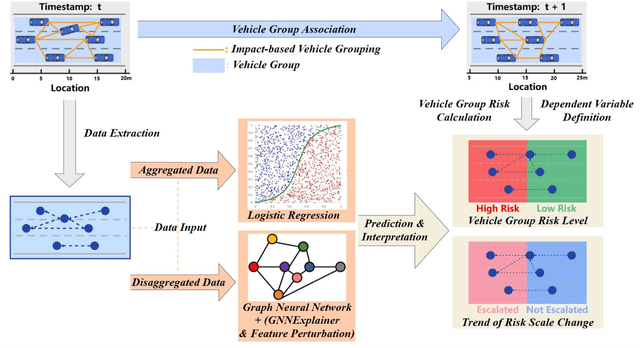
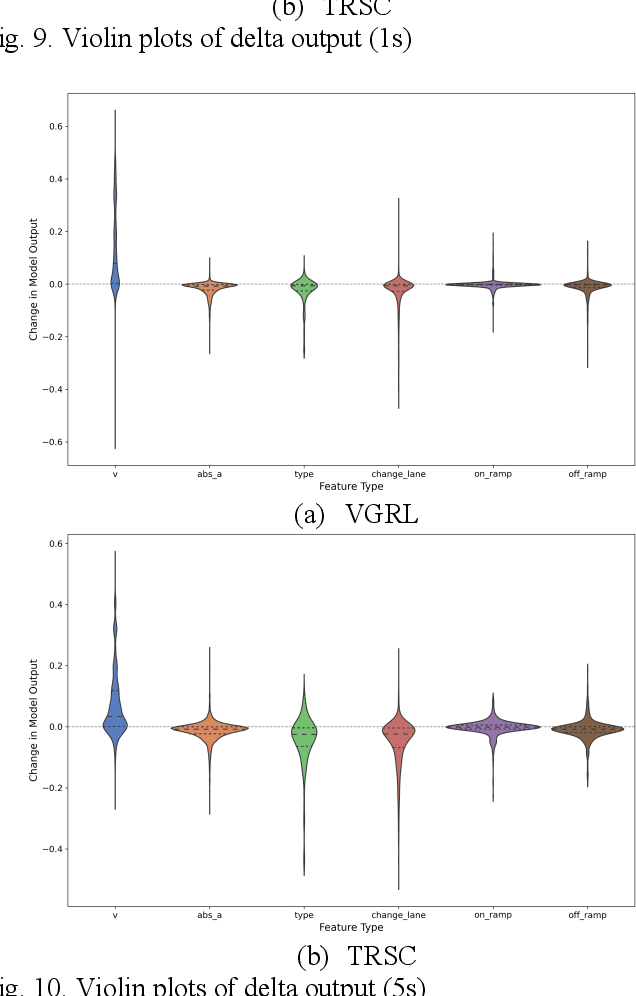
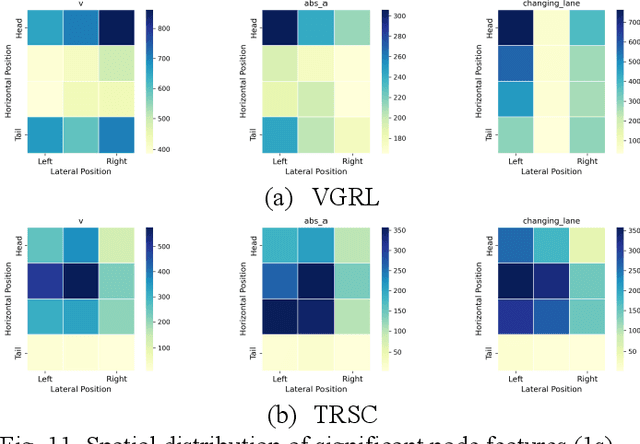
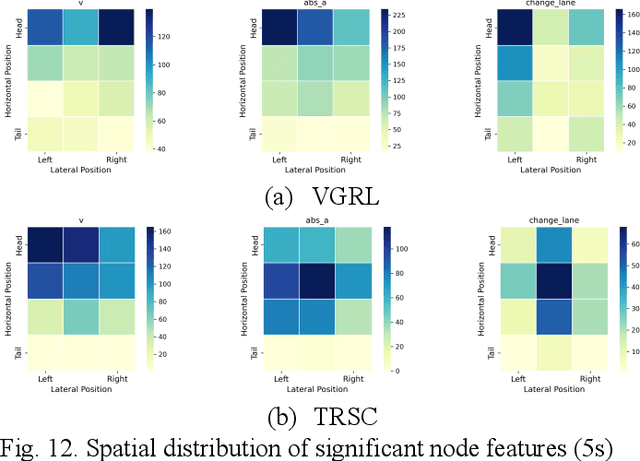
Previous studies in predicting crash risk primarily associated the number or likelihood of crashes on a road segment with traffic parameters or geometric characteristics of the segment, usually neglecting the impact of vehicles' continuous movement and interactions with nearby vehicles. Advancements in communication technologies have empowered driving information collected from surrounding vehicles, enabling the study of group-based crash risks. Based on high-resolution vehicle trajectory data, this research focused on vehicle groups as the subject of analysis and explored risk formation and propagation mechanisms considering features of vehicle groups and road segments. Several key factors contributing to crash risks were identified, including past high-risk vehicle-group states, complex vehicle behaviors, high percentage of large vehicles, frequent lane changes within a vehicle group, and specific road geometries. A multinomial logistic regression model was developed to analyze the spatial risk propagation patterns, which were classified based on the trend of high-risk occurrences within vehicle groups. The results indicated that extended periods of high-risk states, increase in vehicle-group size, and frequent lane changes are associated with adverse risk propagation patterns. Conversely, smoother traffic flow and high initial crash risk values are linked to risk dissipation. Furthermore, the study conducted sensitivity analysis on different types of classifiers, prediction time intervalsss and adaptive TTC thresholds. The highest AUC value for vehicle-group risk prediction surpassed 0.93. The findings provide valuable insights to researchers and practitioners in understanding and prediction of vehicle-group safety, ultimately improving active traffic safety management and operations of Connected and Autonomous Vehicles.