Learning Dynamic Representations and Policies from Multimodal Clinical Time-Series with Informative Missingness

Multimodal clinical records contain structured measurements and clinical notes recorded over time, offering rich temporal information about the evolution of patient health. Yet these observations are sparse, and whether they are recorded depends on the patient's latent condition. Observation patterns also differ across modalities, as structured measurements and clinical notes arise under distinct recording processes. While prior work has developed methods that accommodate missingness in clinical time series, how to extract and use the information carried by the observation process itself remains underexplored. We therefore propose a patient representation learning framework for multimodal clinical time series that explicitly leverages informative missingness. The framework combines (1) a multimodal encoder that captures signals from structured and textual data together with their observation patterns, (2) a Bayesian filtering module that updates a latent patient state over time from observed multimodal signals, and (3) downstream modules for offline treatment policy learning and patient outcome prediction based on the learned patient state. We evaluate the framework on ICU sepsis cohorts from MIMIC-III, MIMIC-IV, and eICU. It improves both offline treatment policy learning and adverse outcome prediction, achieving FQE 0.679 versus 0.528 for clinician behavior and AUROC 0.886 for post-72-hour mortality prediction on MIMIC-III.

Partial Identification under Missing Data Using Weak Shadow Variables from Pretrained Models

Estimating population quantities such as mean outcomes from user feedback is fundamental to platform evaluation and social science, yet feedback is often missing not at random (MNAR): users with stronger opinions are more likely to respond, so standard estimators are biased and the estimand is not identified without additional assumptions. Existing approaches typically rely on strong parametric assumptions or bespoke auxiliary variables that may be unavailable in practice. In this paper, we develop a partial identification framework in which sharp bounds on the estimand are obtained by solving a pair of linear programs whose constraints encode the observed data structure. This formulation naturally incorporates outcome predictions from pretrained models, including large language models (LLMs), as additional linear constraints that tighten the feasible set. We call these predictions weak shadow variables: they satisfy a conditional independence assumption with respect to missingness but need not meet the completeness conditions required by classical shadow-variable methods. When predictions are sufficiently informative, the bounds collapse to a point, recovering standard identification as a special case. In finite samples, to provide valid coverage of the identified set, we propose a set-expansion estimator that achieves slower-than-$\sqrt{n}$ convergence rate in the set-identified regime and the standard $\sqrt{n}$ rate under point identification. In simulations and semi-synthetic experiments on customer-service dialogues, we find that LLM predictions are often ill-conditioned for classical shadow-variable methods yet remain highly effective in our framework. They shrink identification intervals by 75--83\% while maintaining valid coverage under realistic MNAR mechanisms.

Sequential Treatment Effect Estimation with Unmeasured Confounders

This paper studies the cumulative causal effects of sequential treatments in the presence of unmeasured confounders. It is a critical issue in sequential decision-making scenarios where treatment decisions and outcomes dynamically evolve over time. Advanced causal methods apply transformer as a backbone to model such time sequences, which shows superiority in capturing long time dependence and periodic patterns via attention mechanism. However, even they control the observed confounding, these estimators still suffer from unmeasured confounders, which influence both treatment assignments and outcomes. How to adjust the latent confounding bias in sequential treatment effect estimation remains an open challenge. Therefore, we propose a novel Decomposing Sequential Instrumental Variable framework for CounterFactual Regression (DSIV-CFR), relying on a common negative control assumption. Specifically, an instrumental variable (IV) is a special negative control exposure, while the previous outcome serves as a negative control outcome. This allows us to recover the IVs latent in observation variables and estimate sequential treatment effects via a generalized moment condition. We conducted experiments on 4 datasets and achieved significant performance in one- and multi-step prediction, supported by which we can identify optimal treatments for dynamic systems.

Can We Validate Counterfactual Estimations in the Presence of General Network Interference?

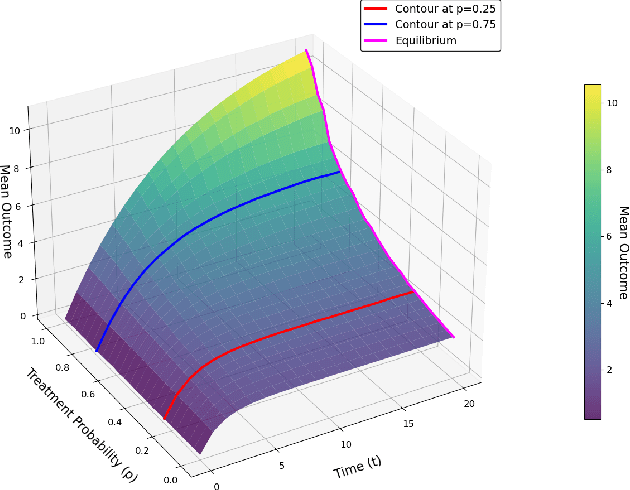
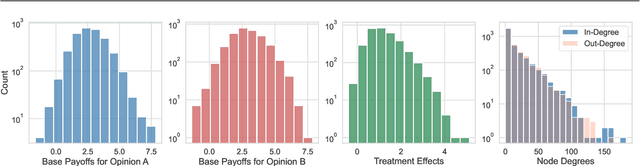
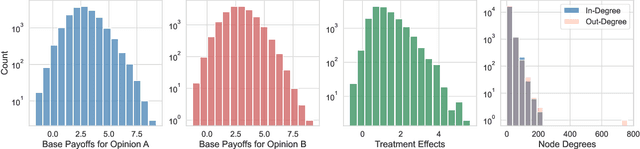
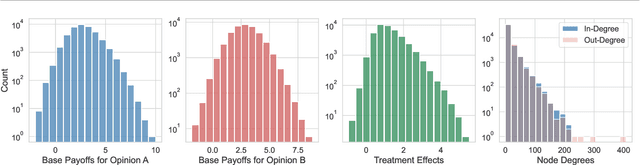
In experimental settings with network interference, a unit's treatment can influence outcomes of other units, challenging both causal effect estimation and its validation. Classic validation approaches fail as outcomes are only observable under one treatment scenario and exhibit complex correlation patterns due to interference. To address these challenges, we introduce a new framework enabling cross-validation for counterfactual estimation. At its core is our distribution-preserving network bootstrap method -- a theoretically-grounded approach inspired by approximate message passing. This method creates multiple subpopulations while preserving the underlying distribution of network effects. We extend recent causal message-passing developments by incorporating heterogeneous unit-level characteristics and varying local interactions, ensuring reliable finite-sample performance through non-asymptotic analysis. We also develop and publicly release a comprehensive benchmark toolbox with diverse experimental environments, from networks of interacting AI agents to opinion formation in real-world communities and ride-sharing applications. These environments provide known ground truth values while maintaining realistic complexities, enabling systematic examination of causal inference methods. Extensive evaluation across these environments demonstrates our method's robustness to diverse forms of network interference. Our work provides researchers with both a practical estimation framework and a standardized platform for testing future methodological developments.

Higher-Order Causal Message Passing for Experimentation with Complex Interference

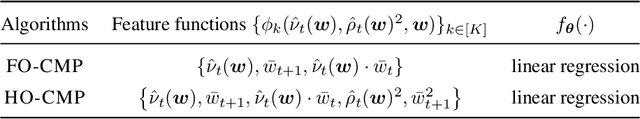
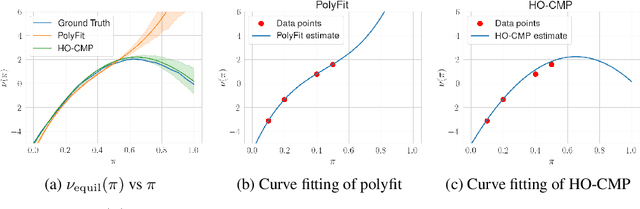
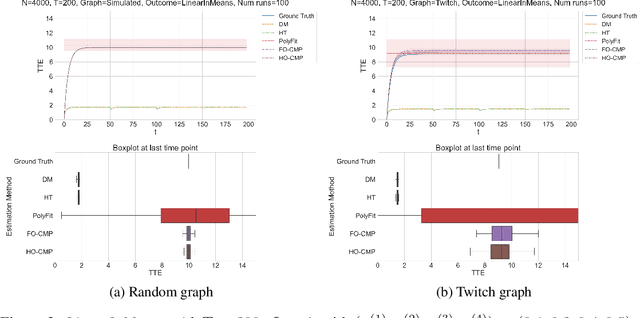
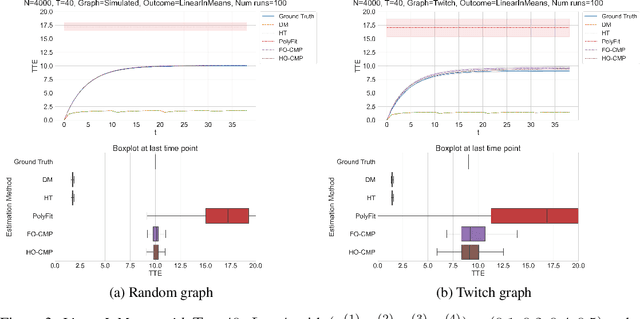
Accurate estimation of treatment effects is essential for decision-making across various scientific fields. This task, however, becomes challenging in areas like social sciences and online marketplaces, where treating one experimental unit can influence outcomes for others through direct or indirect interactions. Such interference can lead to biased treatment effect estimates, particularly when the structure of these interactions is unknown. We address this challenge by introducing a new class of estimators based on causal message-passing, specifically designed for settings with pervasive, unknown interference. Our estimator draws on information from the sample mean and variance of unit outcomes and treatments over time, enabling efficient use of observed data to estimate the evolution of the system state. Concretely, we construct non-linear features from the moments of unit outcomes and treatments and then learn a function that maps these features to future mean and variance of unit outcomes. This allows for the estimation of the treatment effect over time. Extensive simulations across multiple domains, using synthetic and real network data, demonstrate the efficacy of our approach in estimating total treatment effect dynamics, even in cases where interference exhibits non-monotonic behavior in the probability of treatment.

Generalized Encouragement-Based Instrumental Variables for Counterfactual Regression

In causal inference, encouragement designs (EDs) are widely used to analyze causal effects, when randomized controlled trials (RCTs) are impractical or compliance to treatment cannot be perfectly enforced. Unlike RCTs, which directly allocate treatments, EDs randomly assign encouragement policies that positively motivate individuals to engage in a specific treatment. These random encouragements act as instrumental variables (IVs), facilitating the identification of causal effects through leveraging exogenous perturbations in discrete treatment scenarios. However, real-world applications of encouragement designs often face challenges such as incomplete randomization, limited experimental data, and significantly fewer encouragements compared to treatments, hindering precise causal effect estimation. To address this, this paper introduces novel theories and algorithms for identifying the Conditional Average Treatment Effect (CATE) using variations in encouragement. Further, by leveraging both observational and encouragement data, we propose a generalized IV estimator, named Encouragement-based Counterfactual Regression (EnCounteR), to effectively estimate the causal effects. Extensive experiments on both synthetic and real-world datasets demonstrate the superiority of EnCounteR over existing methods.

Causal Inference with Complex Treatments: A Survey

Causal inference plays an important role in explanatory analysis and decision making across various fields like statistics, marketing, health care, and education. Its main task is to estimate treatment effects and make intervention policies. Traditionally, most of the previous works typically focus on the binary treatment setting that there is only one treatment for a unit to adopt or not. However, in practice, the treatment can be much more complex, encompassing multi-valued, continuous, or bundle options. In this paper, we refer to these as complex treatments and systematically and comprehensively review the causal inference methods for addressing them. First, we formally revisit the problem definition, the basic assumptions, and their possible variations under specific conditions. Second, we sequentially review the related methods for multi-valued, continuous, and bundled treatment settings. In each situation, we tentatively divide the methods into two categories: those conforming to the unconfoundedness assumption and those violating it. Subsequently, we discuss the available datasets and open-source codes. Finally, we provide a brief summary of these works and suggest potential directions for future research.

Data-Driven Switchback Experiments: Theoretical Tradeoffs and Empirical Bayes Designs

We study the design and analysis of switchback experiments conducted on a single aggregate unit. The design problem is to partition the continuous time space into intervals and switch treatments between intervals, in order to minimize the estimation error of the treatment effect. We show that the estimation error depends on four factors: carryover effects, periodicity, serially correlated outcomes, and impacts from simultaneous experiments. We derive a rigorous bias-variance decomposition and show the tradeoffs of the estimation error from these factors. The decomposition provides three new insights in choosing a design: First, balancing the periodicity between treated and control intervals reduces the variance; second, switching less frequently reduces the bias from carryover effects while increasing the variance from correlated outcomes, and vice versa; third, randomizing interval start and end points reduces both bias and variance from simultaneous experiments. Combining these insights, we propose a new empirical Bayes design approach. This approach uses prior data and experiments for designing future experiments. We illustrate this approach using real data from a ride-sharing platform, yielding a design that reduces MSE by 33% compared to the status quo design used on the platform.

Contrastive Balancing Representation Learning for Heterogeneous Dose-Response Curves Estimation

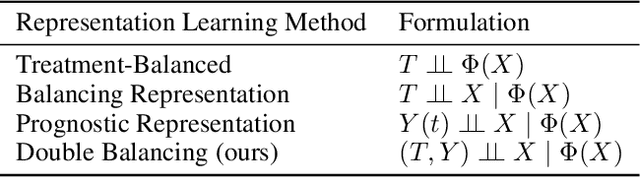
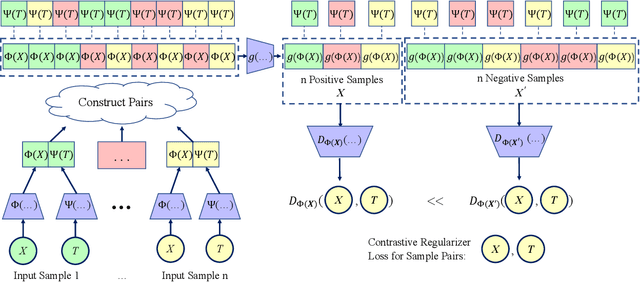
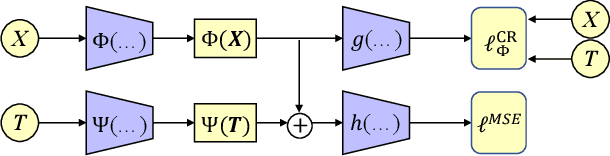
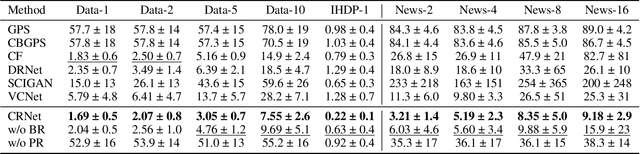
Estimating the individuals' potential response to varying treatment doses is crucial for decision-making in areas such as precision medicine and management science. Most recent studies predict counterfactual outcomes by learning a covariate representation that is independent of the treatment variable. However, such independence constraints neglect much of the covariate information that is useful for counterfactual prediction, especially when the treatment variables are continuous. To tackle the above issue, in this paper, we first theoretically demonstrate the importance of the balancing and prognostic representations for unbiased estimation of the heterogeneous dose-response curves, that is, the learned representations are constrained to satisfy the conditional independence between the covariates and both of the treatment variables and the potential responses. Based on this, we propose a novel Contrastive balancing Representation learning Network using a partial distance measure, called CRNet, for estimating the heterogeneous dose-response curves without losing the continuity of treatments. Extensive experiments are conducted on synthetic and real-world datasets demonstrating that our proposal significantly outperforms previous methods.

Pareto-Optimal Estimation and Policy Learning on Short-term and Long-term Treatment Effects

This paper focuses on developing Pareto-optimal estimation and policy learning to identify the most effective treatment that maximizes the total reward from both short-term and long-term effects, which might conflict with each other. For example, a higher dosage of medication might increase the speed of a patient's recovery (short-term) but could also result in severe long-term side effects. Although recent works have investigated the problems about short-term or long-term effects or the both, how to trade-off between them to achieve optimal treatment remains an open challenge. Moreover, when multiple objectives are directly estimated using conventional causal representation learning, the optimization directions among various tasks can conflict as well. In this paper, we systematically investigate these issues and introduce a Pareto-Efficient algorithm, comprising Pareto-Optimal Estimation (POE) and Pareto-Optimal Policy Learning (POPL), to tackle them. POE incorporates a continuous Pareto module with representation balancing, enhancing estimation efficiency across multiple tasks. As for POPL, it involves deriving short-term and long-term outcomes linked with various treatment levels, facilitating an exploration of the Pareto frontier emanating from these outcomes. Results on both the synthetic and real-world datasets demonstrate the superiority of our method.