Scalably Enhancing the Clinical Validity of a Task Benchmark with Physician Oversight

Automating the calculation of clinical risk scores offers a significant opportunity to reduce physician administrative burden and enhance patient care. The current standard for evaluating this capability is MedCalc-Bench, a large-scale dataset constructed using LLM-based feature extraction and rule-based aggregation. However, treating such model-generated benchmarks as static oracles risks enshrining historical model errors as evaluation gold standards, a problem dangerously amplified when these datasets serve as reward signals for Reinforcement Learning (RL). In this work, we propose viewing benchmarks for complex tasks such as clinical score computation as ''in-progress living documents'' that should be periodically re-evaluated as the processes for creating them improve. We introduce a systematic, physician-in-the-loop pipeline that leverages advanced agentic verifiers to audit and relabel MedCalc-Bench, utilizing automated triage to reserve scarce clinician attention for the most contentious instances. Our audit reveals that a notable fraction of original labels diverge from medical ground truth due to extraction errors, calculator logic mismatches, and clinical ambiguity. To study whether this label noise meaningfully impacts downstream RL training, we fine-tune a Qwen3-8B model via Group Relative Policy Optimization (GRPO) and demonstrate that training on corrected labels yields an 8.7% absolute improvement in accuracy over the original baseline -- validating that label noise materially affects model evaluation. These findings underscore that in safety-critical domains, rigorous benchmark maintenance is a prerequisite for genuine model alignment.

Estimating Total Effects in Bipartite Experiments with Spillovers and Partial Eligibility

We study randomized experiments in bipartite systems where only a subset of treatment-side units are eligible for assignment while all units continue to interact, generating interference. We formalize eligibility-constrained bipartite experiments and define estimands aligned with full deployment: the Primary Total Treatment Effect (PTTE) on eligible units and the Secondary Total Treatment Effect (STTE) on ineligible units. Under randomization within the eligible set, we give identification conditions and develop interference-aware ensemble estimators that combine exposure mappings, generalized propensity scores, and flexible machine learning. We further introduce a projection that links treatment- and outcome-level estimands; this mapping is exact under a Linear Additive Edges condition and enables estimation on the (typically much smaller) treatment side with deterministic aggregation to outcomes. In simulations with known ground truth across realistic exposure regimes, the proposed estimators recover PTTE and STTE with low bias and variance and reduce the bias that could arise when interference is ignored. Two field experiments illustrate practical relevance: our method corrects the direction of expected interference bias for a pre-specified metric in both studies and reverses the sign and significance of the primary decision metric in one case.

Simulating and Experimenting with Social Media Mobilization Using LLM Agents

Online social networks have transformed the ways in which political mobilization messages are disseminated, raising new questions about how peer influence operates at scale. Building on the landmark 61-million-person Facebook experiment \citep{bond201261}, we develop an agent-based simulation framework that integrates real U.S. Census demographic distributions, authentic Twitter network topology, and heterogeneous large language model (LLM) agents to examine the effect of mobilization messages on voter turnout. Each simulated agent is assigned demographic attributes, a personal political stance, and an LLM variant (\texttt{GPT-4.1}, \texttt{GPT-4.1-Mini}, or \texttt{GPT-4.1-Nano}) reflecting its political sophistication. Agents interact over realistic social network structures, receiving personalized feeds and dynamically updating their engagement behaviors and voting intentions. Experimental conditions replicate the informational and social mobilization treatments of the original Facebook study. Across scenarios, the simulator reproduces qualitative patterns observed in field experiments, including stronger mobilization effects under social message treatments and measurable peer spillovers. Our framework provides a controlled, reproducible environment for testing counterfactual designs and sensitivity analyses in political mobilization research, offering a bridge between high-validity field experiments and flexible computational modeling.\footnote{Code and data available at https://github.com/CausalMP/LLM-SocioPol}

The Oversight Game: Learning to Cooperatively Balance an AI Agent's Safety and Autonomy

As increasingly capable agents are deployed, a central safety question is how to retain meaningful human control without modifying the underlying system. We study a minimal control interface where an agent chooses whether to act autonomously (play) or defer (ask), while a human simultaneously chooses whether to be permissive (trust) or to engage in oversight (oversee). If the agent defers, the human's choice determines the outcome, potentially leading to a corrective action or a system shutdown. We model this interaction as a two-player Markov Game. Our analysis focuses on cases where this game qualifies as a Markov Potential Game (MPG), a class of games where we can provide an alignment guarantee: under a structural assumption on the human's value function, any decision by the agent to act more autonomously that benefits itself cannot harm the human's value. We also analyze extensions to this MPG framework. Theoretically, this perspective provides conditions for a specific form of intrinsic alignment. If the reward structures of the human-agent game meet these conditions, we have a formal guarantee that the agent improving its own outcome will not harm the human's. Practically, this model motivates a transparent control layer with predictable incentives where the agent learns to defer when risky and act when safe, while its pretrained policy and the environment's reward structure remain untouched. Our gridworld simulation shows that through independent learning, the agent and human discover their optimal oversight roles. The agent learns to ask when uncertain and the human learns when to oversee, leading to an emergent collaboration that avoids safety violations introduced post-training. This demonstrates a practical method for making misaligned models safer after deployment.

On Aligning Prediction Models with Clinical Experiential Learning: A Prostate Cancer Case Study

Over the past decade, the use of machine learning (ML) models in healthcare applications has rapidly increased. Despite high performance, modern ML models do not always capture patterns the end user requires. For example, a model may predict a non-monotonically decreasing relationship between cancer stage and survival, keeping all other features fixed. In this paper, we present a reproducible framework for investigating this misalignment between model behavior and clinical experiential learning, focusing on the effects of underspecification of modern ML pipelines. In a prostate cancer outcome prediction case study, we first identify and address these inconsistencies by incorporating clinical knowledge, collected by a survey, via constraints into the ML model, and subsequently analyze the impact on model performance and behavior across degrees of underspecification. The approach shows that aligning the ML model with clinical experiential learning is possible without compromising performance. Motivated by recent literature in generative AI, we further examine the feasibility of a feedback-driven alignment approach in non-generative AI clinical risk prediction models through a randomized experiment with clinicians. Our findings illustrate that, by eliciting clinicians' model preferences using our proposed methodology, the larger the difference in how the constrained and unconstrained models make predictions for a patient, the more apparent the difference is in clinical interpretation.

Quantile Regression with Large Language Models for Price Prediction

Large Language Models (LLMs) have shown promise in structured prediction tasks, including regression, but existing approaches primarily focus on point estimates and lack systematic comparison across different methods. We investigate probabilistic regression using LLMs for unstructured inputs, addressing challenging text-to-distribution prediction tasks such as price estimation where both nuanced text understanding and uncertainty quantification are critical. We propose a novel quantile regression approach that enables LLMs to produce full predictive distributions, improving upon traditional point estimates. Through extensive experiments across three diverse price prediction datasets, we demonstrate that a Mistral-7B model fine-tuned with quantile heads significantly outperforms traditional approaches for both point and distributional estimations, as measured by three established metrics each for prediction accuracy and distributional calibration. Our systematic comparison of LLM approaches, model architectures, training approaches, and data scaling reveals that Mistral-7B consistently outperforms encoder architectures, embedding-based methods, and few-shot learning methods. Our experiments also reveal the effectiveness of LLM-assisted label correction in achieving human-level accuracy without systematic bias. Our curated datasets are made available at https://github.com/vnik18/llm-price-quantile-reg/ to support future research.

Can We Validate Counterfactual Estimations in the Presence of General Network Interference?

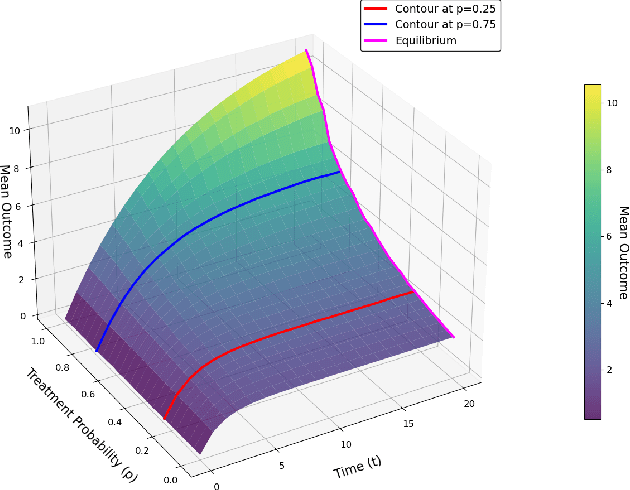
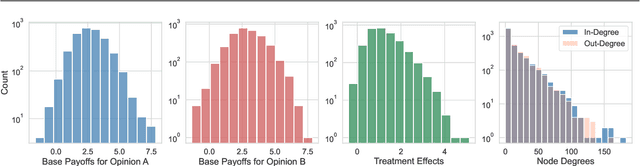
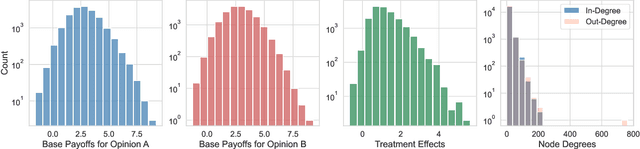
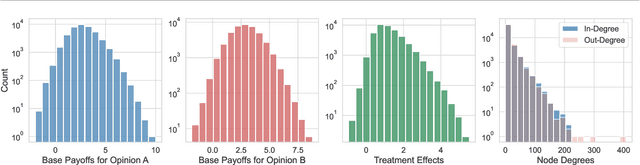
In experimental settings with network interference, a unit's treatment can influence outcomes of other units, challenging both causal effect estimation and its validation. Classic validation approaches fail as outcomes are only observable under one treatment scenario and exhibit complex correlation patterns due to interference. To address these challenges, we introduce a new framework enabling cross-validation for counterfactual estimation. At its core is our distribution-preserving network bootstrap method -- a theoretically-grounded approach inspired by approximate message passing. This method creates multiple subpopulations while preserving the underlying distribution of network effects. We extend recent causal message-passing developments by incorporating heterogeneous unit-level characteristics and varying local interactions, ensuring reliable finite-sample performance through non-asymptotic analysis. We also develop and publicly release a comprehensive benchmark toolbox with diverse experimental environments, from networks of interacting AI agents to opinion formation in real-world communities and ride-sharing applications. These environments provide known ground truth values while maintaining realistic complexities, enabling systematic examination of causal inference methods. Extensive evaluation across these environments demonstrates our method's robustness to diverse forms of network interference. Our work provides researchers with both a practical estimation framework and a standardized platform for testing future methodological developments.

Post Launch Evaluation of Policies in a High-Dimensional Setting

A/B tests, also known as randomized controlled experiments (RCTs), are the gold standard for evaluating the impact of new policies, products, or decisions. However, these tests can be costly in terms of time and resources, potentially exposing users, customers, or other test subjects (units) to inferior options. This paper explores practical considerations in applying methodologies inspired by "synthetic control" as an alternative to traditional A/B testing in settings with very large numbers of units, involving up to hundreds of millions of units, which is common in modern applications such as e-commerce and ride-sharing platforms. This method is particularly valuable in settings where the treatment affects only a subset of units, leaving many units unaffected. In these scenarios, synthetic control methods leverage data from unaffected units to estimate counterfactual outcomes for treated units. After the treatment is implemented, these estimates can be compared to actual outcomes to measure the treatment effect. A key challenge in creating accurate counterfactual outcomes is interpolation bias, a well-documented phenomenon that occurs when control units differ significantly from treated units. To address this, we propose a two-phase approach: first using nearest neighbor matching based on unit covariates to select similar control units, then applying supervised learning methods suitable for high-dimensional data to estimate counterfactual outcomes. Testing using six large-scale experiments demonstrates that this approach successfully improves estimate accuracy. However, our analysis reveals that machine learning bias -- which arises from methods that trade off bias for variance reduction -- can impact results and affect conclusions about treatment effects. We document this bias in large-scale experimental settings and propose effective de-biasing techniques to address this challenge.

Higher-Order Causal Message Passing for Experimentation with Complex Interference

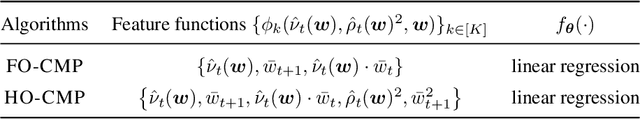
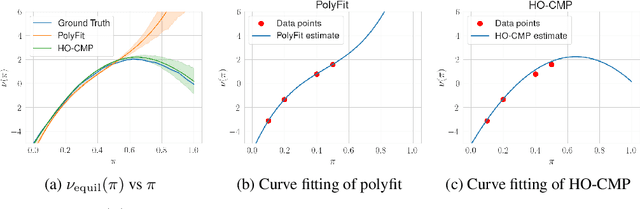
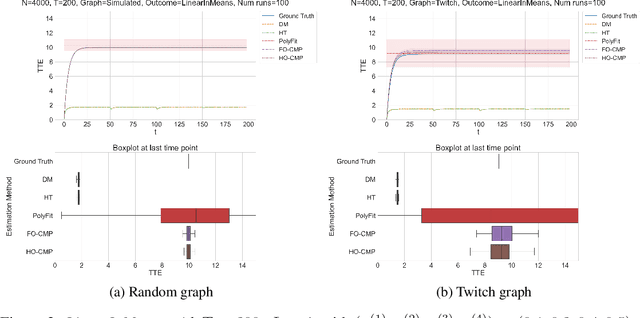
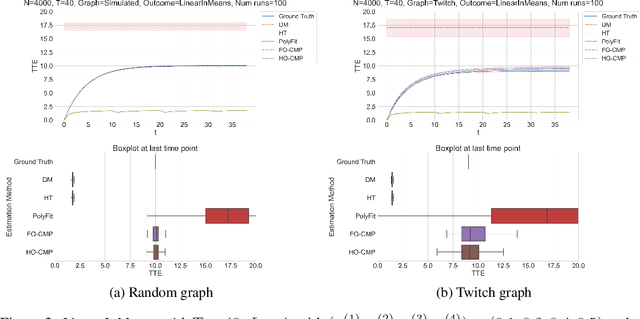
Accurate estimation of treatment effects is essential for decision-making across various scientific fields. This task, however, becomes challenging in areas like social sciences and online marketplaces, where treating one experimental unit can influence outcomes for others through direct or indirect interactions. Such interference can lead to biased treatment effect estimates, particularly when the structure of these interactions is unknown. We address this challenge by introducing a new class of estimators based on causal message-passing, specifically designed for settings with pervasive, unknown interference. Our estimator draws on information from the sample mean and variance of unit outcomes and treatments over time, enabling efficient use of observed data to estimate the evolution of the system state. Concretely, we construct non-linear features from the moments of unit outcomes and treatments and then learn a function that maps these features to future mean and variance of unit outcomes. This allows for the estimation of the treatment effect over time. Extensive simulations across multiple domains, using synthetic and real network data, demonstrate the efficacy of our approach in estimating total treatment effect dynamics, even in cases where interference exhibits non-monotonic behavior in the probability of treatment.

Aligning Model Properties via Conformal Risk Control

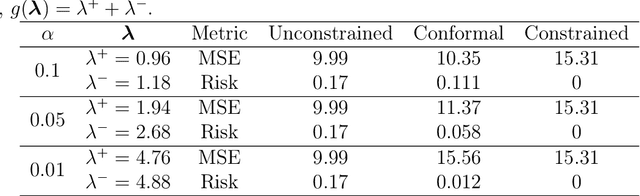
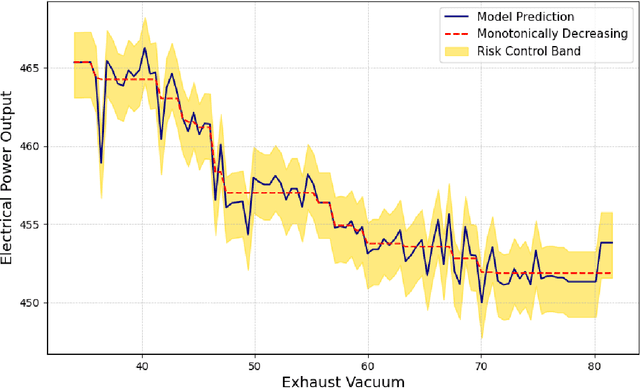
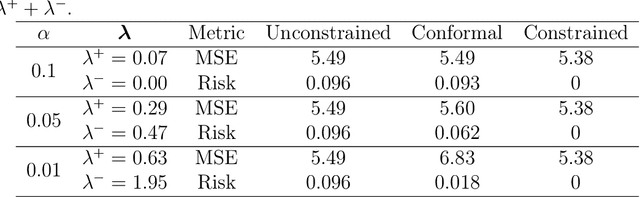
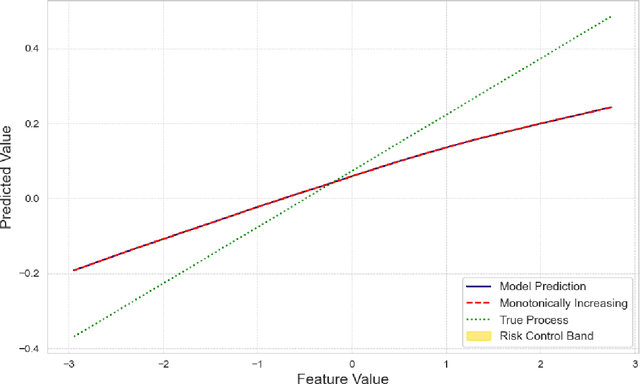
AI model alignment is crucial due to inadvertent biases in training data and the underspecified pipeline in modern machine learning, where numerous models with excellent test set metrics can be produced, yet they may not meet end-user requirements. Recent advances demonstrate that post-training model alignment via human feedback can address some of these challenges. However, these methods are often confined to settings (such as generative AI) where humans can interpret model outputs and provide feedback. In traditional non-generative settings, where model outputs are numerical values or classes, detecting misalignment through single-sample outputs is highly challenging. In this paper we consider an alternative strategy. We propose interpreting model alignment through property testing, defining an aligned model $f$ as one belonging to a subset $\mathcal{P}$ of functions that exhibit specific desired behaviors. We focus on post-processing a pre-trained model $f$ to better align with $\mathcal{P}$ using conformal risk control. Specifically, we develop a general procedure for converting queries for a given property $\mathcal{P}$ to a collection of loss functions suitable for use in a conformal risk control algorithm. We prove a probabilistic guarantee that the resulting conformal interval around $f$ contains a function approximately satisfying $\mathcal{P}$. Given the capabilities of modern AI models with extensive parameters and training data, one might assume alignment issues will resolve naturally. However, increasing training data or parameters in a random feature model doesn't eliminate the need for alignment techniques when pre-training data is biased. We demonstrate our alignment methodology on supervised learning datasets for properties like monotonicity and concavity. Our flexible procedure can be applied to various desired properties.