Thompson Sampling Efficiently Learns to Control Diffusion Processes

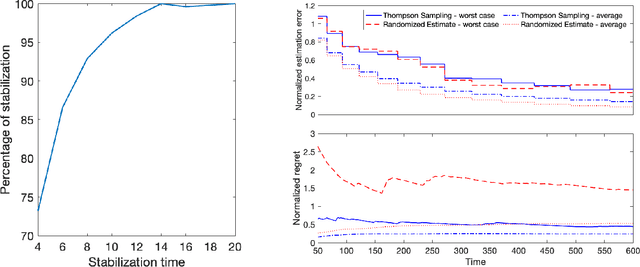
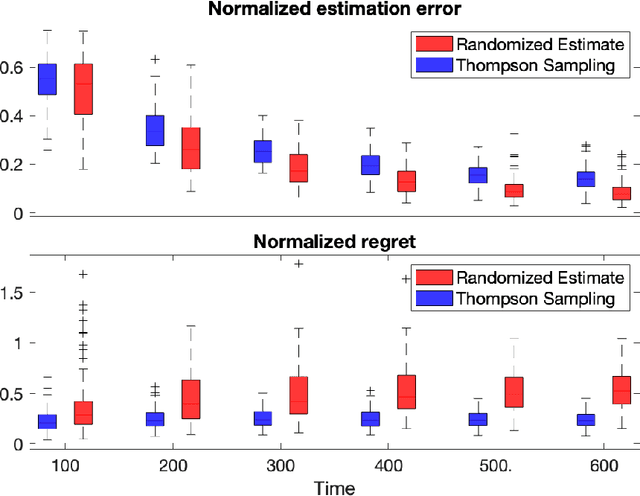
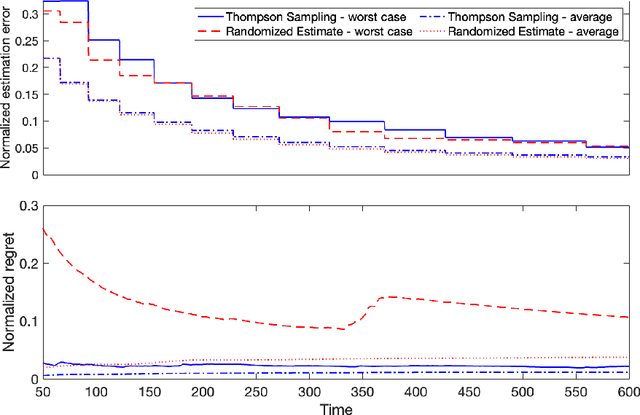
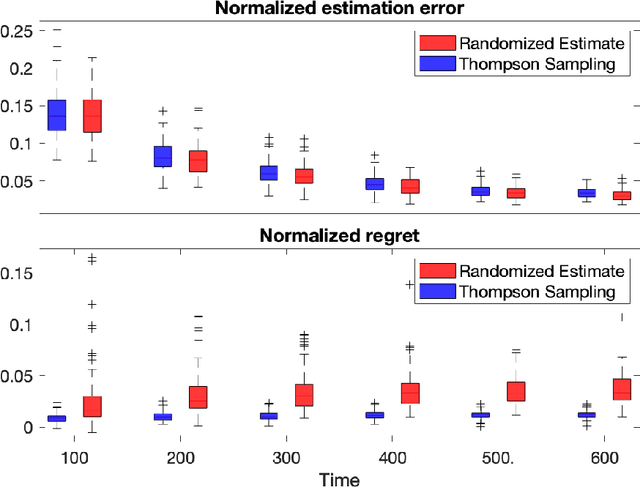
Diffusion processes that evolve according to linear stochastic differential equations are an important family of continuous-time dynamic decision-making models. Optimal policies are well-studied for them, under full certainty about the drift matrices. However, little is known about data-driven control of diffusion processes with uncertain drift matrices as conventional discrete-time analysis techniques are not applicable. In addition, while the task can be viewed as a reinforcement learning problem involving exploration and exploitation trade-off, ensuring system stability is a fundamental component of designing optimal policies. We establish that the popular Thompson sampling algorithm learns optimal actions fast, incurring only a square-root of time regret, and also stabilizes the system in a short time period. To the best of our knowledge, this is the first such result for Thompson sampling in a diffusion process control problem. We validate our theoretical results through empirical simulations with real parameter matrices from two settings of airplane and blood glucose control. Moreover, we observe that Thompson sampling significantly improves (worst-case) regret, compared to the state-of-the-art algorithms, suggesting Thompson sampling explores in a more guarded fashion. Our theoretical analysis involves characterization of a certain optimality manifold that ties the local geometry of the drift parameters to the optimal control of the diffusion process. We expect this technique to be of broader interest.

Bayesian Algorithms Learn to Stabilize Unknown Continuous-Time Systems

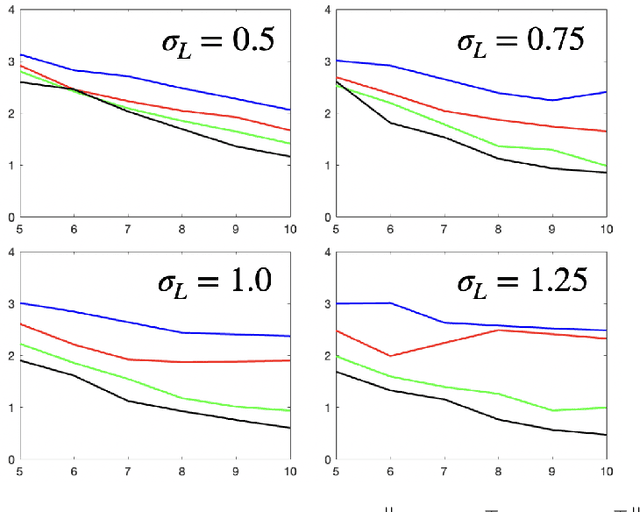
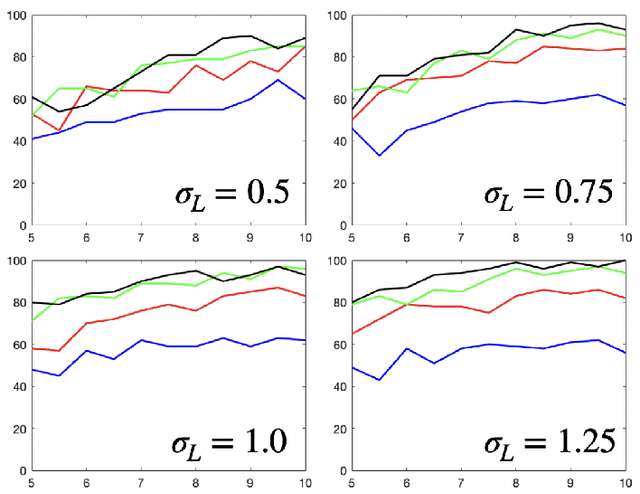
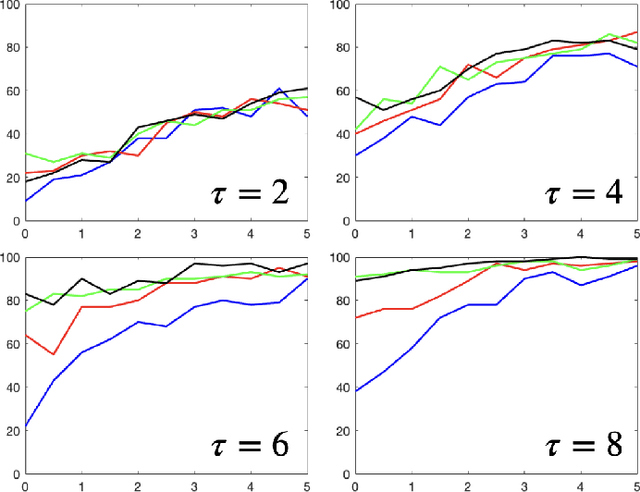
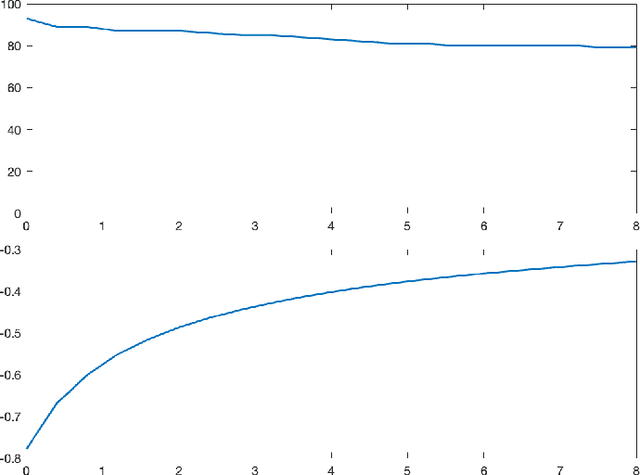
Linear dynamical systems are canonical models for learning-based control of plants with uncertain dynamics. The setting consists of a stochastic differential equation that captures the state evolution of the plant understudy, while the true dynamics matrices are unknown and need to be learned from the observed data of state trajectory. An important issue is to ensure that the system is stabilized and destabilizing control actions due to model uncertainties are precluded as soon as possible. A reliable stabilization procedure for this purpose that can effectively learn from unstable data to stabilize the system in a finite time is not currently available. In this work, we propose a novel Bayesian learning algorithm that stabilizes unknown continuous-time stochastic linear systems. The presented algorithm is flexible and exposes effective stabilization performance after a remarkably short time period of interacting with the system.

Efficient Estimation and Control of Unknown Stochastic Differential Equations

Ito stochastic differential equations are ubiquitous models for dynamic environments. A canonical problem in this setting is that of decision-making policies for systems that evolve according to unknown diffusion processes. The goals consist of design and analysis of efficient policies for both minimizing quadratic cost functions of states and actions, as well as accurate estimation of underlying linear dynamics. Despite recent advances in statistical decision theory, little is known about estimation and control of diffusion processes, which is the subject of this work. A fundamental challenge is that the policy needs to continuously address the exploration-exploitation dilemma; estimation accuracy is necessary for optimal decision-making, while sub-optimal actions are required for obtaining accurate estimates. We present an easy-to-implement reinforcement learning algorithm and establish theoretical performance guarantees showing that it efficiently addresses the above dilemma. In fact, the proposed algorithm learns the true diffusion process and optimal actions fast, such that the per-unit-time increase in cost decays with the square-root rate as time grows. Further, we present tight results for assuring system stability and for specifying fundamental limits of sub-optimalities caused by uncertainties. To obtain the results, multiple novel methods are developed for analysis of matrix perturbations, for studying comparative ratios of stochastic integrals and spectral properties of random matrices, and the new framework of policy differentiation is proposed.

Adaptive Control of Quadratic Costs in Linear Stochastic Differential Equations

We study a canonical problem in adaptive control; design and analysis of policies for minimizing quadratic costs in unknown continuous-time linear dynamical systems. We address important challenges including accuracy of learning the unknown parameters of the underlying stochastic differential equation, as well as full analyses of performance degradation due to sub-optimal actions (i.e., regret). Then, an easy-to-implement algorithm for balancing exploration versus exploitation is proposed, followed by theoretical guarantees showing a square-root of time regret bound. Further, we present tight results for assuring system stability and for specifying fundamental limits for regret. To establish the presented results, multiple novel technical frameworks are developed, which can be of independent interests.