Bayesian Algorithms Learn to Stabilize Unknown Continuous-Time Systems
Paper and Code
Dec 30, 2021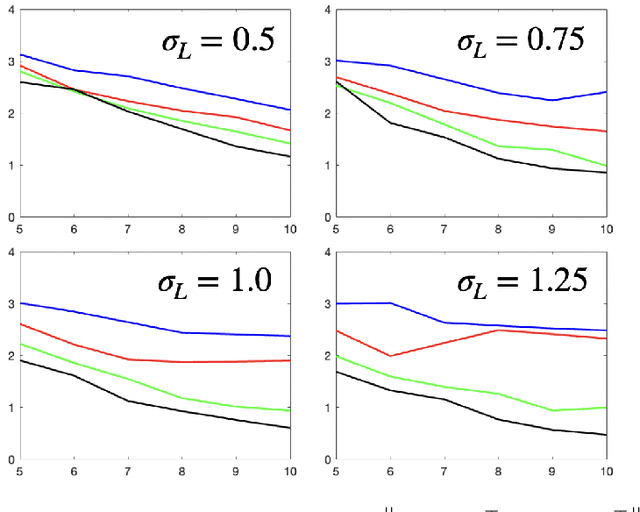
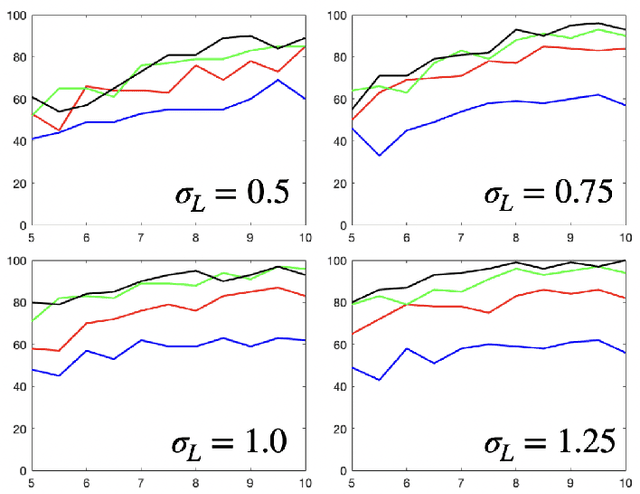
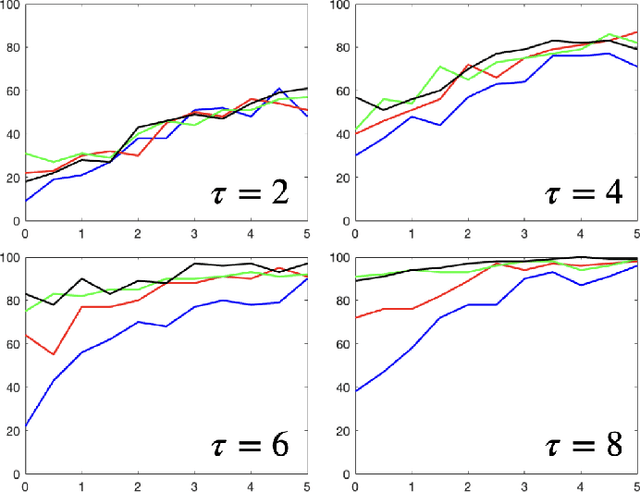
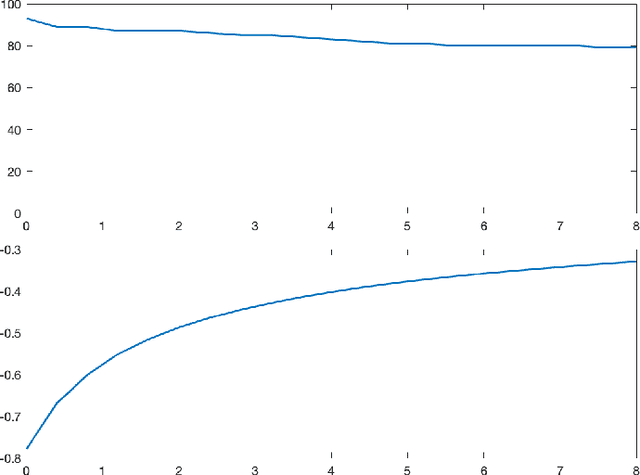
Linear dynamical systems are canonical models for learning-based control of plants with uncertain dynamics. The setting consists of a stochastic differential equation that captures the state evolution of the plant understudy, while the true dynamics matrices are unknown and need to be learned from the observed data of state trajectory. An important issue is to ensure that the system is stabilized and destabilizing control actions due to model uncertainties are precluded as soon as possible. A reliable stabilization procedure for this purpose that can effectively learn from unstable data to stabilize the system in a finite time is not currently available. In this work, we propose a novel Bayesian learning algorithm that stabilizes unknown continuous-time stochastic linear systems. The presented algorithm is flexible and exposes effective stabilization performance after a remarkably short time period of interacting with the system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge