Thompson Sampling in Partially Observable Contextual Bandits

Contextual bandits constitute a classical framework for decision-making under uncertainty. In this setting, the goal is to learn the arms of highest reward subject to contextual information, while the unknown reward parameters of each arm need to be learned by experimenting that specific arm. Accordingly, a fundamental problem is that of balancing exploration (i.e., pulling different arms to learn their parameters), versus exploitation (i.e., pulling the best arms to gain reward). To study this problem, the existing literature mostly considers perfectly observed contexts. However, the setting of partial context observations remains unexplored to date, despite being theoretically more general and practically more versatile. We study bandit policies for learning to select optimal arms based on the data of observations, which are noisy linear functions of the unobserved context vectors. Our theoretical analysis shows that the Thompson sampling policy successfully balances exploration and exploitation. Specifically, we establish the followings: (i) regret bounds that grow poly-logarithmically with time, (ii) square-root consistency of parameter estimation, and (iii) scaling of the regret with other quantities including dimensions and number of arms. Extensive numerical experiments with both real and synthetic data are presented as well, corroborating the efficacy of Thompson sampling. To establish the results, we introduce novel martingale techniques and concentration inequalities to address partially observed dependent random variables generated from unspecified distributions, and also leverage problem-dependent information to sharpen probabilistic bounds for time-varying suboptimality gaps. These techniques pave the road towards studying other decision-making problems with contextual information as well as partial observations.

Thompson Sampling Efficiently Learns to Control Diffusion Processes

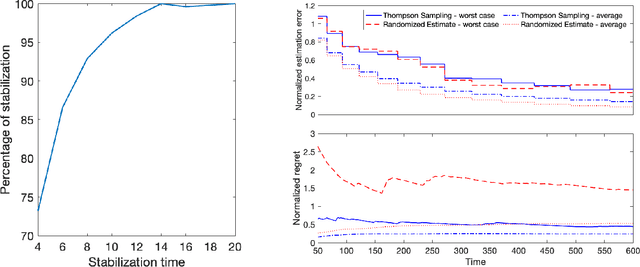
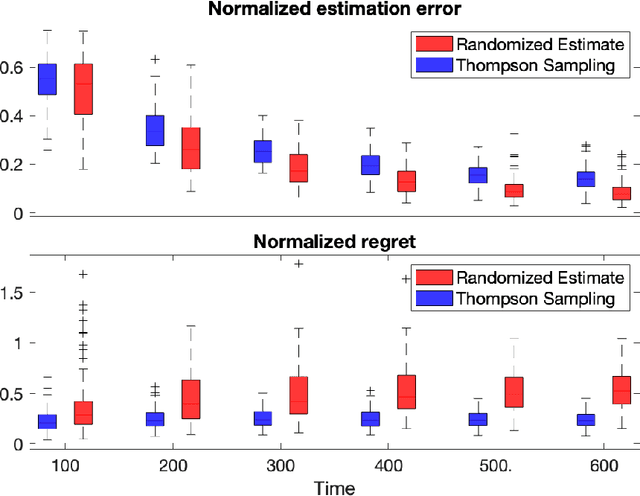
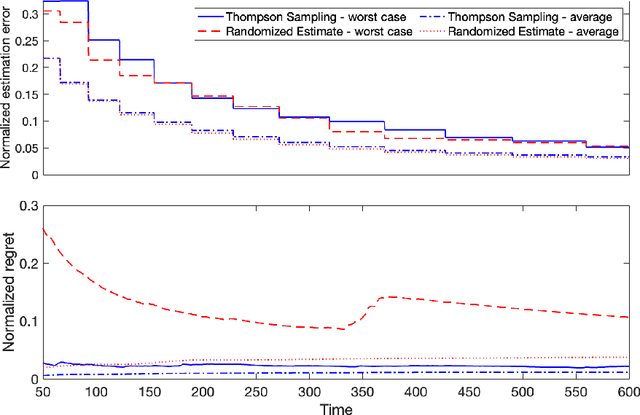
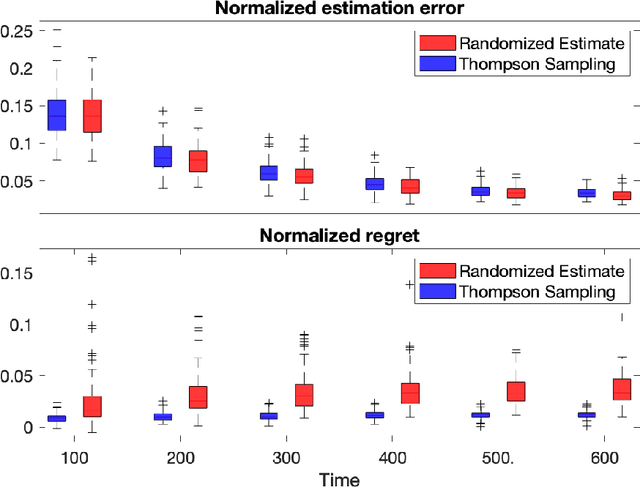
Diffusion processes that evolve according to linear stochastic differential equations are an important family of continuous-time dynamic decision-making models. Optimal policies are well-studied for them, under full certainty about the drift matrices. However, little is known about data-driven control of diffusion processes with uncertain drift matrices as conventional discrete-time analysis techniques are not applicable. In addition, while the task can be viewed as a reinforcement learning problem involving exploration and exploitation trade-off, ensuring system stability is a fundamental component of designing optimal policies. We establish that the popular Thompson sampling algorithm learns optimal actions fast, incurring only a square-root of time regret, and also stabilizes the system in a short time period. To the best of our knowledge, this is the first such result for Thompson sampling in a diffusion process control problem. We validate our theoretical results through empirical simulations with real parameter matrices from two settings of airplane and blood glucose control. Moreover, we observe that Thompson sampling significantly improves (worst-case) regret, compared to the state-of-the-art algorithms, suggesting Thompson sampling explores in a more guarded fashion. Our theoretical analysis involves characterization of a certain optimality manifold that ties the local geometry of the drift parameters to the optimal control of the diffusion process. We expect this technique to be of broader interest.

Regret Analysis of Certainty Equivalence Policies in Continuous-Time Linear-Quadratic Systems

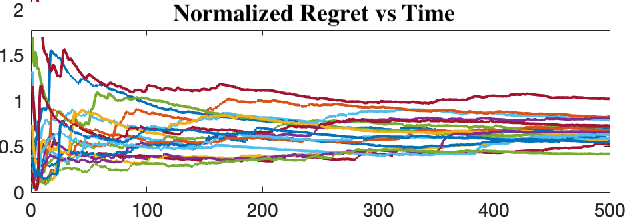
This work studies theoretical performance guarantees of a ubiquitous reinforcement learning policy for controlling the canonical model of stochastic linear-quadratic system. We show that randomized certainty equivalent policy addresses the exploration-exploitation dilemma for minimizing quadratic costs in linear dynamical systems that evolve according to stochastic differential equations. More precisely, we establish square-root of time regret bounds, indicating that randomized certainty equivalent policy learns optimal control actions fast from a single state trajectory. Further, linear scaling of the regret with the number of parameters is shown. The presented analysis introduces novel and useful technical approaches, and sheds light on fundamental challenges of continuous-time reinforcement learning.

Worst-case Performance of Greedy Policies in Bandits with Imperfect Context Observations

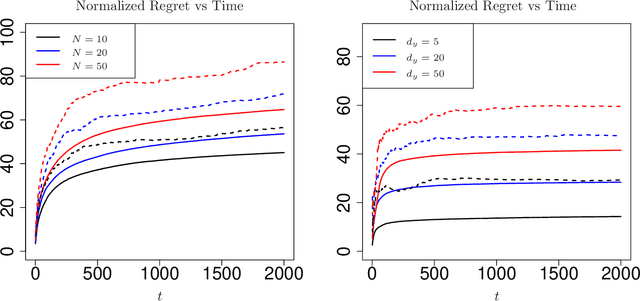
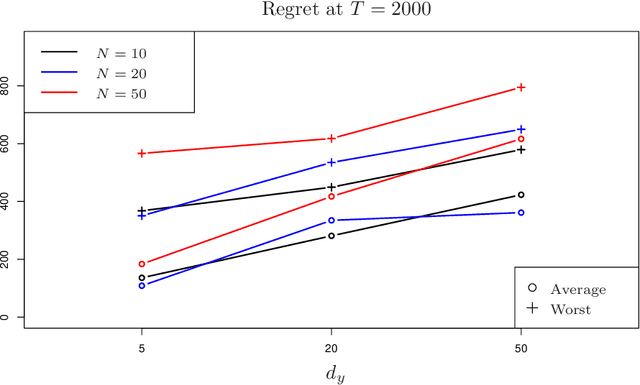
Contextual bandits are canonical models for sequential decision-making under uncertainty in environments with time-varying components. In this setting, the expected reward of each bandit arm consists of the inner product of an unknown parameter and the context vector of that arm, perturbed with a random error. The classical setting heavily relies on fully observed contexts, while study of the richer model of imperfectly observed contextual bandits is immature. This work considers Greedy reinforcement learning policies that take actions as if the current estimates of the parameter and of the unobserved contexts coincide with the corresponding true values. We establish that the non-asymptotic worst-case regret grows logarithmically with the time horizon and the failure probability, while it scales linearly with the number of arms. Numerical analysis showcasing the above efficiency of Greedy policies is also provided.

Efficient Algorithms for Learning to Control Bandits with Unobserved Contexts

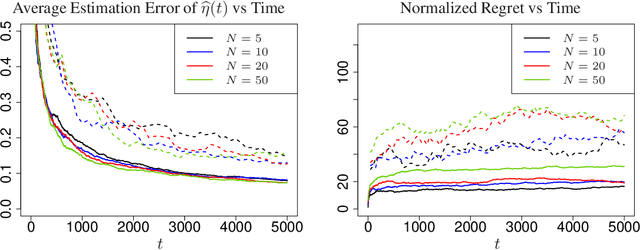
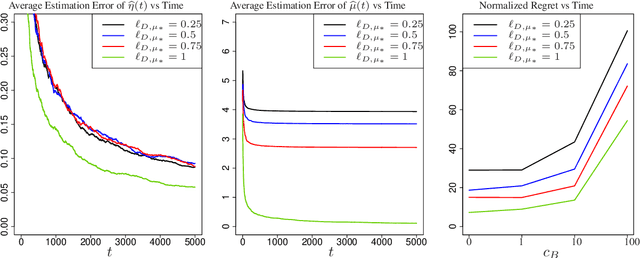
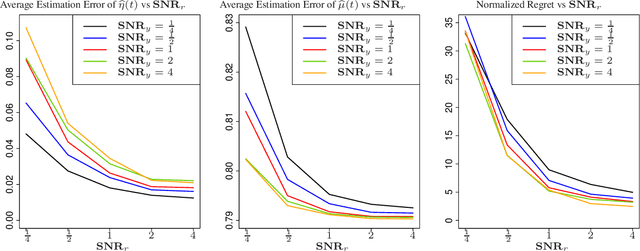
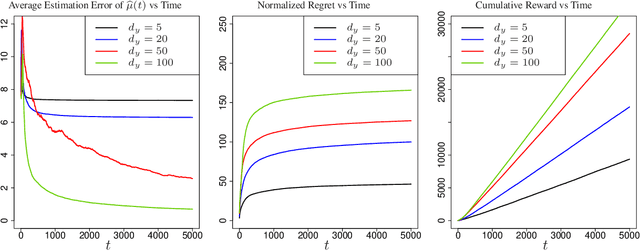
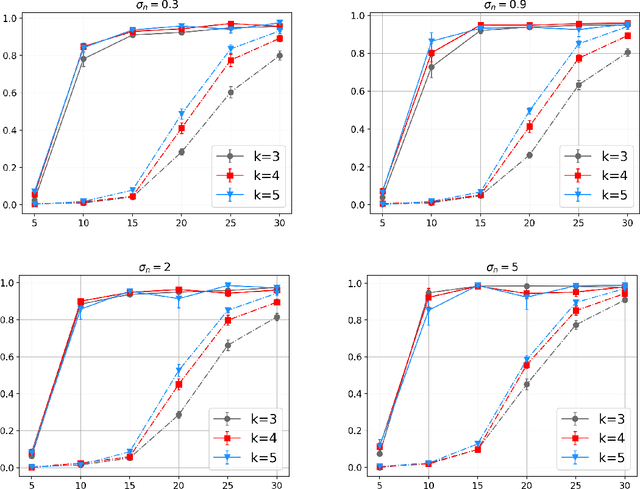
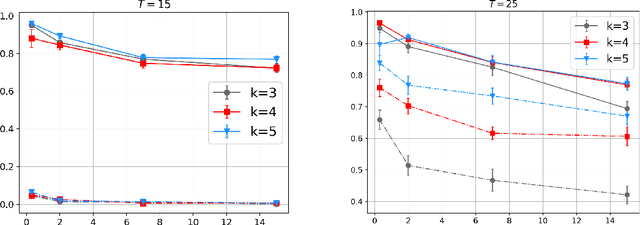
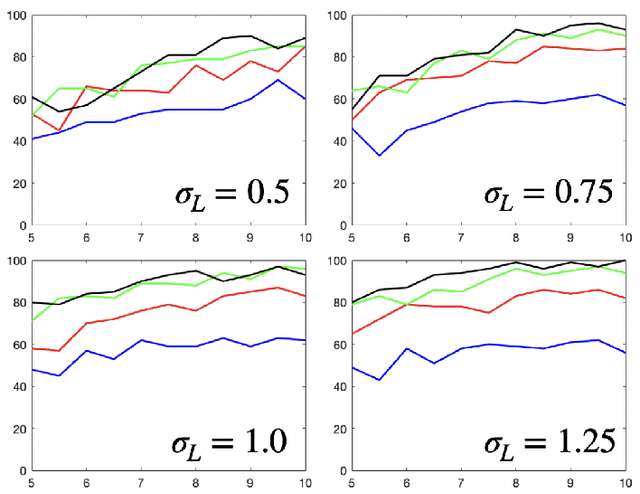
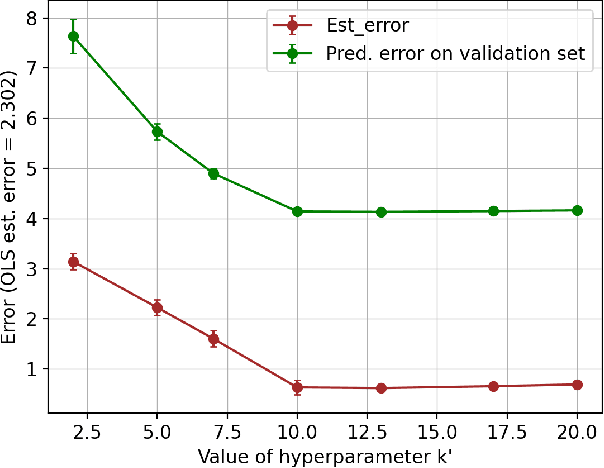
Contextual bandits are widely-used in the study of learning-based control policies for finite action spaces. While the problem is well-studied for bandits with perfectly observed context vectors, little is known about the case of imperfectly observed contexts. For this setting, existing approaches are inapplicable and new conceptual and technical frameworks are required. We present an implementable posterior sampling algorithm for bandits with imperfect context observations and study its performance for learning optimal decisions. The provided numerical results relate the performance of the algorithm to different quantities of interest including the number of arms, dimensions, observation matrices, posterior rescaling factors, and signal-to-noise ratios. In general, the proposed algorithm exposes efficiency in learning from the noisy imperfect observations and taking actions accordingly. Enlightening understandings the analyses provide as well as interesting future directions it points to, are discussed as well.

Joint Learning-Based Stabilization of Multiple Unknown Linear Systems

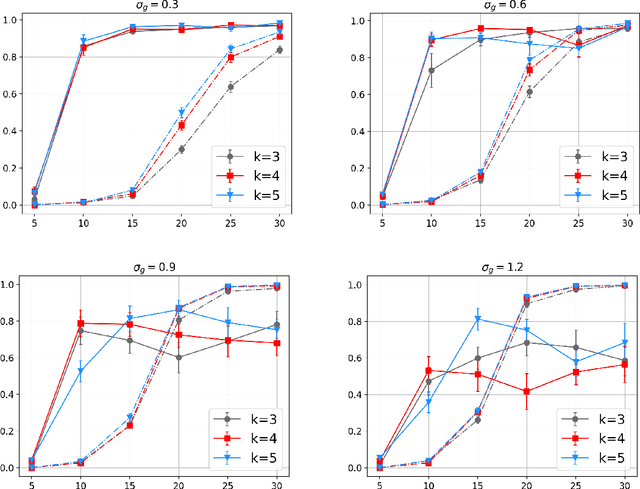
Learning-based control of linear systems received a lot of attentions recently. In popular settings, the true dynamical models are unknown to the decision-maker and need to be interactively learned by applying control inputs to the systems. Unlike the matured literature of efficient reinforcement learning policies for adaptive control of a single system, results on joint learning of multiple systems are not currently available. Especially, the important problem of fast and reliable joint-stabilization remains unaddressed and so is the focus of this work. We propose a novel joint learning-based stabilization algorithm for quickly learning stabilizing policies for all systems understudy, from the data of unstable state trajectories. The presented procedure is shown to be notably effective such that it stabilizes the family of dynamical systems in an extremely short time period.

Bayesian Algorithms Learn to Stabilize Unknown Continuous-Time Systems

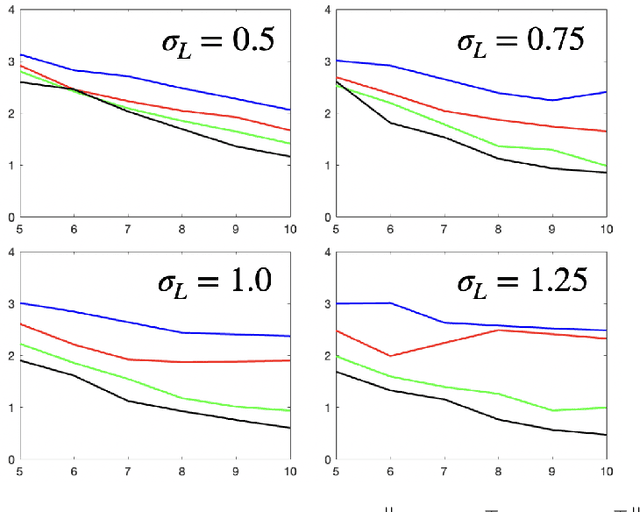
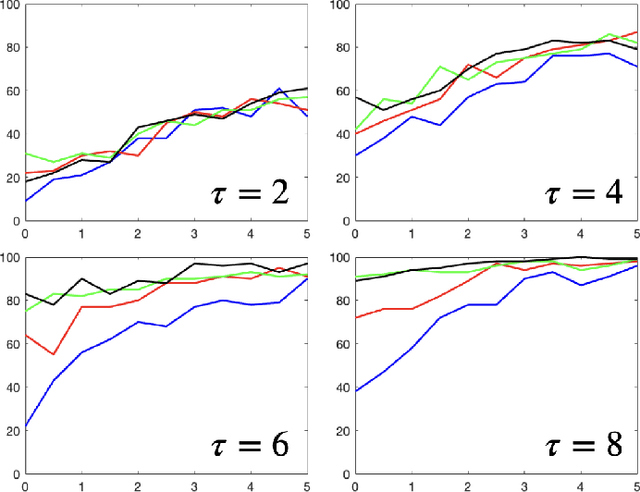
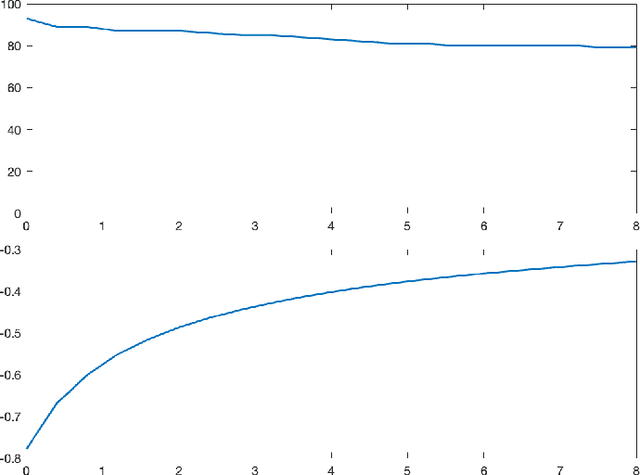
Linear dynamical systems are canonical models for learning-based control of plants with uncertain dynamics. The setting consists of a stochastic differential equation that captures the state evolution of the plant understudy, while the true dynamics matrices are unknown and need to be learned from the observed data of state trajectory. An important issue is to ensure that the system is stabilized and destabilizing control actions due to model uncertainties are precluded as soon as possible. A reliable stabilization procedure for this purpose that can effectively learn from unstable data to stabilize the system in a finite time is not currently available. In this work, we propose a novel Bayesian learning algorithm that stabilizes unknown continuous-time stochastic linear systems. The presented algorithm is flexible and exposes effective stabilization performance after a remarkably short time period of interacting with the system.

Joint Learning of Linear Time-Invariant Dynamical Systems

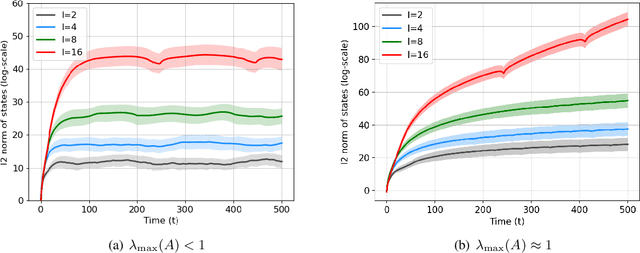
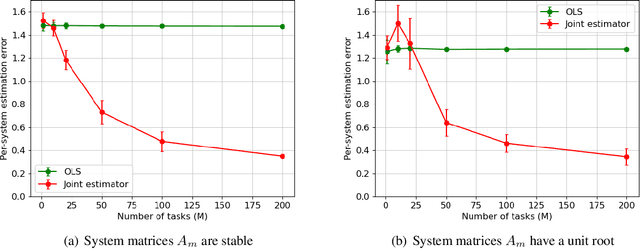
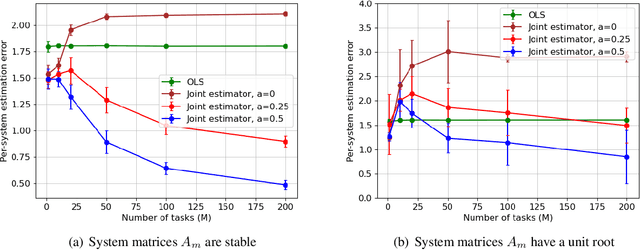
Learning the parameters of a linear time-invariant dynamical system (LTIDS) is a problem of current interest. In many applications, one is interested in jointly learning the parameters of multiple related LTIDS, which remains unexplored to date. To that end, we develop a joint estimator for learning the transition matrices of LTIDS that share common basis matrices. Further, we establish finite-time error bounds that depend on the underlying sample size, dimension, number of tasks, and spectral properties of the transition matrices. The results are obtained under mild regularity assumptions and showcase the gains from pooling information across LTIDS, in comparison to learning each system separately. We also study the impact of misspecifying the joint structure of the transition matrices and show that the established results are robust in the presence of moderate misspecifications.

Analysis of Thompson Sampling for Partially Observable Contextual Multi-Armed Bandits

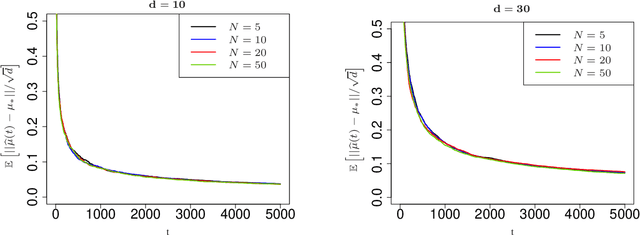
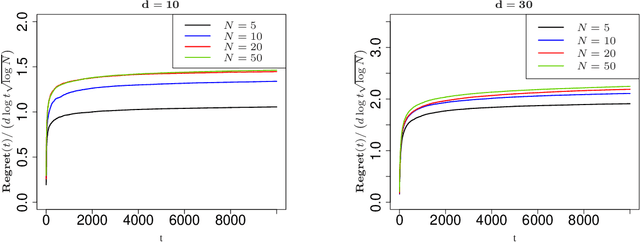
Contextual multi-armed bandits are classical models in reinforcement learning for sequential decision-making associated with individual information. A widely-used policy for bandits is Thompson Sampling, where samples from a data-driven probabilistic belief about unknown parameters are used to select the control actions. For this computationally fast algorithm, performance analyses are available under full context-observations. However, little is known for problems that contexts are not fully observed. We propose a Thompson Sampling algorithm for partially observable contextual multi-armed bandits, and establish theoretical performance guarantees. Technically, we show that the regret of the presented policy scales logarithmically with time and the number of arms, and linearly with the dimension. Further, we establish rates of learning unknown parameters, and provide illustrative numerical analyses.

Efficient Estimation and Control of Unknown Stochastic Differential Equations

Ito stochastic differential equations are ubiquitous models for dynamic environments. A canonical problem in this setting is that of decision-making policies for systems that evolve according to unknown diffusion processes. The goals consist of design and analysis of efficient policies for both minimizing quadratic cost functions of states and actions, as well as accurate estimation of underlying linear dynamics. Despite recent advances in statistical decision theory, little is known about estimation and control of diffusion processes, which is the subject of this work. A fundamental challenge is that the policy needs to continuously address the exploration-exploitation dilemma; estimation accuracy is necessary for optimal decision-making, while sub-optimal actions are required for obtaining accurate estimates. We present an easy-to-implement reinforcement learning algorithm and establish theoretical performance guarantees showing that it efficiently addresses the above dilemma. In fact, the proposed algorithm learns the true diffusion process and optimal actions fast, such that the per-unit-time increase in cost decays with the square-root rate as time grows. Further, we present tight results for assuring system stability and for specifying fundamental limits of sub-optimalities caused by uncertainties. To obtain the results, multiple novel methods are developed for analysis of matrix perturbations, for studying comparative ratios of stochastic integrals and spectral properties of random matrices, and the new framework of policy differentiation is proposed.