Graph Canonical Correlation Analysis

Canonical correlation analysis (CCA) is a widely used technique for estimating associations between two sets of multi-dimensional variables. Recent advancements in CCA methods have expanded their application to decipher the interactions of multiomics datasets, imaging-omics datasets, and more. However, conventional CCA methods are limited in their ability to incorporate structured patterns in the cross-correlation matrix, potentially leading to suboptimal estimations. To address this limitation, we propose the graph Canonical Correlation Analysis (gCCA) approach, which calculates canonical correlations based on the graph structure of the cross-correlation matrix between the two sets of variables. We develop computationally efficient algorithms for gCCA, and provide theoretical results for finite sample analysis of best subset selection and canonical correlation estimation by introducing concentration inequalities and stopping time rule based on martingale theories. Extensive simulations demonstrate that gCCA outperforms competing CCA methods. Additionally, we apply gCCA to a multiomics dataset of DNA methylation and RNA-seq transcriptomics, identifying both positively and negatively regulated gene expression pathways by DNA methylation pathways.

Thompson Sampling in Partially Observable Contextual Bandits

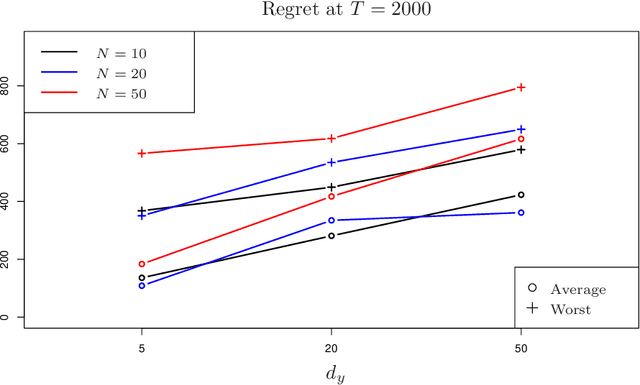
Contextual bandits constitute a classical framework for decision-making under uncertainty. In this setting, the goal is to learn the arms of highest reward subject to contextual information, while the unknown reward parameters of each arm need to be learned by experimenting that specific arm. Accordingly, a fundamental problem is that of balancing exploration (i.e., pulling different arms to learn their parameters), versus exploitation (i.e., pulling the best arms to gain reward). To study this problem, the existing literature mostly considers perfectly observed contexts. However, the setting of partial context observations remains unexplored to date, despite being theoretically more general and practically more versatile. We study bandit policies for learning to select optimal arms based on the data of observations, which are noisy linear functions of the unobserved context vectors. Our theoretical analysis shows that the Thompson sampling policy successfully balances exploration and exploitation. Specifically, we establish the followings: (i) regret bounds that grow poly-logarithmically with time, (ii) square-root consistency of parameter estimation, and (iii) scaling of the regret with other quantities including dimensions and number of arms. Extensive numerical experiments with both real and synthetic data are presented as well, corroborating the efficacy of Thompson sampling. To establish the results, we introduce novel martingale techniques and concentration inequalities to address partially observed dependent random variables generated from unspecified distributions, and also leverage problem-dependent information to sharpen probabilistic bounds for time-varying suboptimality gaps. These techniques pave the road towards studying other decision-making problems with contextual information as well as partial observations.

Worst-case Performance of Greedy Policies in Bandits with Imperfect Context Observations

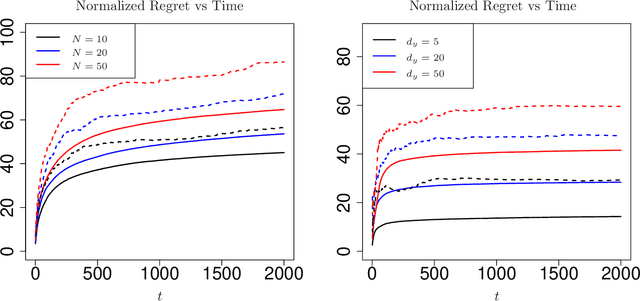
Contextual bandits are canonical models for sequential decision-making under uncertainty in environments with time-varying components. In this setting, the expected reward of each bandit arm consists of the inner product of an unknown parameter and the context vector of that arm, perturbed with a random error. The classical setting heavily relies on fully observed contexts, while study of the richer model of imperfectly observed contextual bandits is immature. This work considers Greedy reinforcement learning policies that take actions as if the current estimates of the parameter and of the unobserved contexts coincide with the corresponding true values. We establish that the non-asymptotic worst-case regret grows logarithmically with the time horizon and the failure probability, while it scales linearly with the number of arms. Numerical analysis showcasing the above efficiency of Greedy policies is also provided.

Efficient Algorithms for Learning to Control Bandits with Unobserved Contexts

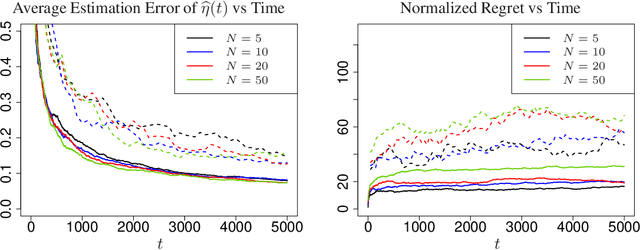
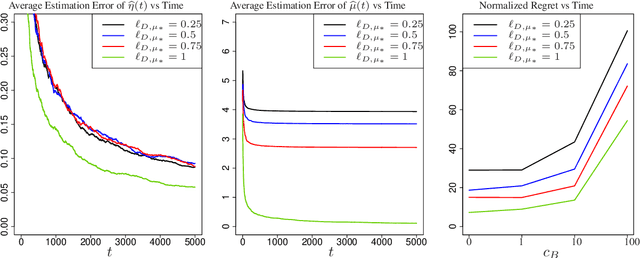
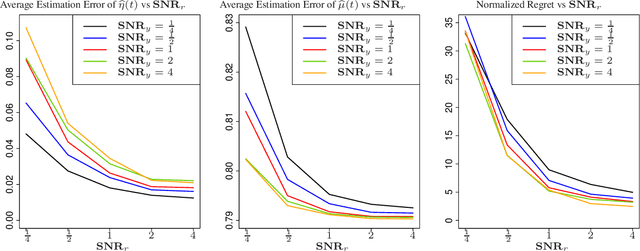
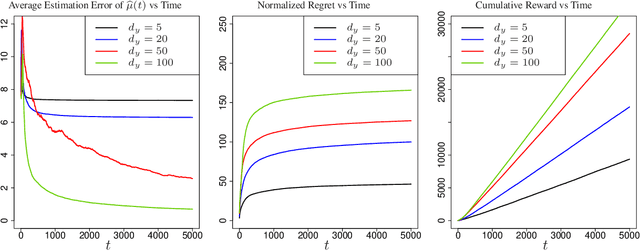
Contextual bandits are widely-used in the study of learning-based control policies for finite action spaces. While the problem is well-studied for bandits with perfectly observed context vectors, little is known about the case of imperfectly observed contexts. For this setting, existing approaches are inapplicable and new conceptual and technical frameworks are required. We present an implementable posterior sampling algorithm for bandits with imperfect context observations and study its performance for learning optimal decisions. The provided numerical results relate the performance of the algorithm to different quantities of interest including the number of arms, dimensions, observation matrices, posterior rescaling factors, and signal-to-noise ratios. In general, the proposed algorithm exposes efficiency in learning from the noisy imperfect observations and taking actions accordingly. Enlightening understandings the analyses provide as well as interesting future directions it points to, are discussed as well.

Analysis of Thompson Sampling for Partially Observable Contextual Multi-Armed Bandits

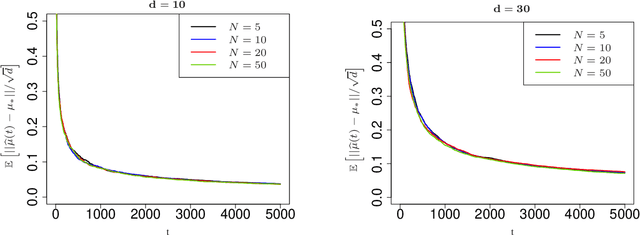
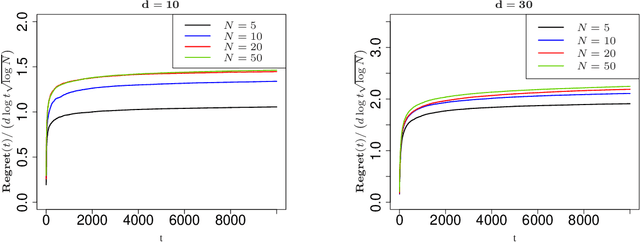
Contextual multi-armed bandits are classical models in reinforcement learning for sequential decision-making associated with individual information. A widely-used policy for bandits is Thompson Sampling, where samples from a data-driven probabilistic belief about unknown parameters are used to select the control actions. For this computationally fast algorithm, performance analyses are available under full context-observations. However, little is known for problems that contexts are not fully observed. We propose a Thompson Sampling algorithm for partially observable contextual multi-armed bandits, and establish theoretical performance guarantees. Technically, we show that the regret of the presented policy scales logarithmically with time and the number of arms, and linearly with the dimension. Further, we establish rates of learning unknown parameters, and provide illustrative numerical analyses.