Analysis of Thompson Sampling for Partially Observable Contextual Multi-Armed Bandits
Paper and Code
Oct 23, 2021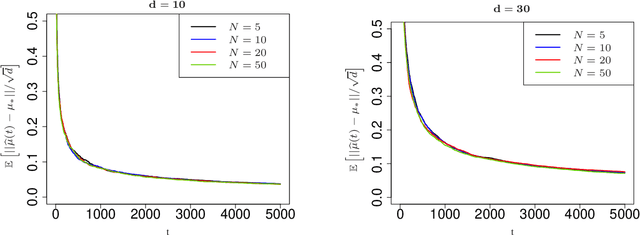
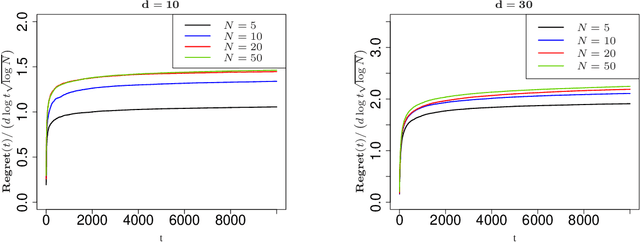
Contextual multi-armed bandits are classical models in reinforcement learning for sequential decision-making associated with individual information. A widely-used policy for bandits is Thompson Sampling, where samples from a data-driven probabilistic belief about unknown parameters are used to select the control actions. For this computationally fast algorithm, performance analyses are available under full context-observations. However, little is known for problems that contexts are not fully observed. We propose a Thompson Sampling algorithm for partially observable contextual multi-armed bandits, and establish theoretical performance guarantees. Technically, we show that the regret of the presented policy scales logarithmically with time and the number of arms, and linearly with the dimension. Further, we establish rates of learning unknown parameters, and provide illustrative numerical analyses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge