Worst-case Performance of Greedy Policies in Bandits with Imperfect Context Observations

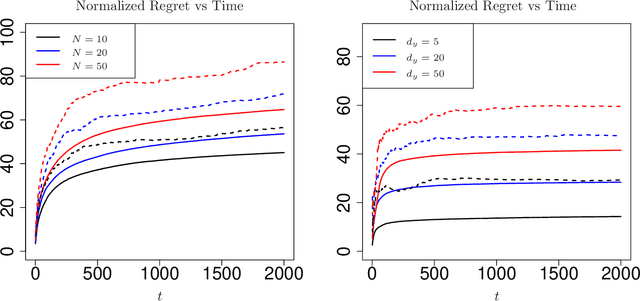
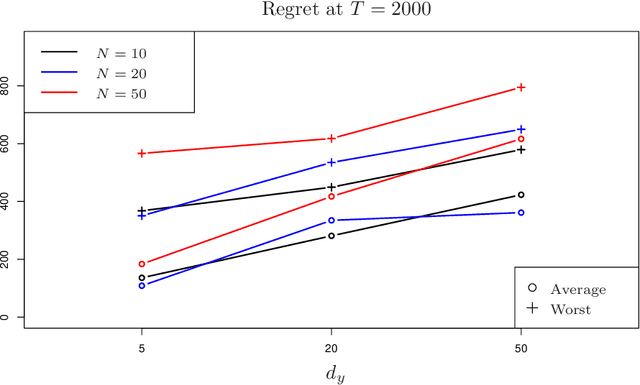
Contextual bandits are canonical models for sequential decision-making under uncertainty in environments with time-varying components. In this setting, the expected reward of each bandit arm consists of the inner product of an unknown parameter and the context vector of that arm, perturbed with a random error. The classical setting heavily relies on fully observed contexts, while study of the richer model of imperfectly observed contextual bandits is immature. This work considers Greedy reinforcement learning policies that take actions as if the current estimates of the parameter and of the unobserved contexts coincide with the corresponding true values. We establish that the non-asymptotic worst-case regret grows logarithmically with the time horizon and the failure probability, while it scales linearly with the number of arms. Numerical analysis showcasing the above efficiency of Greedy policies is also provided.