Graph Canonical Correlation Analysis

Canonical correlation analysis (CCA) is a widely used technique for estimating associations between two sets of multi-dimensional variables. Recent advancements in CCA methods have expanded their application to decipher the interactions of multiomics datasets, imaging-omics datasets, and more. However, conventional CCA methods are limited in their ability to incorporate structured patterns in the cross-correlation matrix, potentially leading to suboptimal estimations. To address this limitation, we propose the graph Canonical Correlation Analysis (gCCA) approach, which calculates canonical correlations based on the graph structure of the cross-correlation matrix between the two sets of variables. We develop computationally efficient algorithms for gCCA, and provide theoretical results for finite sample analysis of best subset selection and canonical correlation estimation by introducing concentration inequalities and stopping time rule based on martingale theories. Extensive simulations demonstrate that gCCA outperforms competing CCA methods. Additionally, we apply gCCA to a multiomics dataset of DNA methylation and RNA-seq transcriptomics, identifying both positively and negatively regulated gene expression pathways by DNA methylation pathways.

A Systematic Bias of Machine Learning Regression Models and Its Correction: an Application to Imaging-based Brain Age Prediction

Machine learning models for continuous outcomes often yield systematically biased predictions, particularly for values that largely deviate from the mean. Specifically, predictions for large-valued outcomes tend to be negatively biased, while those for small-valued outcomes are positively biased. We refer to this linear central tendency warped bias as the "systematic bias of machine learning regression". In this paper, we first demonstrate that this issue persists across various machine learning models, and then delve into its theoretical underpinnings. We propose a general constrained optimization approach designed to correct this bias and develop a computationally efficient algorithm to implement our method. Our simulation results indicate that our correction method effectively eliminates the bias from the predicted outcomes. We apply the proposed approach to the prediction of brain age using neuroimaging data. In comparison to competing machine learning models, our method effectively addresses the longstanding issue of "systematic bias of machine learning regression" in neuroimaging-based brain age calculation, yielding unbiased predictions of brain age.

Extrinsic Kernel Ridge Regression Classifier for Planar Kendall Shape Space

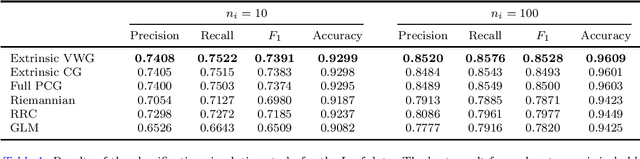
Kernel methods have had great success in the statistics and machine learning community. Despite their growing popularity, however, less effort has been drawn towards developing kernel based classification methods on manifold due to the non-Euclidean geometry. In this paper, motivated by the extrinsic framework of manifold-valued data analysis, we propose two types of new kernels on planar Kendall shape space $\Sigma_2^k$, called extrinsic Veronese Whitney Gaussian kernel and extrinsic complex Gaussian kernel. We show that our approach can be extended to develop Gaussian like kernels on any embedded manifold. Furthermore, kernel ridge regression classifier (KRRC) is implemented to address the shape classification problem on $\Sigma_2^k$, and their promising performances are illustrated through the real dataset.