Sampling the Swadesh List to Identify Similar Languages with Tree Spaces

Communication plays a vital role in human interaction. Studying language is a worthwhile task and more recently has become quantitative in nature with developments of fields like quantitative comparative linguistics and lexicostatistics. With respect to the authors own native languages, the ancestry of the English language and the Latin alphabet are of the primary interest. The Indo-European Tree traces many modern languages back to the Proto-Indo-European root. Swadesh's cognates played a large role in developing that historical perspective where some of the primary branches are Germanic, Celtic, Italic, and Balto-Slavic. This paper will use data analysis on open books where the simplest singular space is the 3-spider - a union T3 of three rays with their endpoints glued at a point 0 - which can represent these tree spaces for language clustering. These trees are built using a single linkage method for clustering based on distances between samples from languages which use the Latin Script. Taking three languages at a time, the barycenter is determined. Some initial results have found both non-sticky and sticky sample means. If the mean exhibits non-sticky properties, then one language may come from a different ancestor than the other two. If the mean is considered sticky, then the languages may share a common ancestor or all languages may have different ancestry.

Nonparametric Data Analysis on the Space of Perceived Colors

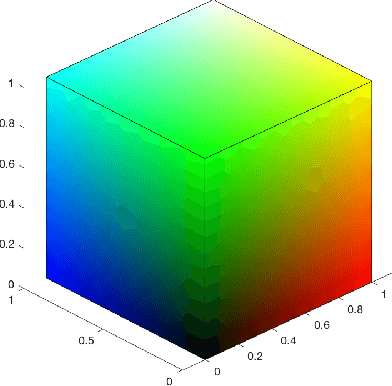
Moving around in a 3D world, requires the visual system of a living individual to rely on three channels of image recognition, which is done through three types of retinal cones. Newton, Grasmann, Helmholz and Schr$\ddot{o}$dinger laid down the basic assumptions needed to understand colored vision. Such concepts were furthered by Resnikoff, who imagined the space of perceived colors as a 3D homogeneous space. This article is concerned with perceived colors regarded as random objects on a Resnikoff 3D homogeneous space model. Two applications to color differentiation in machine vision are illustrated for the proposed statistical methodology, applied to the Euclidean model for perceived colors.

Extrinsic Kernel Ridge Regression Classifier for Planar Kendall Shape Space

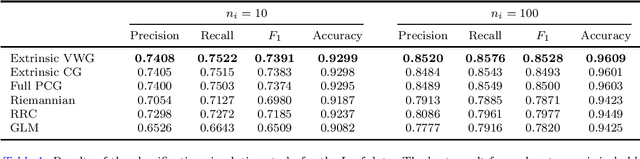
Kernel methods have had great success in the statistics and machine learning community. Despite their growing popularity, however, less effort has been drawn towards developing kernel based classification methods on manifold due to the non-Euclidean geometry. In this paper, motivated by the extrinsic framework of manifold-valued data analysis, we propose two types of new kernels on planar Kendall shape space $\Sigma_2^k$, called extrinsic Veronese Whitney Gaussian kernel and extrinsic complex Gaussian kernel. We show that our approach can be extended to develop Gaussian like kernels on any embedded manifold. Furthermore, kernel ridge regression classifier (KRRC) is implemented to address the shape classification problem on $\Sigma_2^k$, and their promising performances are illustrated through the real dataset.