Graph Canonical Correlation Analysis

Canonical correlation analysis (CCA) is a widely used technique for estimating associations between two sets of multi-dimensional variables. Recent advancements in CCA methods have expanded their application to decipher the interactions of multiomics datasets, imaging-omics datasets, and more. However, conventional CCA methods are limited in their ability to incorporate structured patterns in the cross-correlation matrix, potentially leading to suboptimal estimations. To address this limitation, we propose the graph Canonical Correlation Analysis (gCCA) approach, which calculates canonical correlations based on the graph structure of the cross-correlation matrix between the two sets of variables. We develop computationally efficient algorithms for gCCA, and provide theoretical results for finite sample analysis of best subset selection and canonical correlation estimation by introducing concentration inequalities and stopping time rule based on martingale theories. Extensive simulations demonstrate that gCCA outperforms competing CCA methods. Additionally, we apply gCCA to a multiomics dataset of DNA methylation and RNA-seq transcriptomics, identifying both positively and negatively regulated gene expression pathways by DNA methylation pathways.

Optimal Sampling Designs for Multi-dimensional Streaming Time Series with Application to Power Grid Sensor Data

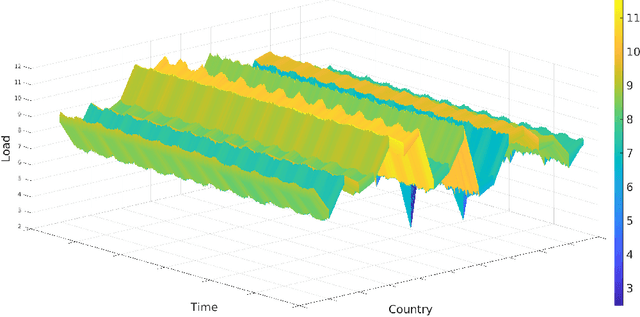
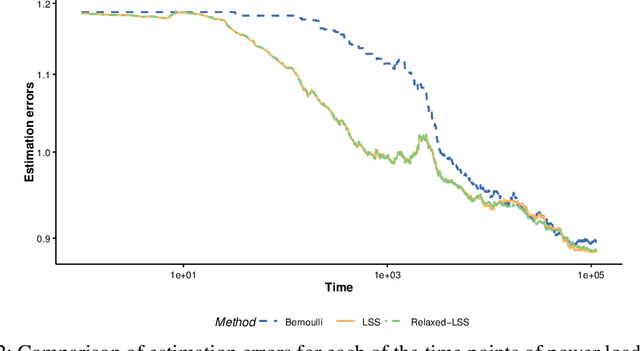
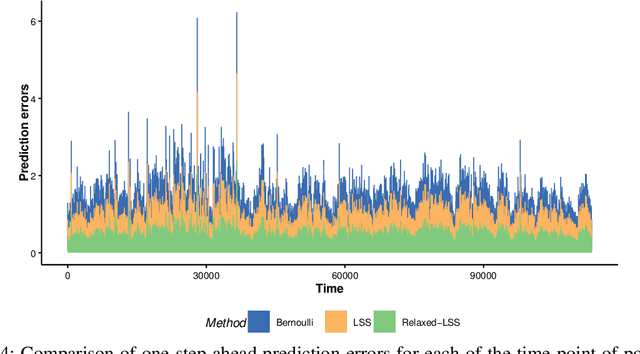
The Internet of Things (IoT) system generates massive high-speed temporally correlated streaming data and is often connected with online inference tasks under computational or energy constraints. Online analysis of these streaming time series data often faces a trade-off between statistical efficiency and computational cost. One important approach to balance this trade-off is sampling, where only a small portion of the sample is selected for the model fitting and update. Motivated by the demands of dynamic relationship analysis of IoT system, we study the data-dependent sample selection and online inference problem for a multi-dimensional streaming time series, aiming to provide low-cost real-time analysis of high-speed power grid electricity consumption data. Inspired by D-optimality criterion in design of experiments, we propose a class of online data reduction methods that achieve an optimal sampling criterion and improve the computational efficiency of the online analysis. We show that the optimal solution amounts to a strategy that is a mixture of Bernoulli sampling and leverage score sampling. The leverage score sampling involves auxiliary estimations that have a computational advantage over recursive least squares updates. Theoretical properties of the auxiliary estimations involved are also discussed. When applied to European power grid consumption data, the proposed leverage score based sampling methods outperform the benchmark sampling method in online estimation and prediction. The general applicability of the sampling-assisted online estimation method is assessed via simulation studies.