Knowledge Distillation and Dataset Distillation of Large Language Models: Emerging Trends, Challenges, and Future Directions

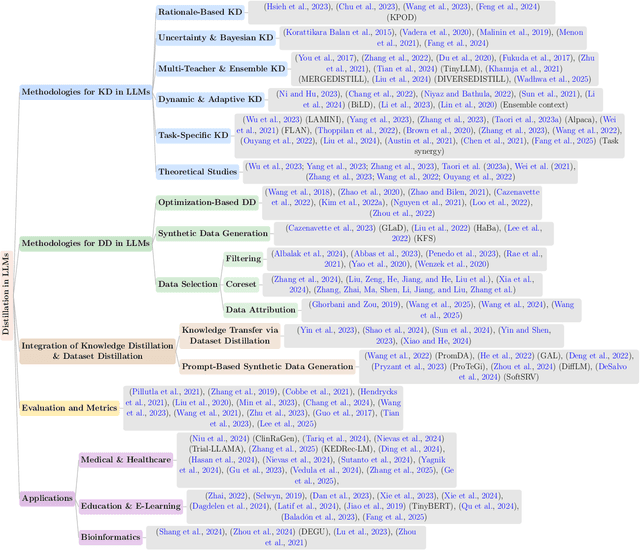
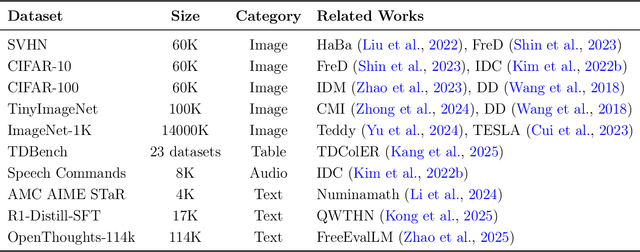
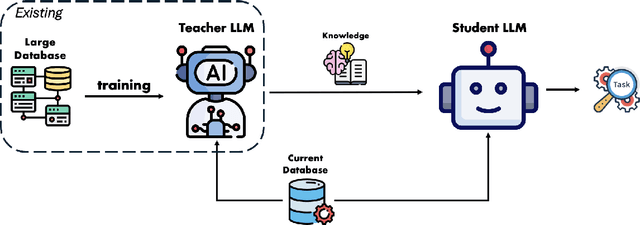
The exponential growth of Large Language Models (LLMs) continues to highlight the need for efficient strategies to meet ever-expanding computational and data demands. This survey provides a comprehensive analysis of two complementary paradigms: Knowledge Distillation (KD) and Dataset Distillation (DD), both aimed at compressing LLMs while preserving their advanced reasoning capabilities and linguistic diversity. We first examine key methodologies in KD, such as task-specific alignment, rationale-based training, and multi-teacher frameworks, alongside DD techniques that synthesize compact, high-impact datasets through optimization-based gradient matching, latent space regularization, and generative synthesis. Building on these foundations, we explore how integrating KD and DD can produce more effective and scalable compression strategies. Together, these approaches address persistent challenges in model scalability, architectural heterogeneity, and the preservation of emergent LLM abilities. We further highlight applications across domains such as healthcare and education, where distillation enables efficient deployment without sacrificing performance. Despite substantial progress, open challenges remain in preserving emergent reasoning and linguistic diversity, enabling efficient adaptation to continually evolving teacher models and datasets, and establishing comprehensive evaluation protocols. By synthesizing methodological innovations, theoretical foundations, and practical insights, our survey charts a path toward sustainable, resource-efficient LLMs through the tighter integration of KD and DD principles.

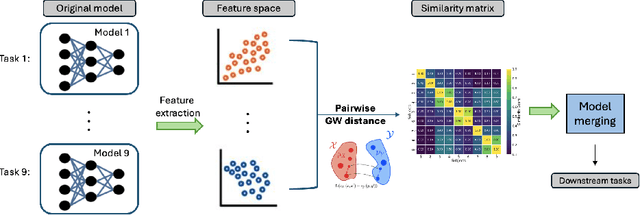
Efficient Multi-Task Inferencing: Model Merging with Gromov-Wasserstein Feature Alignment

Automatic scoring of student responses enhances efficiency in education, but deploying a separate neural network for each task increases storage demands, maintenance efforts, and redundant computations. To address these challenges, this paper introduces the Gromov-Wasserstein Scoring Model Merging (GW-SMM) method, which merges models based on feature distribution similarities measured via the Gromov-Wasserstein distance. Our approach begins by extracting features from student responses using individual models, capturing both item-specific context and unique learned representations. The Gromov-Wasserstein distance then quantifies the similarity between these feature distributions, identifying the most compatible models for merging. Models exhibiting the smallest pairwise distances, typically in pairs or trios, are merged by combining only the shared layers preceding the classification head. This strategy results in a unified feature extractor while preserving separate classification heads for item-specific scoring. We validated our approach against human expert knowledge and a GPT-o1-based merging method. GW-SMM consistently outperformed both, achieving a higher micro F1 score, macro F1 score, exact match accuracy, and per-label accuracy. The improvements in micro F1 and per-label accuracy were statistically significant compared to GPT-o1-based merging (p=0.04, p=0.01). Additionally, GW-SMM reduced storage requirements by half without compromising much accuracy, demonstrating its computational efficiency alongside reliable scoring performance.

Large Language Models for Bioinformatics

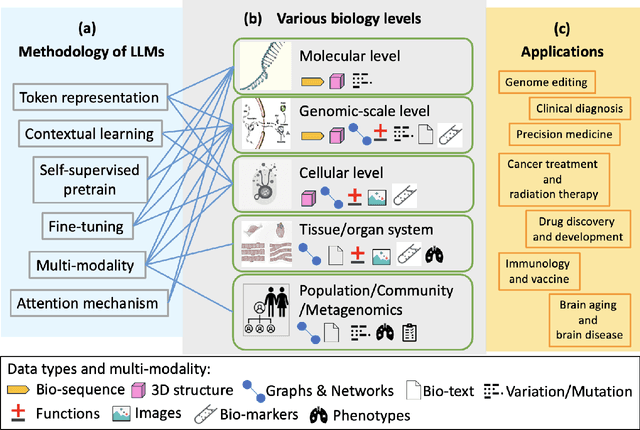
With the rapid advancements in large language model (LLM) technology and the emergence of bioinformatics-specific language models (BioLMs), there is a growing need for a comprehensive analysis of the current landscape, computational characteristics, and diverse applications. This survey aims to address this need by providing a thorough review of BioLMs, focusing on their evolution, classification, and distinguishing features, alongside a detailed examination of training methodologies, datasets, and evaluation frameworks. We explore the wide-ranging applications of BioLMs in critical areas such as disease diagnosis, drug discovery, and vaccine development, highlighting their impact and transformative potential in bioinformatics. We identify key challenges and limitations inherent in BioLMs, including data privacy and security concerns, interpretability issues, biases in training data and model outputs, and domain adaptation complexities. Finally, we highlight emerging trends and future directions, offering valuable insights to guide researchers and clinicians toward advancing BioLMs for increasingly sophisticated biological and clinical applications.

Non-Destructive Peat Analysis using Hyperspectral Imaging and Machine Learning

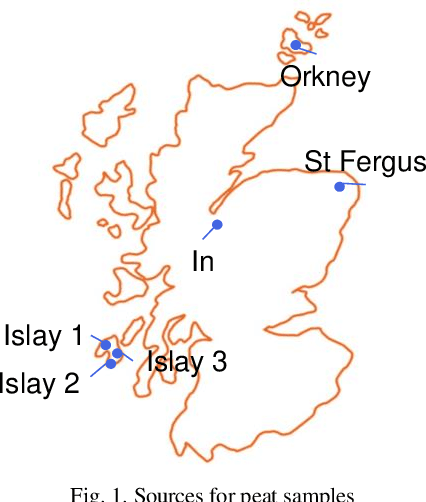
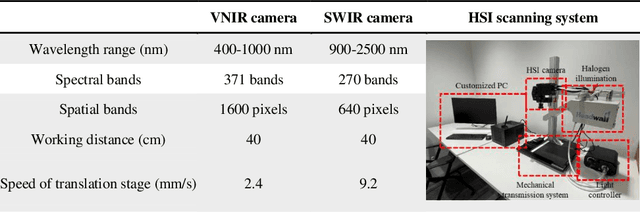
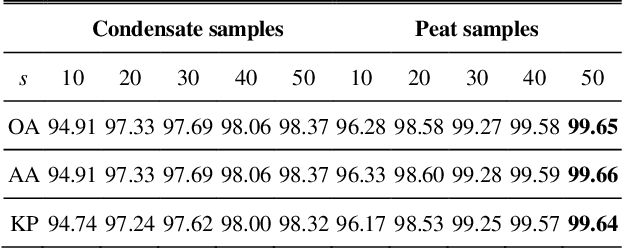
Peat, a crucial component in whisky production, imparts distinctive and irreplaceable flavours to the final product. However, the extraction of peat disrupts ancient ecosystems and releases significant amounts of carbon, contributing to climate change. This paper aims to address this issue by conducting a feasibility study on enhancing peat use efficiency in whisky manufacturing through non-destructive analysis using hyperspectral imaging. Results show that shot-wave infrared (SWIR) data is more effective for analyzing peat samples and predicting total phenol levels, with accuracies up to 99.81%.

Knowledge Distillation of LLM for Education

This study proposes a method for distilling the knowledge of fine-tuned Large Language Models (LLMs) into a smaller, more efficient, and accurate neural network, specifically targeting the challenge of deploying these models on resource-constrained devices. Our methodology involves training the smaller student model using the prediction probabilities of the LLM, which serves as a teacher model. This is achieved through a specialized loss function tailored to learn from the LLM's output probabilities, ensuring that the student model closely mimics the teacher's performance. To test this approach, we utilized a large dataset, 7T, containing 6,684 student-written responses to science questions and three other datasets with student-written responses. We also compared performance with original neural network (NN) models to validate the accuracy. Results have shown that the NN and distilled student models have comparable accuracy to the teacher model for the 7T dataset; however, other datasets have shown significantly lower accuracy (28% on average) for NN, though our proposed distilled model is still able to achieve 12\% higher accuracy than NN. Furthermore, the student model size ranges from 0.1M to 0.02M, 100 times smaller in terms of parameters and ten times smaller compared with the original output model size. The significance of this research lies in its potential to make advanced AI technologies accessible in typical educational settings, particularly for automatic scoring.

Optimal Sampling Designs for Multi-dimensional Streaming Time Series with Application to Power Grid Sensor Data

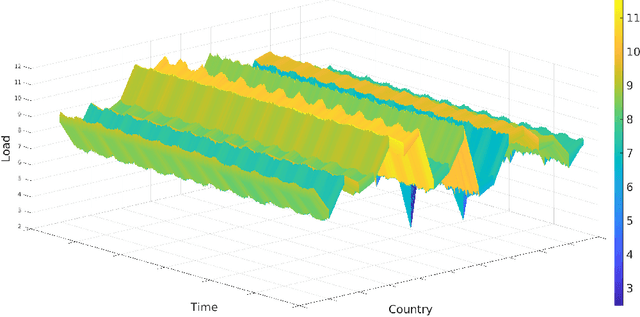
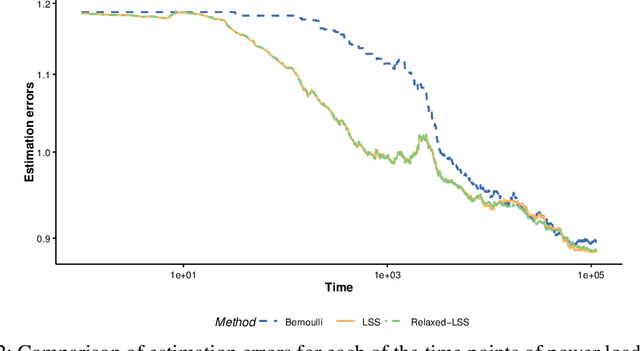
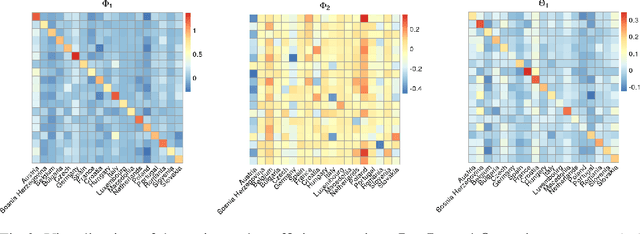
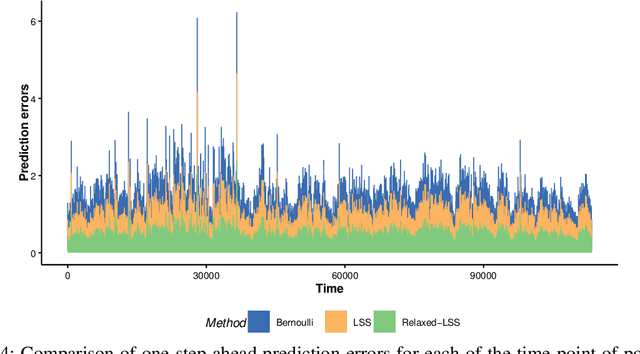
The Internet of Things (IoT) system generates massive high-speed temporally correlated streaming data and is often connected with online inference tasks under computational or energy constraints. Online analysis of these streaming time series data often faces a trade-off between statistical efficiency and computational cost. One important approach to balance this trade-off is sampling, where only a small portion of the sample is selected for the model fitting and update. Motivated by the demands of dynamic relationship analysis of IoT system, we study the data-dependent sample selection and online inference problem for a multi-dimensional streaming time series, aiming to provide low-cost real-time analysis of high-speed power grid electricity consumption data. Inspired by D-optimality criterion in design of experiments, we propose a class of online data reduction methods that achieve an optimal sampling criterion and improve the computational efficiency of the online analysis. We show that the optimal solution amounts to a strategy that is a mixture of Bernoulli sampling and leverage score sampling. The leverage score sampling involves auxiliary estimations that have a computational advantage over recursive least squares updates. Theoretical properties of the auxiliary estimations involved are also discussed. When applied to European power grid consumption data, the proposed leverage score based sampling methods outperform the benchmark sampling method in online estimation and prediction. The general applicability of the sampling-assisted online estimation method is assessed via simulation studies.

An optimal transport approach for selecting a representative subsample with application in efficient kernel density estimation

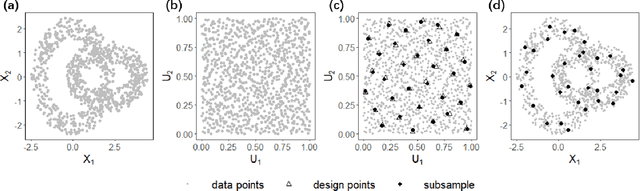
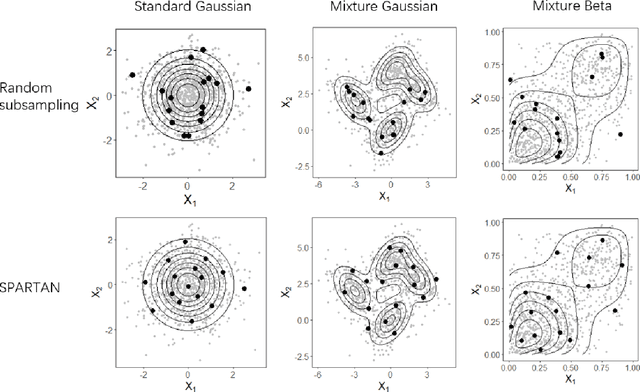
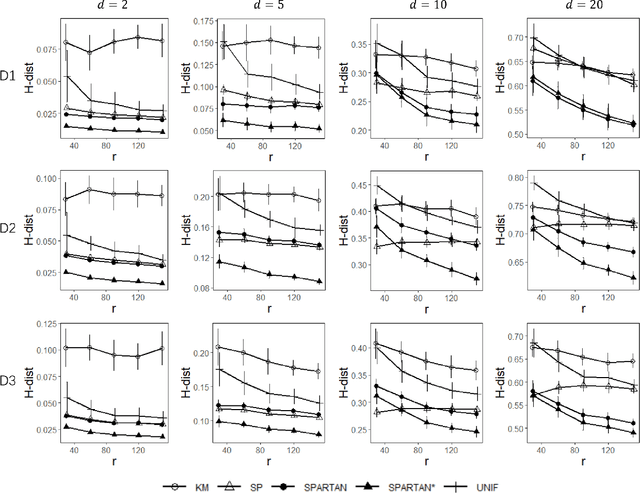
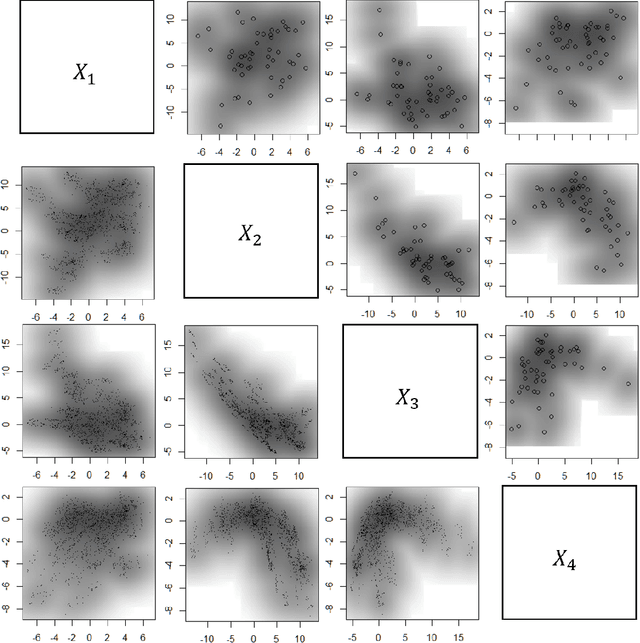
Subsampling methods aim to select a subsample as a surrogate for the observed sample. Such methods have been used pervasively in large-scale data analytics, active learning, and privacy-preserving analysis in recent decades. Instead of model-based methods, in this paper, we study model-free subsampling methods, which aim to identify a subsample that is not confined by model assumptions. Existing model-free subsampling methods are usually built upon clustering techniques or kernel tricks. Most of these methods suffer from either a large computational burden or a theoretical weakness. In particular, the theoretical weakness is that the empirical distribution of the selected subsample may not necessarily converge to the population distribution. Such computational and theoretical limitations hinder the broad applicability of model-free subsampling methods in practice. We propose a novel model-free subsampling method by utilizing optimal transport techniques. Moreover, we develop an efficient subsampling algorithm that is adaptive to the unknown probability density function. Theoretically, we show the selected subsample can be used for efficient density estimation by deriving the convergence rate for the proposed subsample kernel density estimator. We also provide the optimal bandwidth for the proposed estimator. Numerical studies on synthetic and real-world datasets demonstrate the performance of the proposed method is superior.

Managing dataset shift by adversarial validation for credit scoring

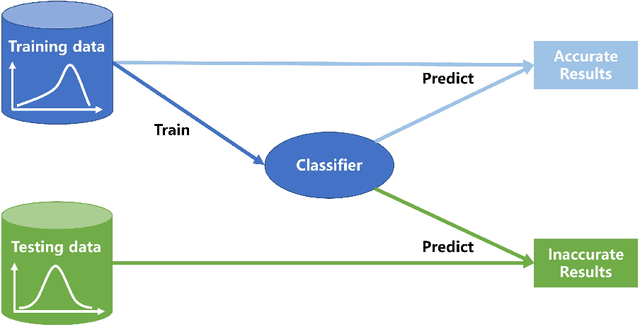
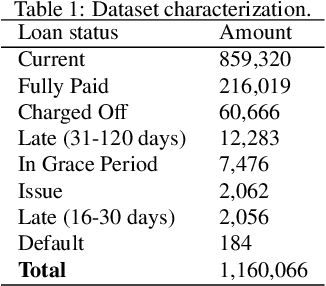
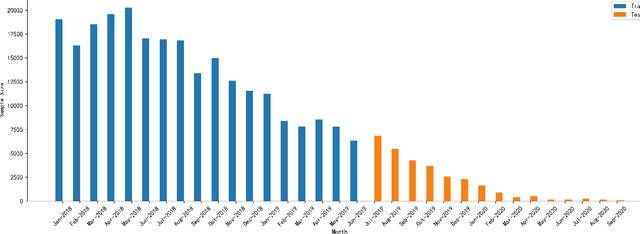
Dataset shift is common in credit scoring scenarios, and the inconsistency between the distribution of training data and the data that actually needs to be predicted is likely to cause poor model performance. However, most of the current studies do not take this into account, and they directly mix data from different time periods when training the models. This brings about two problems. Firstly, there is a risk of data leakage, i.e., using future data to predict the past. This can result in inflated results in offline validation, but unsatisfactory results in practical applications. Secondly, the macroeconomic environment and risk control strategies are likely to be different in different time periods, and the behavior patterns of borrowers may also change. The model trained with past data may not be applicable to the recent stage. Therefore, we propose a method based on adversarial validation to alleviate the dataset shift problem in credit scoring scenarios. In this method, partial training set samples with the closest distribution to the predicted data are selected for cross-validation by adversarial validation to ensure the generalization performance of the trained model on the predicted samples. In addition, through a simple splicing method, samples in the training data that are inconsistent with the test data distribution are also involved in the training process of cross-validation, which makes full use of all the data and further improves the model performance. To verify the effectiveness of the proposed method, comparative experiments with several other data split methods are conducted with the data provided by Lending Club. The experimental results demonstrate the importance of dataset shift in the field of credit scoring and the superiority of the proposed method.

Large-scale optimal transport map estimation using projection pursuit

This paper studies the estimation of large-scale optimal transport maps (OTM), which is a well-known challenging problem owing to the curse of dimensionality. Existing literature approximates the large-scale OTM by a series of one-dimensional OTM problems through iterative random projection. Such methods, however, suffer from slow or none convergence in practice due to the nature of randomly selected projection directions. Instead, we propose an estimation method of large-scale OTM by combining the idea of projection pursuit regression and sufficient dimension reduction. The proposed method, named projection pursuit Monge map (PPMM), adaptively selects the most ``informative'' projection direction in each iteration. We theoretically show the proposed dimension reduction method can consistently estimate the most ``informative'' projection direction in each iteration. Furthermore, the PPMM algorithm weakly convergences to the target large-scale OTM in a reasonable number of steps. Empirically, PPMM is computationally easy and converges fast. We assess its finite sample performance through the applications of Wasserstein distance estimation and generative models.

Sufficient dimension reduction for classification using principal optimal transport direction

Sufficient dimension reduction is used pervasively as a supervised dimension reduction approach. Most existing sufficient dimension reduction methods are developed for data with a continuous response and may have an unsatisfactory performance for the categorical response, especially for the binary-response. To address this issue, we propose a novel estimation method of sufficient dimension reduction subspace (SDR subspace) using optimal transport. The proposed method, named principal optimal transport direction (POTD), estimates the basis of the SDR subspace using the principal directions of the optimal transport coupling between the data respecting different response categories. The proposed method also reveals the relationship among three seemingly irrelevant topics, i.e., sufficient dimension reduction, support vector machine, and optimal transport. We study the asymptotic properties of POTD and show that in the cases when the class labels contain no error, POTD estimates the SDR subspace exclusively. Empirical studies show POTD outperforms most of the state-of-the-art linear dimension reduction methods.