Analysis of Multiscale Reinforcement Q-Learning Algorithms for Mean Field Control Games

Mean Field Control Games (MFCG), introduced in [Angiuli et al., 2022a], represent competitive games between a large number of large collaborative groups of agents in the infinite limit of number and size of groups. In this paper, we prove the convergence of a three-timescale Reinforcement Q-Learning (RL) algorithm to solve MFCG in a model-free approach from the point of view of representative agents. Our analysis uses a Q-table for finite state and action spaces updated at each discrete time-step over an infinite horizon. In [Angiuli et al., 2023], we proved convergence of two-timescale algorithms for MFG and MFC separately highlighting the need to follow multiple population distributions in the MFC case. Here, we integrate this feature for MFCG as well as three rates of update decreasing to zero in the proper ratios. Our technique of proof uses a generalization to three timescales of the two-timescale analysis in [Borkar, 1997]. We give a simple example satisfying the various hypothesis made in the proof of convergence and illustrating the performance of the algorithm.

An optimal transport approach for selecting a representative subsample with application in efficient kernel density estimation

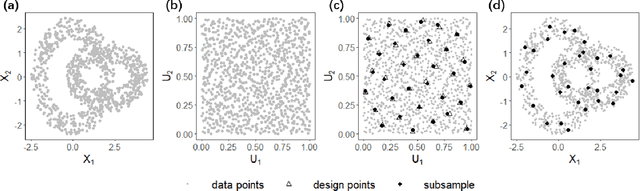
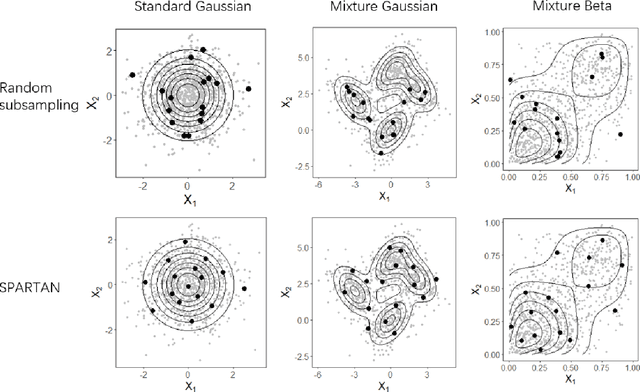
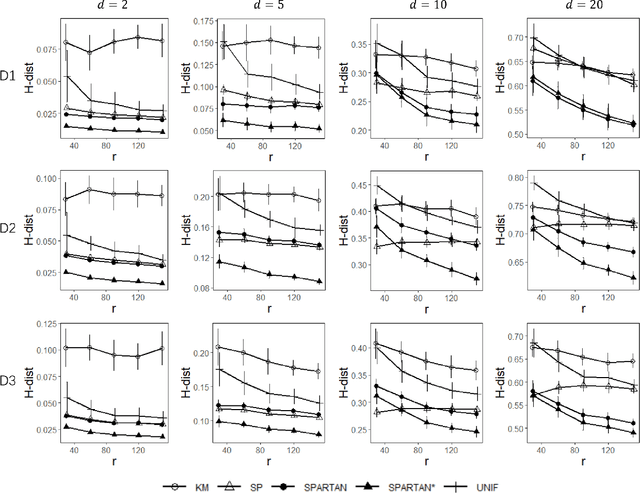
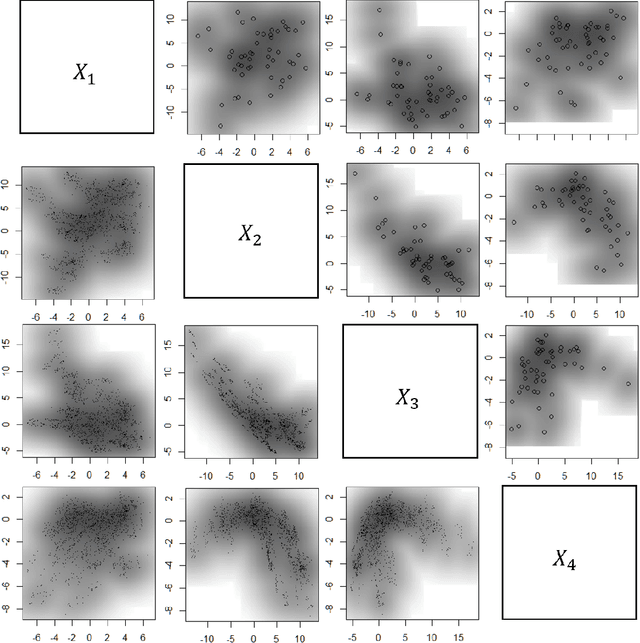
Subsampling methods aim to select a subsample as a surrogate for the observed sample. Such methods have been used pervasively in large-scale data analytics, active learning, and privacy-preserving analysis in recent decades. Instead of model-based methods, in this paper, we study model-free subsampling methods, which aim to identify a subsample that is not confined by model assumptions. Existing model-free subsampling methods are usually built upon clustering techniques or kernel tricks. Most of these methods suffer from either a large computational burden or a theoretical weakness. In particular, the theoretical weakness is that the empirical distribution of the selected subsample may not necessarily converge to the population distribution. Such computational and theoretical limitations hinder the broad applicability of model-free subsampling methods in practice. We propose a novel model-free subsampling method by utilizing optimal transport techniques. Moreover, we develop an efficient subsampling algorithm that is adaptive to the unknown probability density function. Theoretically, we show the selected subsample can be used for efficient density estimation by deriving the convergence rate for the proposed subsample kernel density estimator. We also provide the optimal bandwidth for the proposed estimator. Numerical studies on synthetic and real-world datasets demonstrate the performance of the proposed method is superior.

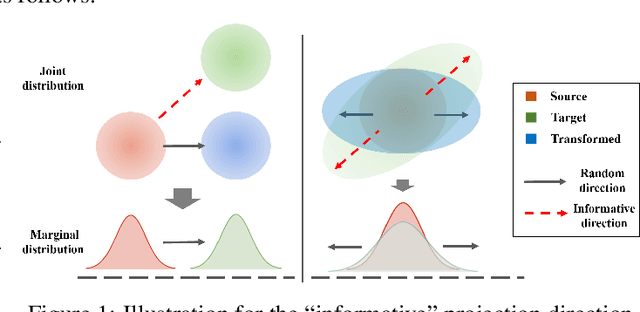
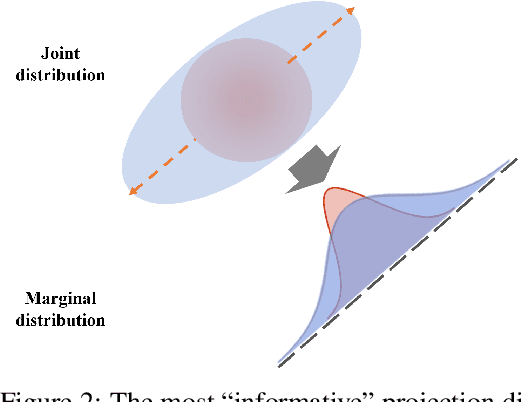
Large-scale optimal transport map estimation using projection pursuit

This paper studies the estimation of large-scale optimal transport maps (OTM), which is a well-known challenging problem owing to the curse of dimensionality. Existing literature approximates the large-scale OTM by a series of one-dimensional OTM problems through iterative random projection. Such methods, however, suffer from slow or none convergence in practice due to the nature of randomly selected projection directions. Instead, we propose an estimation method of large-scale OTM by combining the idea of projection pursuit regression and sufficient dimension reduction. The proposed method, named projection pursuit Monge map (PPMM), adaptively selects the most ``informative'' projection direction in each iteration. We theoretically show the proposed dimension reduction method can consistently estimate the most ``informative'' projection direction in each iteration. Furthermore, the PPMM algorithm weakly convergences to the target large-scale OTM in a reasonable number of steps. Empirically, PPMM is computationally easy and converges fast. We assess its finite sample performance through the applications of Wasserstein distance estimation and generative models.