A more efficient method for large-sample model-free feature screening via multi-armed bandits

We consider the model-free feature screening in large-scale ultrahigh-dimensional data analysis. Existing feature screening methods often face substantial computational challenges when dealing with large sample sizes. To alleviate the computational burden, we propose a rank-based model-free sure independence screening method (CR-SIS) and its efficient variant, BanditCR-SIS. The CR-SIS method, based on Chatterjee's rank correlation, is as straightforward to implement as the sure independence screening (SIS) method based on Pearson correlation introduced by Fan and Lv(2008), but it is significantly more powerful in detecting nonlinear relationships between variables. Motivated by the multi-armed bandit (MAB) problem, we reformulate the feature screening procedure to significantly reduce the computational complexity of CR-SIS. For a predictor matrix of size n \times p, the computational cost of CR-SIS is O(nlog(n)p), while BanditCR-SIS reduces this to O(\sqrt(n)log(n)p + nlog(n)). Theoretically, we establish the sure screening property for both CR-SIS and BanditCR-SIS under mild regularity conditions. Furthermore, we demonstrate the effectiveness of our methods through extensive experimental studies on both synthetic and real-world datasets. The results highlight their superior performance compared to classical screening methods, requiring significantly less computational time.

Gaussian Herding across Pens: An Optimal Transport Perspective on Global Gaussian Reduction for 3DGS

3D Gaussian Splatting (3DGS) has emerged as a powerful technique for radiance field rendering, but it typically requires millions of redundant Gaussian primitives, overwhelming memory and rendering budgets. Existing compaction approaches address this by pruning Gaussians based on heuristic importance scores, without global fidelity guarantee. To bridge this gap, we propose a novel optimal transport perspective that casts 3DGS compaction as global Gaussian mixture reduction. Specifically, we first minimize the composite transport divergence over a KD-tree partition to produce a compact geometric representation, and then decouple appearance from geometry by fine-tuning color and opacity attributes with far fewer Gaussian primitives. Experiments on benchmark datasets show that our method (i) yields negligible loss in rendering quality (PSNR, SSIM, LPIPS) compared to vanilla 3DGS with only 10% Gaussians; and (ii) consistently outperforms state-of-the-art 3DGS compaction techniques. Notably, our method is applicable to any stage of vanilla or accelerated 3DGS pipelines, providing an efficient and agnostic pathway to lightweight neural rendering.

Importance Sparsification for Sinkhorn Algorithm

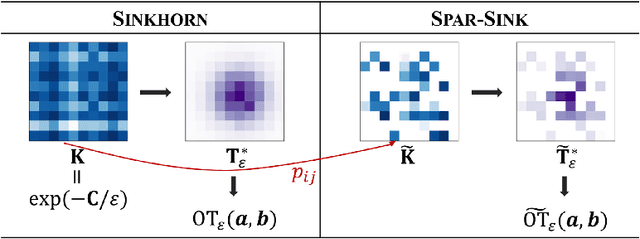
Sinkhorn algorithm has been used pervasively to approximate the solution to optimal transport (OT) and unbalanced optimal transport (UOT) problems. However, its practical application is limited due to the high computational complexity. To alleviate the computational burden, we propose a novel importance sparsification method, called Spar-Sink, to efficiently approximate entropy-regularized OT and UOT solutions. Specifically, our method employs natural upper bounds for unknown optimal transport plans to establish effective sampling probabilities, and constructs a sparse kernel matrix to accelerate Sinkhorn iterations, reducing the computational cost of each iteration from $O(n^2)$ to $\widetilde{O}(n)$ for a sample of size $n$. Theoretically, we show the proposed estimators for the regularized OT and UOT problems are consistent under mild regularity conditions. Experiments on various synthetic data demonstrate Spar-Sink outperforms mainstream competitors in terms of both estimation error and speed. A real-world echocardiogram data analysis shows Spar-Sink can effectively estimate and visualize cardiac cycles, from which one can identify heart failure and arrhythmia. To evaluate the numerical accuracy of cardiac cycle prediction, we consider the task of predicting the end-systole time point using the end-diastole one. Results show Spar-Sink performs as well as the classical Sinkhorn algorithm, requiring significantly less computational time.

Hilbert Curve Projection Distance for Distribution Comparison

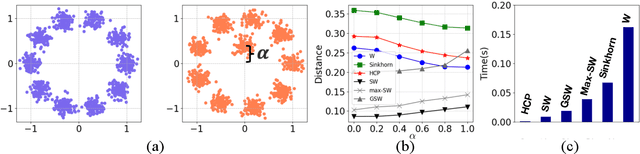
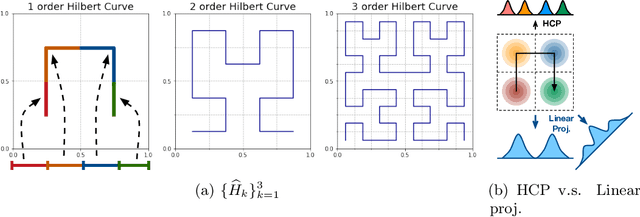
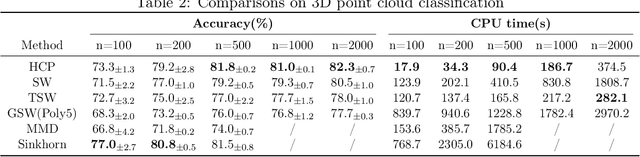
Distribution comparison plays a central role in many machine learning tasks like data classification and generative modeling. In this study, we propose a novel metric, called Hilbert curve projection (HCP) distance, to measure the distance between two probability distributions with high robustness and low complexity. In particular, we first project two high-dimensional probability densities using Hilbert curve to obtain a coupling between them, and then calculate the transport distance between these two densities in the original space, according to the coupling. We show that HCP distance is a proper metric and is well-defined for absolutely continuous probability measures. Furthermore, we demonstrate that the empirical HCP distance converges to its population counterpart at a rate of no more than $O(n^{-1/2d})$ under regularity conditions. To suppress the curse-of-dimensionality, we also develop two variants of the HCP distance using (learnable) subspace projections. Experiments on both synthetic and real-world data show that our HCP distance works as an effective surrogate of the Wasserstein distance with low complexity and overcomes the drawbacks of the sliced Wasserstein distance.

An optimal transport approach for selecting a representative subsample with application in efficient kernel density estimation

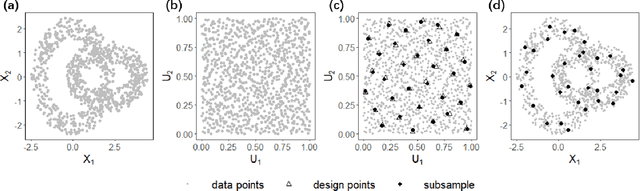
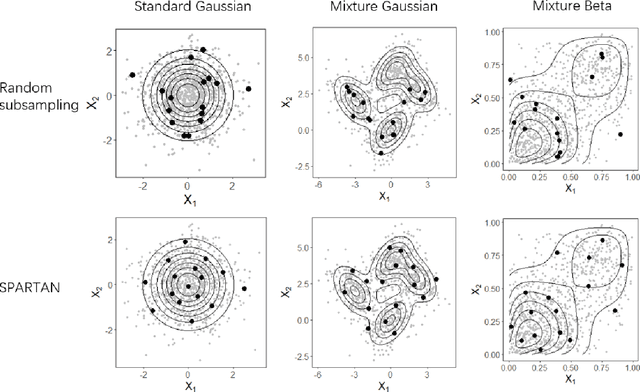
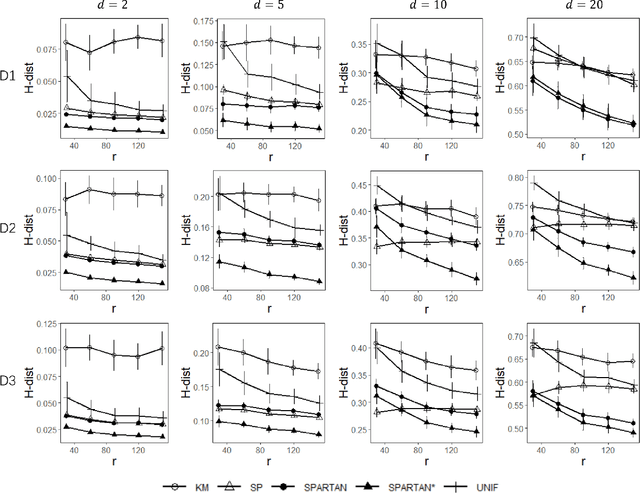
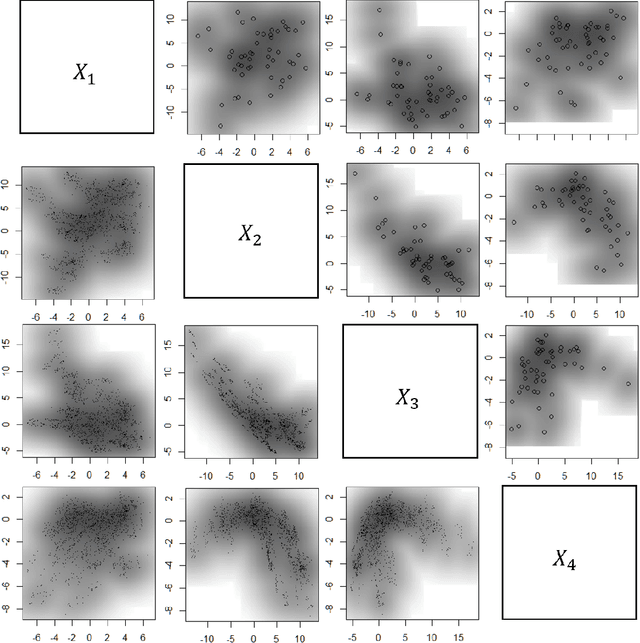
Subsampling methods aim to select a subsample as a surrogate for the observed sample. Such methods have been used pervasively in large-scale data analytics, active learning, and privacy-preserving analysis in recent decades. Instead of model-based methods, in this paper, we study model-free subsampling methods, which aim to identify a subsample that is not confined by model assumptions. Existing model-free subsampling methods are usually built upon clustering techniques or kernel tricks. Most of these methods suffer from either a large computational burden or a theoretical weakness. In particular, the theoretical weakness is that the empirical distribution of the selected subsample may not necessarily converge to the population distribution. Such computational and theoretical limitations hinder the broad applicability of model-free subsampling methods in practice. We propose a novel model-free subsampling method by utilizing optimal transport techniques. Moreover, we develop an efficient subsampling algorithm that is adaptive to the unknown probability density function. Theoretically, we show the selected subsample can be used for efficient density estimation by deriving the convergence rate for the proposed subsample kernel density estimator. We also provide the optimal bandwidth for the proposed estimator. Numerical studies on synthetic and real-world datasets demonstrate the performance of the proposed method is superior.

Efficient Approximation of Gromov-Wasserstein Distance using Importance Sparsification

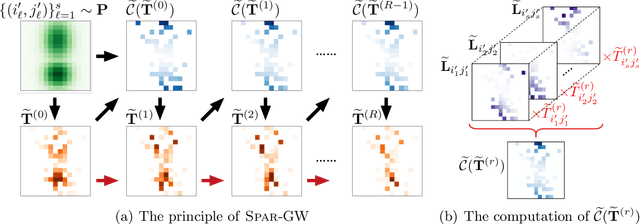
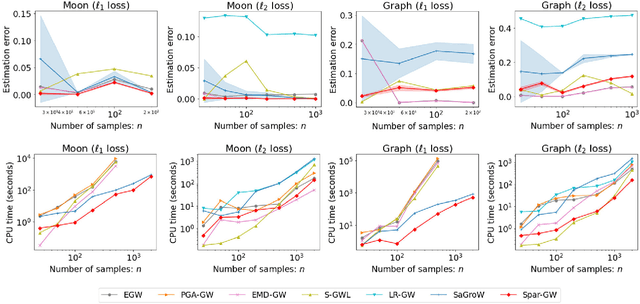
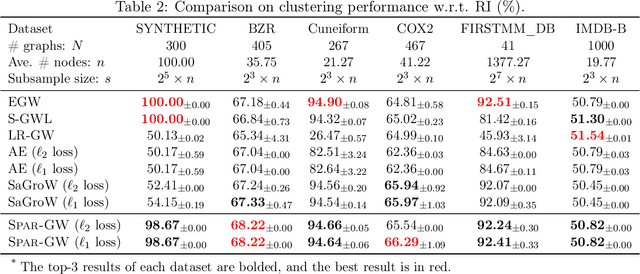
As a valid metric of metric-measure spaces, Gromov-Wasserstein (GW) distance has shown the potential for the matching problems of structured data like point clouds and graphs. However, its application in practice is limited due to its high computational complexity. To overcome this challenge, we propose a novel importance sparsification method, called Spar-GW, to approximate GW distance efficiently. In particular, instead of considering a dense coupling matrix, our method leverages a simple but effective sampling strategy to construct a sparse coupling matrix and update it with few computations. We demonstrate that the proposed Spar-GW method is applicable to the GW distance with arbitrary ground cost, and it reduces the complexity from $\mathcal{O}(n^4)$ to $\mathcal{O}(n^{2+\delta})$ for an arbitrary small $\delta>0$. In addition, this method can be extended to approximate the variants of GW distance, including the entropic GW distance, the fused GW distance, and the unbalanced GW distance. Experiments show the superiority of our Spar-GW to state-of-the-art methods in both synthetic and real-world tasks.

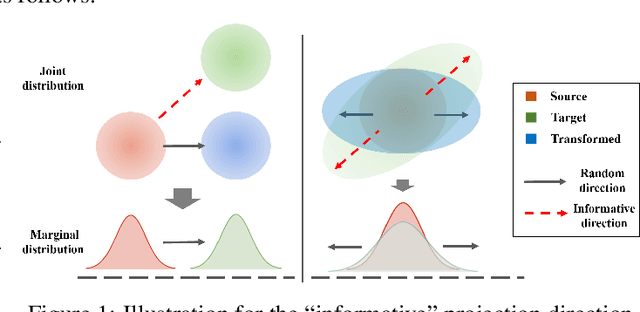
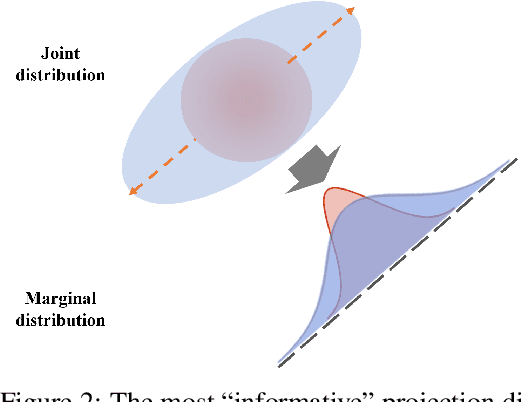
Large-scale optimal transport map estimation using projection pursuit

This paper studies the estimation of large-scale optimal transport maps (OTM), which is a well-known challenging problem owing to the curse of dimensionality. Existing literature approximates the large-scale OTM by a series of one-dimensional OTM problems through iterative random projection. Such methods, however, suffer from slow or none convergence in practice due to the nature of randomly selected projection directions. Instead, we propose an estimation method of large-scale OTM by combining the idea of projection pursuit regression and sufficient dimension reduction. The proposed method, named projection pursuit Monge map (PPMM), adaptively selects the most ``informative'' projection direction in each iteration. We theoretically show the proposed dimension reduction method can consistently estimate the most ``informative'' projection direction in each iteration. Furthermore, the PPMM algorithm weakly convergences to the target large-scale OTM in a reasonable number of steps. Empirically, PPMM is computationally easy and converges fast. We assess its finite sample performance through the applications of Wasserstein distance estimation and generative models.

Sufficient dimension reduction for classification using principal optimal transport direction

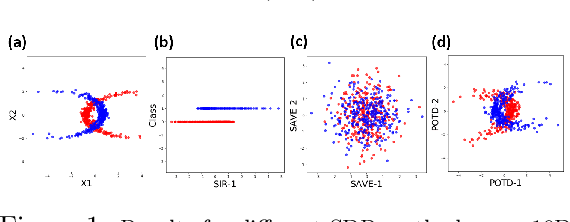
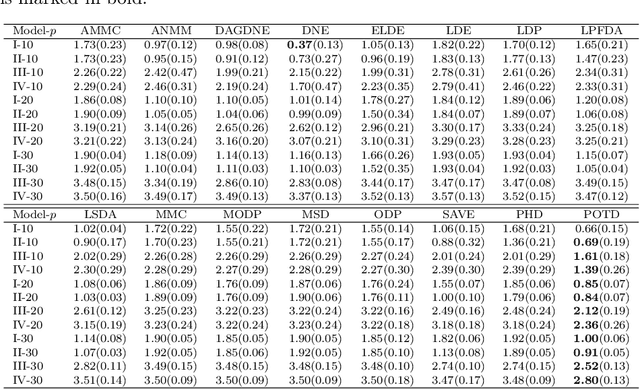
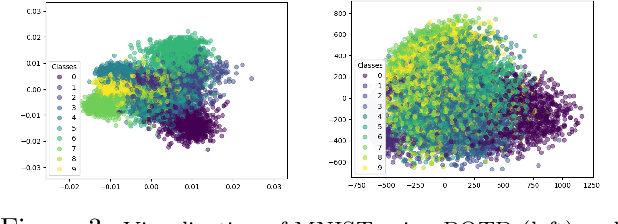
Sufficient dimension reduction is used pervasively as a supervised dimension reduction approach. Most existing sufficient dimension reduction methods are developed for data with a continuous response and may have an unsatisfactory performance for the categorical response, especially for the binary-response. To address this issue, we propose a novel estimation method of sufficient dimension reduction subspace (SDR subspace) using optimal transport. The proposed method, named principal optimal transport direction (POTD), estimates the basis of the SDR subspace using the principal directions of the optimal transport coupling between the data respecting different response categories. The proposed method also reveals the relationship among three seemingly irrelevant topics, i.e., sufficient dimension reduction, support vector machine, and optimal transport. We study the asymptotic properties of POTD and show that in the cases when the class labels contain no error, POTD estimates the SDR subspace exclusively. Empirical studies show POTD outperforms most of the state-of-the-art linear dimension reduction methods.