Hilbert Curve Projection Distance for Distribution Comparison
Paper and Code
Jun 09, 2022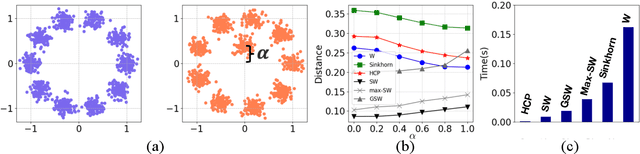

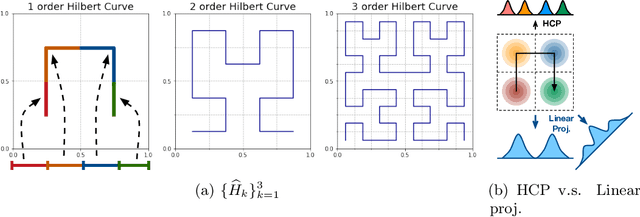
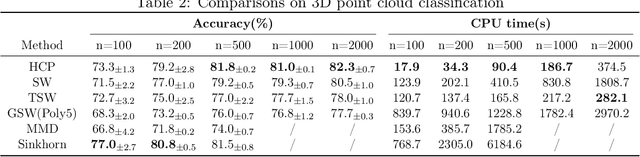
Distribution comparison plays a central role in many machine learning tasks like data classification and generative modeling. In this study, we propose a novel metric, called Hilbert curve projection (HCP) distance, to measure the distance between two probability distributions with high robustness and low complexity. In particular, we first project two high-dimensional probability densities using Hilbert curve to obtain a coupling between them, and then calculate the transport distance between these two densities in the original space, according to the coupling. We show that HCP distance is a proper metric and is well-defined for absolutely continuous probability measures. Furthermore, we demonstrate that the empirical HCP distance converges to its population counterpart at a rate of no more than $O(n^{-1/2d})$ under regularity conditions. To suppress the curse-of-dimensionality, we also develop two variants of the HCP distance using (learnable) subspace projections. Experiments on both synthetic and real-world data show that our HCP distance works as an effective surrogate of the Wasserstein distance with low complexity and overcomes the drawbacks of the sliced Wasserstein distance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge