Knowledge Distillation and Dataset Distillation of Large Language Models: Emerging Trends, Challenges, and Future Directions

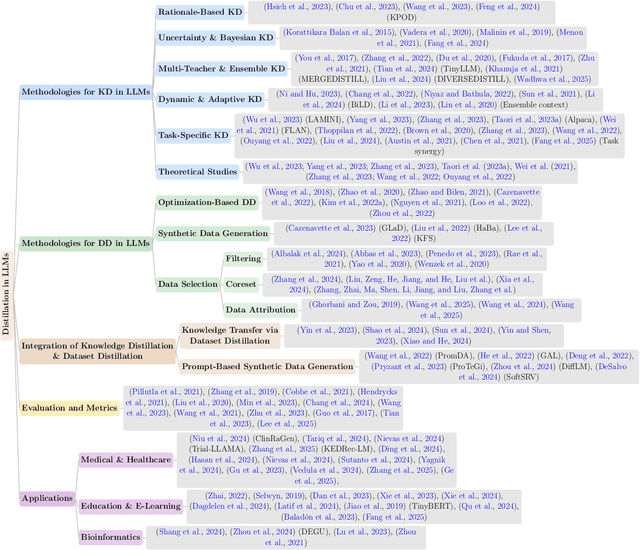
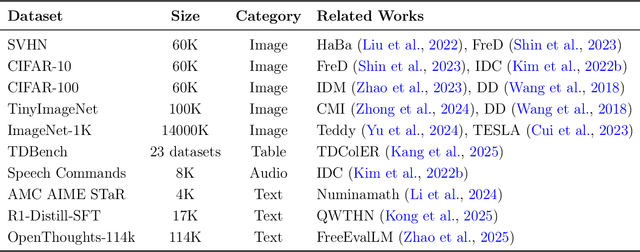
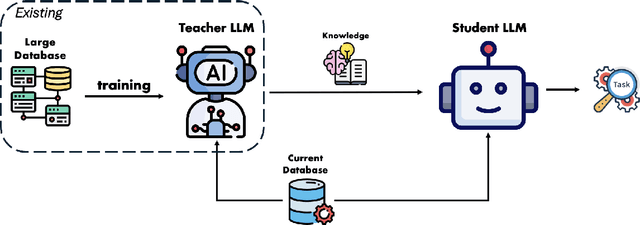
The exponential growth of Large Language Models (LLMs) continues to highlight the need for efficient strategies to meet ever-expanding computational and data demands. This survey provides a comprehensive analysis of two complementary paradigms: Knowledge Distillation (KD) and Dataset Distillation (DD), both aimed at compressing LLMs while preserving their advanced reasoning capabilities and linguistic diversity. We first examine key methodologies in KD, such as task-specific alignment, rationale-based training, and multi-teacher frameworks, alongside DD techniques that synthesize compact, high-impact datasets through optimization-based gradient matching, latent space regularization, and generative synthesis. Building on these foundations, we explore how integrating KD and DD can produce more effective and scalable compression strategies. Together, these approaches address persistent challenges in model scalability, architectural heterogeneity, and the preservation of emergent LLM abilities. We further highlight applications across domains such as healthcare and education, where distillation enables efficient deployment without sacrificing performance. Despite substantial progress, open challenges remain in preserving emergent reasoning and linguistic diversity, enabling efficient adaptation to continually evolving teacher models and datasets, and establishing comprehensive evaluation protocols. By synthesizing methodological innovations, theoretical foundations, and practical insights, our survey charts a path toward sustainable, resource-efficient LLMs through the tighter integration of KD and DD principles.

Large Language Models for Bioinformatics

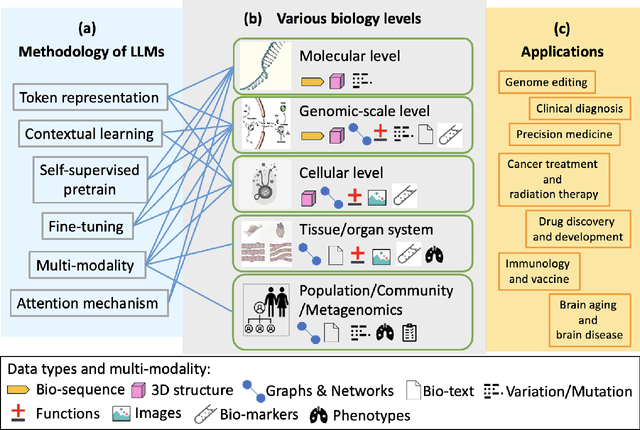
With the rapid advancements in large language model (LLM) technology and the emergence of bioinformatics-specific language models (BioLMs), there is a growing need for a comprehensive analysis of the current landscape, computational characteristics, and diverse applications. This survey aims to address this need by providing a thorough review of BioLMs, focusing on their evolution, classification, and distinguishing features, alongside a detailed examination of training methodologies, datasets, and evaluation frameworks. We explore the wide-ranging applications of BioLMs in critical areas such as disease diagnosis, drug discovery, and vaccine development, highlighting their impact and transformative potential in bioinformatics. We identify key challenges and limitations inherent in BioLMs, including data privacy and security concerns, interpretability issues, biases in training data and model outputs, and domain adaptation complexities. Finally, we highlight emerging trends and future directions, offering valuable insights to guide researchers and clinicians toward advancing BioLMs for increasingly sophisticated biological and clinical applications.

An optimal transport approach for selecting a representative subsample with application in efficient kernel density estimation

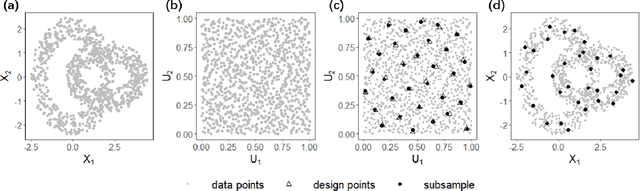
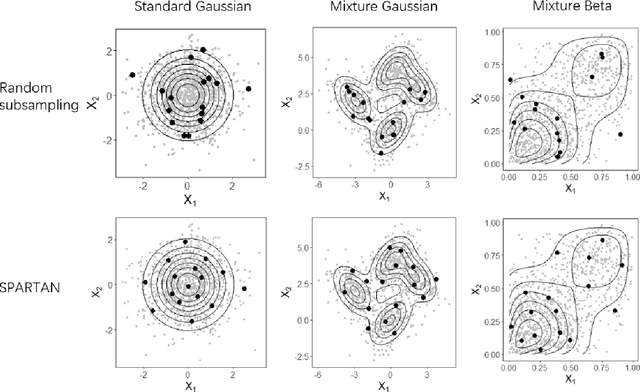
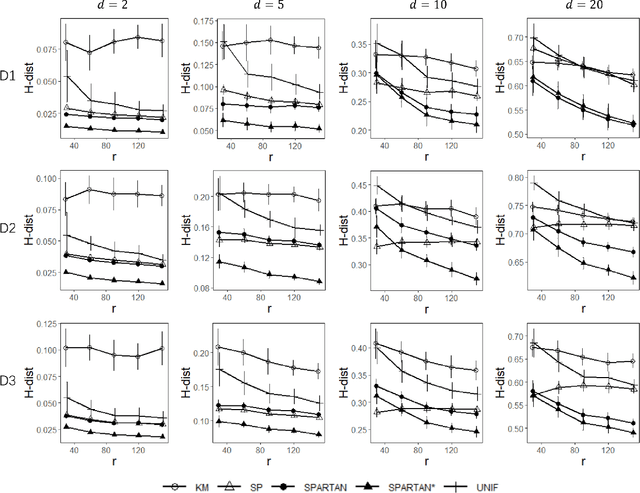
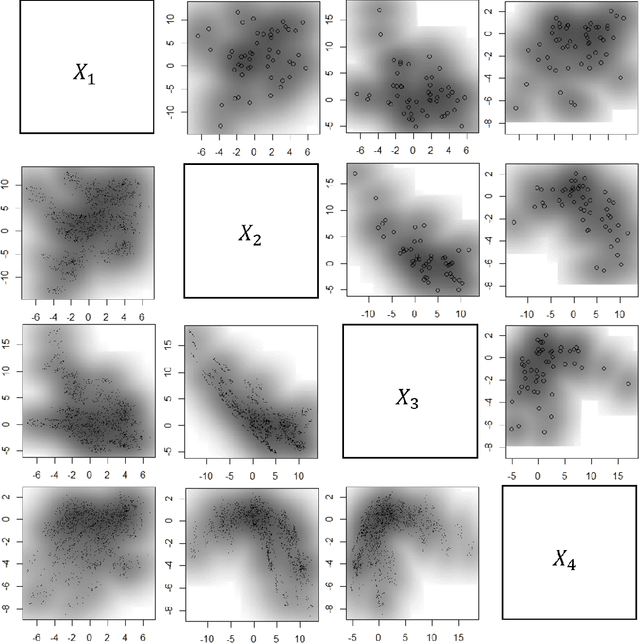
Subsampling methods aim to select a subsample as a surrogate for the observed sample. Such methods have been used pervasively in large-scale data analytics, active learning, and privacy-preserving analysis in recent decades. Instead of model-based methods, in this paper, we study model-free subsampling methods, which aim to identify a subsample that is not confined by model assumptions. Existing model-free subsampling methods are usually built upon clustering techniques or kernel tricks. Most of these methods suffer from either a large computational burden or a theoretical weakness. In particular, the theoretical weakness is that the empirical distribution of the selected subsample may not necessarily converge to the population distribution. Such computational and theoretical limitations hinder the broad applicability of model-free subsampling methods in practice. We propose a novel model-free subsampling method by utilizing optimal transport techniques. Moreover, we develop an efficient subsampling algorithm that is adaptive to the unknown probability density function. Theoretically, we show the selected subsample can be used for efficient density estimation by deriving the convergence rate for the proposed subsample kernel density estimator. We also provide the optimal bandwidth for the proposed estimator. Numerical studies on synthetic and real-world datasets demonstrate the performance of the proposed method is superior.

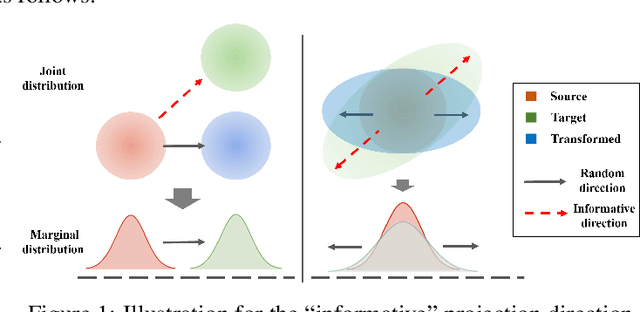
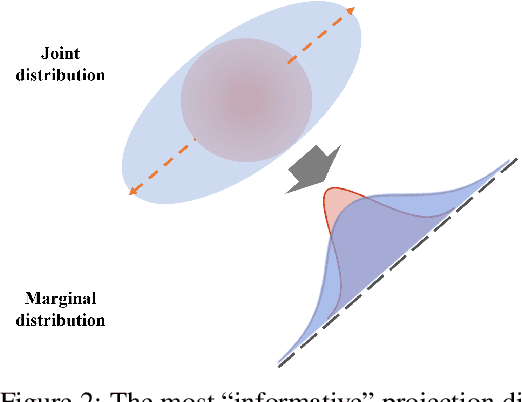
Large-scale optimal transport map estimation using projection pursuit

This paper studies the estimation of large-scale optimal transport maps (OTM), which is a well-known challenging problem owing to the curse of dimensionality. Existing literature approximates the large-scale OTM by a series of one-dimensional OTM problems through iterative random projection. Such methods, however, suffer from slow or none convergence in practice due to the nature of randomly selected projection directions. Instead, we propose an estimation method of large-scale OTM by combining the idea of projection pursuit regression and sufficient dimension reduction. The proposed method, named projection pursuit Monge map (PPMM), adaptively selects the most ``informative'' projection direction in each iteration. We theoretically show the proposed dimension reduction method can consistently estimate the most ``informative'' projection direction in each iteration. Furthermore, the PPMM algorithm weakly convergences to the target large-scale OTM in a reasonable number of steps. Empirically, PPMM is computationally easy and converges fast. We assess its finite sample performance through the applications of Wasserstein distance estimation and generative models.

Ensemble machine learning approach for screening of coronary heart disease based on echocardiography and risk factors

Background: Extensive clinical evidence suggests that a preventive screening of coronary heart disease (CHD) at an earlier stage can greatly reduce the mortality rate. We use 64 two-dimensional speckle tracking echocardiography (2D-STE) features and seven clinical features to predict whether one has CHD. Methods: We develop a machine learning approach that integrates a number of popular classification methods together by model stacking, and generalize the traditional stacking method to a two-step stacking method to improve the diagnostic performance. Results: By borrowing strengths from multiple classification models through the proposed method, we improve the CHD classification accuracy from around 70% to 87.7% on the testing set. The sensitivity of the proposed method is 0.903 and the specificity is 0.843, with an AUC of 0.904, which is significantly higher than those of the individual classification models. Conclusions: Our work lays a foundation for the deployment of speckle tracking echocardiography-based screening tools for coronary heart disease.

Sufficient dimension reduction for classification using principal optimal transport direction

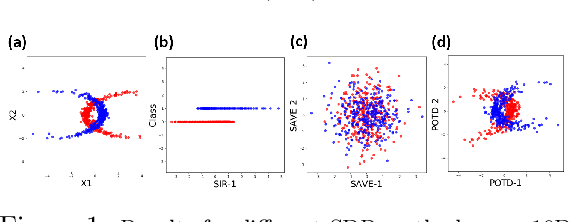
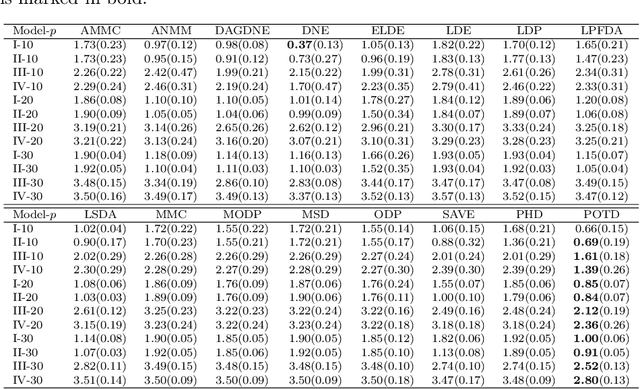
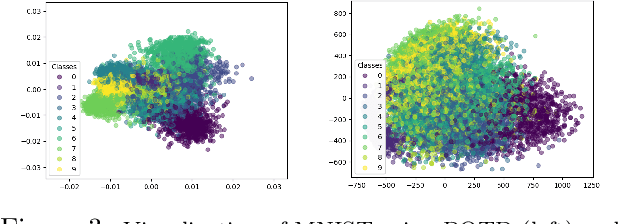
Sufficient dimension reduction is used pervasively as a supervised dimension reduction approach. Most existing sufficient dimension reduction methods are developed for data with a continuous response and may have an unsatisfactory performance for the categorical response, especially for the binary-response. To address this issue, we propose a novel estimation method of sufficient dimension reduction subspace (SDR subspace) using optimal transport. The proposed method, named principal optimal transport direction (POTD), estimates the basis of the SDR subspace using the principal directions of the optimal transport coupling between the data respecting different response categories. The proposed method also reveals the relationship among three seemingly irrelevant topics, i.e., sufficient dimension reduction, support vector machine, and optimal transport. We study the asymptotic properties of POTD and show that in the cases when the class labels contain no error, POTD estimates the SDR subspace exclusively. Empirical studies show POTD outperforms most of the state-of-the-art linear dimension reduction methods.

A Review on Modern Computational Optimal Transport Methods with Applications in Biomedical Research

Optimal transport has been one of the most exciting subjects in mathematics, starting from the 18th century. As a powerful tool to transport between two probability measures, optimal transport methods have been reinvigorated nowadays in a remarkable proliferation of modern data science applications. To meet the big data challenges, various computational tools have been developed in the recent decade to accelerate the computation for optimal transport methods. In this review, we present some cutting-edge computational optimal transport methods with a focus on the regularization-based methods and the projection-based methods. We discuss their real-world applications in biomedical research.

Minimax Nonparametric Two-sample Test

We consider the problem of comparing probability densities between two groups. To model the complex pattern of the underlying densities, we formulate the problem as a nonparametric density hypothesis testing problem. The major difficulty is that conventional tests may fail to distinguish the alternative from the null hypothesis under the controlled type I error. In this paper, we model log-transformed densities in a tensor product reproducing kernel Hilbert space (RKHS) and propose a probabilistic decomposition of this space. Under such a decomposition, we quantify the difference of the densities between two groups by the component norm in the probabilistic decomposition. Based on the Bernstein width, a sharp minimax lower bound of the distinguishable rate is established for the nonparametric two-sample test. We then propose a penalized likelihood ratio (PLR) test possessing the Wilks' phenomenon with an asymptotically Chi-square distributed test statistic and achieving the established minimax testing rate. Simulations and real applications demonstrate that the proposed test outperforms the conventional approaches under various scenarios.