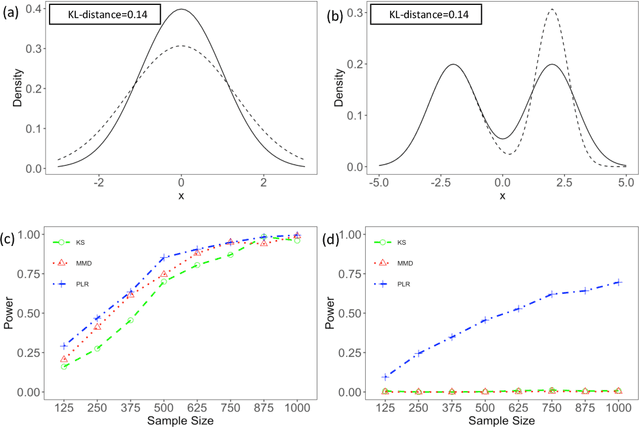
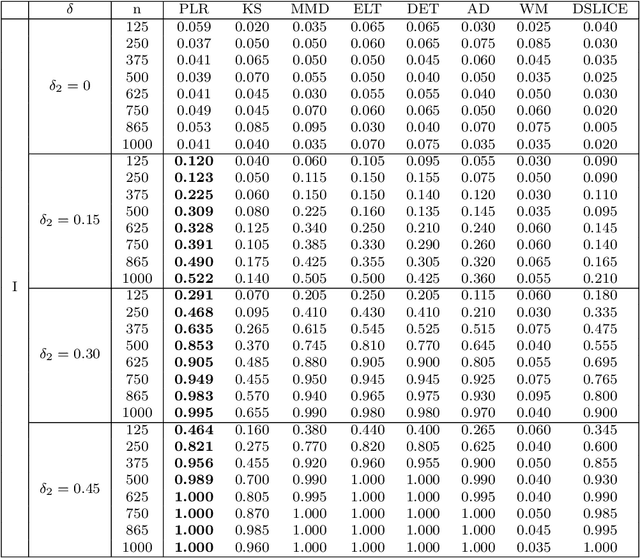
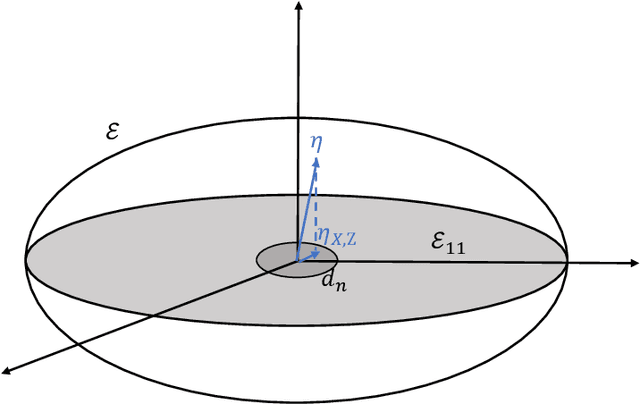
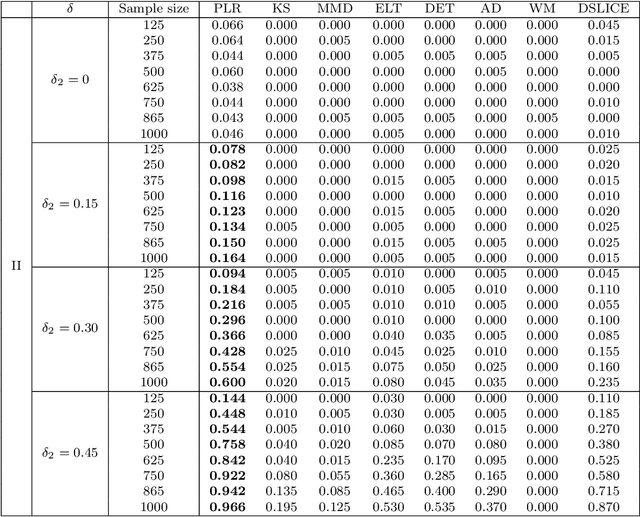
Minimax Nonparametric Two-sample Test

We consider the problem of comparing probability densities between two groups. To model the complex pattern of the underlying densities, we formulate the problem as a nonparametric density hypothesis testing problem. The major difficulty is that conventional tests may fail to distinguish the alternative from the null hypothesis under the controlled type I error. In this paper, we model log-transformed densities in a tensor product reproducing kernel Hilbert space (RKHS) and propose a probabilistic decomposition of this space. Under such a decomposition, we quantify the difference of the densities between two groups by the component norm in the probabilistic decomposition. Based on the Bernstein width, a sharp minimax lower bound of the distinguishable rate is established for the nonparametric two-sample test. We then propose a penalized likelihood ratio (PLR) test possessing the Wilks' phenomenon with an asymptotically Chi-square distributed test statistic and achieving the established minimax testing rate. Simulations and real applications demonstrate that the proposed test outperforms the conventional approaches under various scenarios.

Statistical Estimation of Malware Detection Metrics in the Absence of Ground Truth

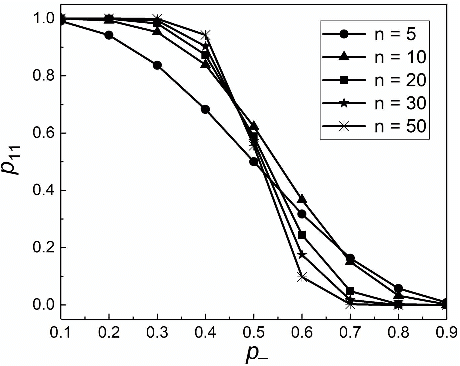
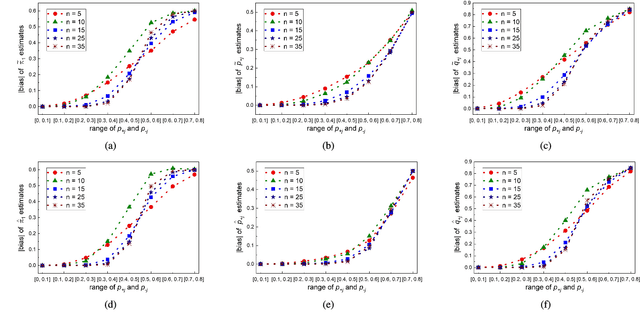
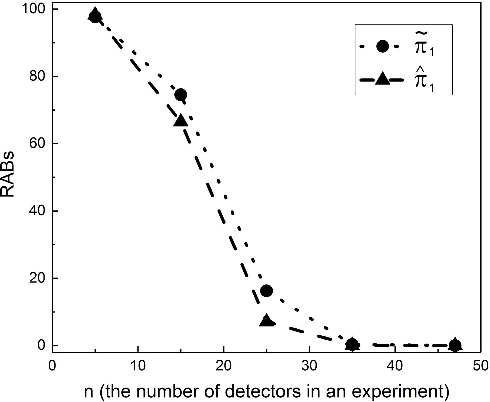
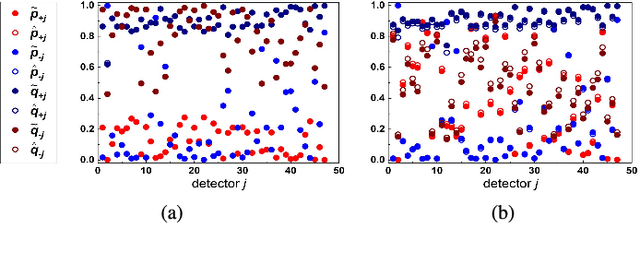
The accurate measurement of security metrics is a critical research problem because an improper or inaccurate measurement process can ruin the usefulness of the metrics, no matter how well they are defined. This is a highly challenging problem particularly when the ground truth is unknown or noisy. In contrast to the well perceived importance of defining security metrics, the measurement of security metrics has been little understood in the literature. In this paper, we measure five malware detection metrics in the {\em absence} of ground truth, which is a realistic setting that imposes many technical challenges. The ultimate goal is to develop principled, automated methods for measuring these metrics at the maximum accuracy possible. The problem naturally calls for investigations into statistical estimators by casting the measurement problem as a {\em statistical estimation} problem. We propose statistical estimators for these five malware detection metrics. By investigating the statistical properties of these estimators, we are able to characterize when the estimators are accurate, and what adjustments can be made to improve them under what circumstances. We use synthetic data with known ground truth to validate these statistical estimators. Then, we employ these estimators to measure five metrics with respect to a large dataset collected from VirusTotal. We believe our study touches upon a vital problem that has not been paid due attention and will inspire many future investigations.